complexe functies


Complexe functies.	© h.hofstede (h.hofstede@hogeland.nl)

Een functie was tot nu toe, bij de reële getallen, een soort recept om aan x-getallen (het domein) y-getallen te koppelen. Het is een formule waar je een x instopt en waar dan een y uit komt rollen. We schreven dat meestal als y = f(x). We konden er een grafiek van maken met een x-as en een y-as.

Hoe is dat bij de complexe getallen?

Nou precies zo. Een functie is ook een soort voorschrift waar je een complex getal z instopt en waar dan een ander complex getal uitkomt. Niks aan de hand zou je zeggen. Het probleem komt pas bij het tekenen van een grafiek.....

Wat je in de functie stopt zijn complexe getallen en die liggen niet netjes op een x-as, maar in een heel vlak. En ook wat er uitkomt zijn complexe getallen die dus ook in een vlak liggen, en niet netjes op een y-as of zo. Daarom kun je niet zomaar een grafiek tekenen. Als "x-as" zou je een heel vlak nodig hebben en als "y-as" ook! Dat zou een vierdimensionale tekening geven. En dat kunnen we helaas niet....

Meestal tekenen we daarom twee vlakken naast elkaar. Eentje voor de getallen die in de functie worden gestopt (het domein, en eentje voor de getallen die er uitkomen. Dat zijn dus twee complexe vlakken naast elkaar. In het eerste vlak tekenen we dan bijvoorbeeld figuren als rechte lijnen of cirkels of rechthoeken, en in het tweede vlak teken we waar die figuren terechtkomen als we de functie erop toepassen. Zo hopen we een beetje een beeld te krijgen van wat de functie "doet".

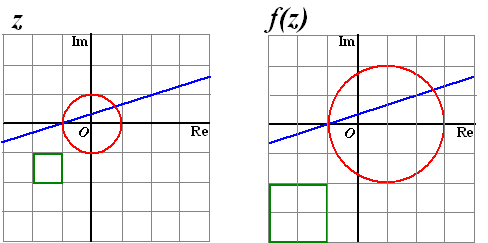
Neem bijvoorbeeld de functie f(z) = 2z + 1
Daar zou de volgende "tekening" bij kunnen horen:

Links staan de originelen, rechts de beelden daarvan bij de functie f(z) = 2z + 1. Door veel van deze vormen te bekijken krijg je misschien een beetje een idee van wat deze functie doet. Probeer dat maar eens in je eigen woorden te omschrijven aan de hand van deze plaatjes. Lastig hé? Misschien gaat het met de formule wel makkelijker dan met de plaatjes. Hieronder staat wat er ongeveer gebeurt. Denk eerst zelf na!!!!

eerst wordt de afstand van elk punt tot O verdubbeld
daarna schuift het geheel 1 naar rechts

Het is nogal behelpen zo! Stel dat we voor de reële functie f(x) = 2x + 1 ook de x-as en de y-as apart zouden tekenen, met gekleurde gebiedjes en hun beeld. Dat zou zóiets kunnen opleveren:

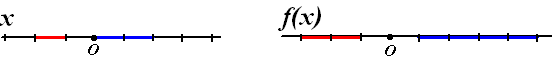Eigenlijk heb je geen idee wat hier nou gebeurt.
Het is in ieder geval lang niet zo duidelijk als die mooie lineaire grafiek van y = 2x + 1 die we gewend waren....

Jammer.
We moeten er maar het beste van maken, en proberen een beetje te snappen wat die complexe functies nou precies doen.
Dat vergt vast een boel oefening......

De "lineaire" functie: f(z) = (a + bi) • z + (c + di)

Dat was de simpelste die ik kon verzinnen.
Maar hij is helemaal niet simpel!!!!
Wat gebeurt er met een punt z bij deze functie? Waar komt het beeld van z terecht?
Dat is in twee etappes te zien:

Als je een getal z vermenigvuldigt met a + bi = r • (cosφ + isinφ) dan is dat een draaivermenigvuldiging. Dat betekent in het complexe vlak dat de afstand (van het punt dat bij z hoort) tot de oorsprong r keer zo groot wordt, en dat het punt daarna over een hoek j wordt gedraaid.

Als je bij een getal z een vast getal c + di optelt dan is dat een verschuiving. In het complexe vlak gaat zo'n punt dan c naar rechts en d omhoog.

Daarmee kun je aardig zien hoe het beeld van een figuur/gebied eruit gaat zien.
Het is handig dat je het volgende daarbij onthoudt:

"rechte lijnen blijven rechte lijnen"
"cirkels blijven cirkels"

Immers bij al die "bewerkingen" in de punten I en II hierboven blijven rechte lijnen nog steeds rechte lijnen en cirkels blijven cirkels. Het handige daaraan is dat je bijvoorbeeld, om het beeld van een driehoek te vinden, alleen maar hoeft te kijken waar de hoekpunten terecht komen; dan heb je de hoekpunten van de beelddriehoek. De rechte lijnen daartussen blijven rechte lijnen. En om het beeld van een deel van een cirkel te vinden hoef je alleen maar te kijken waar het middelpunt en waar de uiteinden terechtkomen.

OPGAVEN

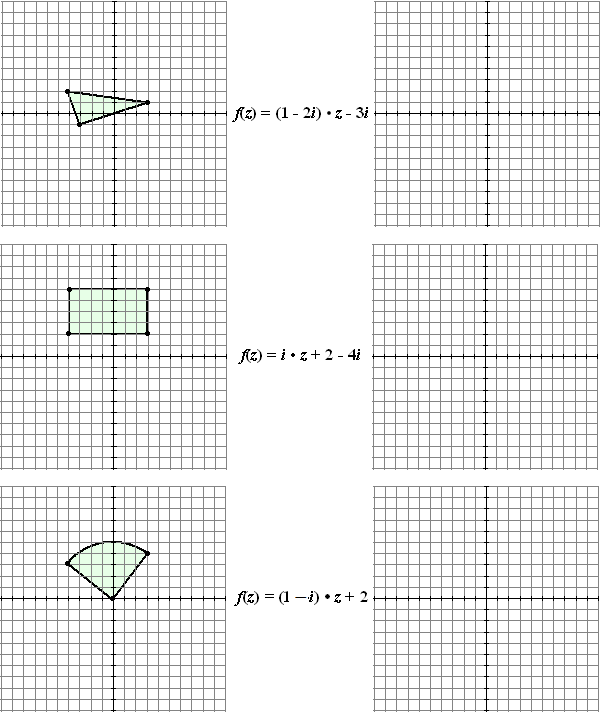
1.	Hieronder staan links drie figuren. Teken in de figuur rechts het beeld van deze figuren bij de functie die tussen de roosters staat.



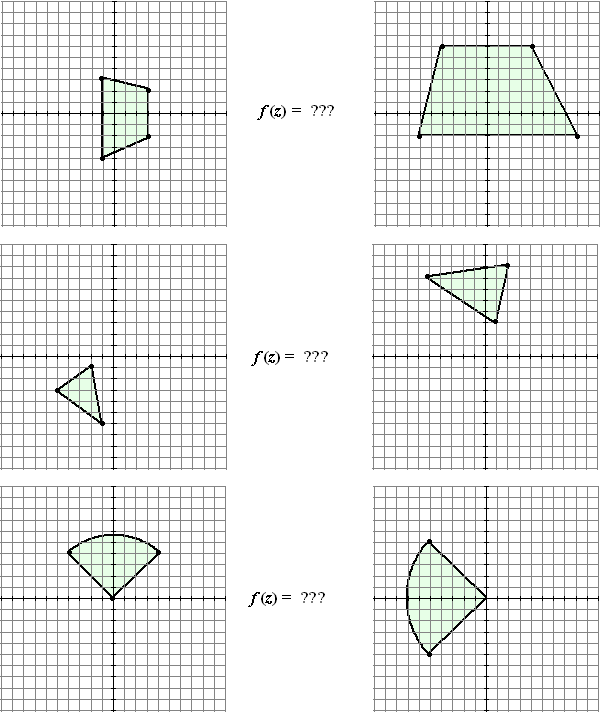
2.	Hieronder staan drie gebieden met hun beeld bij een lineaire functie van de vorm f(z) = (a + bi) • z Welke functie? (ofwel: wat zijn a en b?)



3.	De rechte lijn die in het reële vlak de lijn y = ax is, kun je in het complexe vlak voorstellen door de getallen z = x + iax

	a.	Leg uit waarom dat zo is.

	Als je op zo'n lijn de functie f(z) = (p + iq) • z toepast dan krijg je een beeldlijn met hellinggetal ^{(pa + q)}/_{(p - aq)}

	b.	Toon algebraïsch aan dat dat zo is.

	c.	Stel dat je door f(z) = (p + iq) • z de lijn y = 2x wilt laten overgaan in de lijn y = 5x Dan kan dat, als je het getal p + iq maar kiest op de lijn y = ³/₁₁x Toon aan dat dat zo is.

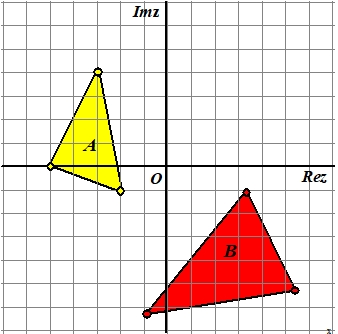
4.	Door een lineaire complexe functie wordt driehoek A in de figuur hiernaast afgebeeld op driehoek B. Geef het functievoorschrift.

Dekpunten.

We hebben nou al een boel tekeningetjes van gebieden z gehad met hun bijbehorende gebieden f(z). Die tekenden we steeds naast elkaar.
Maar stel dat je ze zoals de paarden hiernaast over elkaar heen legt? Dan zijn er vaak snijpunten van de figuur met zijn beeldfiguur. Sommige van die punten zijn misschien punten die door de functie op zichzelf worden afgebeeld.

Zulke snijpunten heten dekpunten en daarvoor geldt dus:

dekpunt: f(z) = z

Let dus goed op: een dekpunt is altijd een snijpunt van de figuur met zijn beeldfiguur, maar niet elk snijpunt is een dekpunt!

Neem bijvoorbeeld de eenvoudige functie f(z) = (cos¹/₄π + i • sin¹/₄π) • z.
Dat is niets anders dan een draaiing over 45º, dus een cirkel met middelpunt O wordt daardoor op zichzelf afgebeeld, maar toch zijn er op die cirkel geen dekpunten.

Voorbeeld.
Welke dekpunten heeft de functie f(z) = (2 + i) • z + 1 - 2i ?
Voor een dekpunt geldt f(z) = z dus moet gelden (2 + i) • z + 1 - 2i = z
⇒ (1 + i) • z = 2i - 1
⇒ z = ^{(2i - 1)}/_{(1
+ i)} = ¹/₂ + 1¹/₂i

5.	Gegeven is de complexe functie f(z) = (-1 + 4i) • z + 1 + 2i

	a.	Teken het beeld van het vierkant met hoekpunten -3 + 4i, 5 + 10i, 3 - 4i en 11 + 2i.

	b.	Bereken welk punt dekpunt van f is.

	c.	Leg uit hoe je dat punt uit de tekening van a) kunt herkennen.

	d.	Los op f(z) = f(¹/_z).

6.	Hieronder staat het vlakdeel V getekend waar de punten liggen waarvoor geldt r ≤ 4√2 en ⁵/₄π ≤ φ ≤ ⁷/₄π. Het is een kwart cirkel. Verder is gegeven de complexe functie f(z) = (1 + i) • z - 3 + 2i



	a.	Bereken de nulpunten van f(z).

	b.	Geef de coördinaten van de dekpunten van f(z).

	c.	Teken het beeld van de kwartcirkel hierboven onder de functie f(z).

	d.	Leg uit hoe je het dekpunt van f(z) uit de tekening van vraag c) kunt vinden zonder de coördinaten ervan te berekenen.

7.	Hiernaast staat het gebied G in het complexe vlak getekend waarvoor geldt: \| z \| < 2 en 0 < arg(z) < 30° Bekijk de complexe functie: f(z) = (1 + i) × z + 1 – 3i

	a.	Bereken het dekpunt van deze functie

	b.	Teken het beeld van gebied G bij deze functie

	c.	Schets het beeld van G bij de functie f(z) = z²


wortels			machtsfuncties