|
|
 |
|
Complexe wortels. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
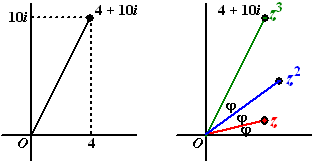
| Stel dat we willen oplossen de vergelijking
z3 = 4 +
10i |
Dan kun je proberen te schrijven
z = a + bi en dan (a + bi)3
gaan uitschrijven en dan het reële deel daarvan gelijk te stellen aan 4
en het imaginaire deel aan 10. Die vergelijkingen met a en b
los je dan op om a en b te vinden.
Tuurlijk, dat kun je best. Als je een regenachtige zondagmiddag niets te
doen hebt is het misschien nog wel leuk werk ook...Alhoewel ik bang ben
dat je die twee vergelijkingen niet kunt oplossen.......
Maar met de formule van de Moivre kan het stukken sneller.
Laten we beide kanten van de vergelijking met poolcoördinaten gaan
schrijven. |
• 4 + 10i =
√116 • (cos 1,19 + i • sin1,19)
(de 1,19 is uiteraard afgerond)
• Stel z = r(cosφ + i
• sinφ)
dan is z3
= r3 • (cos3φ + i •
sin3φ)
Dus moet gelden:
√116 • (cos 1,19 + i • sin1,19)
= r3
• (cos3φ + i • sin3φ)
Daaruit volgt r3 = √116
dus r = 2,21 en 3φ =
1,19 dus
φ = 0,40
Conclusie: z = 2,21 • (cos0,40 + i • sin0,40)
Of in andere vorm: z = 2,04 + 0,85i
Nog even controleren met het plaatje hiernaast: JA KLOPT! |
 |
|
|
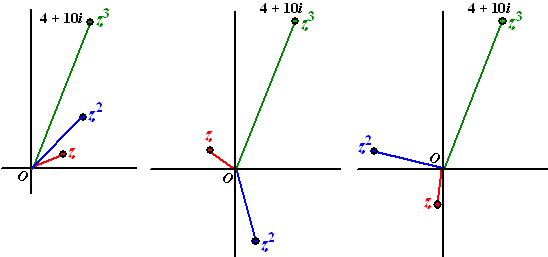
En toch klopt er iets niet!
Kijk maar naar de plaatjes hieronder. Daar staan nóg twee getallen z
waarvoor óók geldt z3 = 4 + 10i |
|
|
|
 |
|
|
Ga zelf maar na dat de hoeken en de lengtes
kloppen. Er is dus niet één oplossing voor deze vergelijking, maar er
zijn er drie, die je hiernaast ziet. Ze lijken zelfs netjes de
hoekpunten van een gelijkzijdige driehoek te zijn....
Hoe kan dat?
Wat hebben we gemist en hoe kunnen we dat oplossen?
De fout zit hem in de allereerste stap!
Daar stelden we dat 10 + 4i = √116 •
(cos 1,19 + i • sin1,19)
Dus r = √116 en
φ = 1,19.........
Dat klopt natuurlijk wel, maar het is niet volledig.
Immers, als je 2π optelt bij de hoek, dan kom
je ook in het zelfde punt uit! En ook bij 4π
en 6π en .....
Er had moeten staan
r =
√116 en
φ
= 1,19 + k • 2π |
 |
|
|
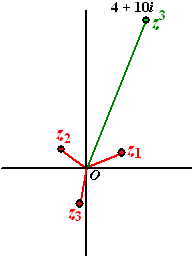
De rest van de oplossing was dan
zó gegaan: r = 2,21 en 3φ
= 1,19 + k • 2π dus
φ = 0,40 + k • 2/3π
Dat laatste had inderdaad tussen 0 en 2π DRIE
verschillende oplossingen gegeven, zoals we grafisch al zagen.
Die drie oplossingen hebben dezelfde r, en hun hoeken schelen
precies 2/3π
van elkaar, dus ze liggen inderdaad precies op de hoekpunten van een
gelijkzijdige driehoek.Hoe is het bij andere machten?
Verander de 3 in een n, dan komt er uiteindelijk te staan
φ = .... + k • 2/nπ
en op r heeft het geen invloed.
We vinden dus n oplossingen met dezelfde r die een
hoek 2/nπ
van elkaar verschillen.
De oplossingen liggen op de hoekpunten van een regelmatige n-hoek.
Tijd voor een conclusie: |
| |
|
|
zn =
a heeft n oplossingen.
die oplossingen liggen op de hoekpunten van
een regelmatige
n -hoek. |
|
|
|
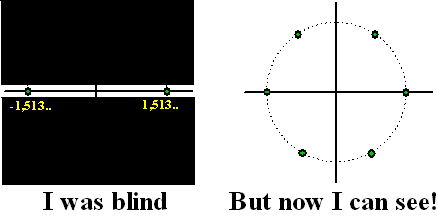
Kun je nagaan wat we vroeger
eigenlijk armoedig bezig waren.
Toen zeiden we bijvoorbeeld x6 = 12 dan
volgt daaruit x = (12)1/6 = 1,513...
En toen moesten we, omdat we graag wilden dat x6 een
functie was, er nog extra bijleren dat x = -121/6
óók een oplossing was. Terwijl er eigenlijk al die tijd nóg vier
oplossingen waren!!!
Maar ja, die zagen we niet omdat we zo'n beperkte bril ophadden, waarmee
we alleen de reële as in beeld hadden: |
|
|
|
 |
|
|
WAAUW! Een hele wereld lag voor
ons verborgen!
En nu we al die oplossingen zien, stappen we ook maar af van dat
krampachtige idee dat een wortel maar één uitkomst mag hebben. We moeten
eigenlijk wel. Eén speciaal geval bekijken gaat nog, maar zoveel extra
gevallen wordt een beetje te ingewikkeld.
Daarom zeggen we voortaan gewoon dat 3√x
drie uitkomsten heeft en 4√x
vier uitkomsten en 5√x vijf
uitkomsten enz. |
| |
|
|
Complexe wortels zijn meerwaardig |
|
| |
|
|
Trap er niet in! |
| |
|
Voor complexe wortels geldt NIET
meer de eigenschap √a •
√b = √(ab)
Als je daaraan blijft vasthouden krijg je rare dingen als dit:
√(-1) • √(-1) =
i • i = -1
√(-1) • √(-1) =
√(-1 • -1) = √(1)
= 1
Dus hebben we bewezen dat -1 = 1
Wat had je moeten zeggen?
√a heeft twee mogelijkheden, √b
heeft twee mogelijkheden, dus √(ab)
heeft 4 mogelijkheden (maximaal; er kunnen dubbelen verschijnen
natuurlijk).
In dit geval: √-1 = i of
-i
Dus √-1 • √-1
= i • i of i • -i of
-i • i of -i • -i en dat
is -1 of 1 of 1 of -1 |
| |
|
| |
|
|
 |
|
|
 |
|
vectoren |
|
|
lineaire functies |
|
|
|
| 1. |
Los op en geef in de vorm a + bi:
(bereken indien nodig a en b in twee decimalen). |
| |
|
|
|
|
|
|
| |
a. |
z3 = 8i |
|
e. |
z3 = 6 + 4i |
|
1.89 + 0.38i
-1.27 + 1.45i
-0,62 - 1.83i |
|
| |
b. |
z2 = 2 + 6i |
|
f. |
(z - i)3 = 3i
+ 5 |
|
1.77 + 1.32i
-1.16 + 2.37i
-0,61 - 2.69i |
|
| |
c. |
z5 = -32 |
|
1,62
± 1,18i
-0,62± 1,90i
-2 |
|
g. |
(2i + 3 + 2z)3 = 2
- 2i |
|
-0.82 - 1.18i
-1.69 - 0.32i
-2 - 1.5i |
|
| |
d. |
z4 = 1 + i |
|
±(1,07 + 0,21i)
±(0,21 - 1,07i)
|
|
h. |
(iz)5 = 2i |
|
1,15
0.35
± 1.09i
-0,93 ± 0.68i |
|
| |
|
|
|
|
|
|
| 2. |
Bereken alle mogelijke uitkomsten
van de volgende uitdrukkingen, en schrijf die in de vorm a
+ bi: |
| |
|
|
|
|
|
|
| |
a. |
√(2 - 3i) |
|
c. |
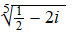 |
|
1.12 - 0.30i
0.63 + 0.97i
-0.72 + 0.90i
-1.08 - 0.41i
0.06 - 1.15i |
|
| |
b. |
√(2 + 2i) +
√(3i) |
|
±(2.78 + 1.87i)
±(0.33 - 0.58i)
|
|
d. |
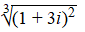 |
|
2.11 - 0.46i
-0.66 + 2.05i
-1.45 - 1.59i |
|
| |
|
|
|
|
|
|
 3. 3. |
Los op: (z2
+ 2i)3 = 4 + 5i |
|
±(1.43 - 0.51i)
en ±(0.31 - 1.21i) en
±(1.31 + 1.46i) |
|
| |
|
|
|
|
|
|
| 4. |
Een wortel exact....
In deze opgave ga je √(1/2√3
+ 1/2i)
berekenen. Dat ga je doen op twee verschillende manieren. |
| |
|
|
|
|
|
|
| |
a. |
Toon met de regel van de Moivre aan
dat geldt :
√(1/2√3
+ 1/2i)
= cos(1/12π)
+ i • sin(1/12π) |
| |
|
|
|
|
|
|
| |
Door te stellen
√(1/2√3
+ 1/2i)
= a + bi, dus (a + bi)2
= 1/2√3
+ 1/2i
kun je door de haakjes weg te werken twee vergelijkingen
opstellen voor a en b |
| |
|
|
|
|
|
|
| |
b. |
Toon aan dat geldt a2
- b2 = 1/2√3
en 2ab = 1/2 |
| |
|
|
| |
c. |
Toon aan dat daaruit volgt
a2 = 1/4√3
+ 1/2 |
| |
|
|
| |
d. |
Wat volgt daaruit voor de exacte
waarde van cos 1/12π? |
| |
|
| 5. |
Hiernaast zie je in het
complexe vlak een punt z getekend en daarmee ook
z2, z3, z4,
enz.
Er is ook een cirkel met straal 2 en middelpunt O getekend, maar
verder is er geen schaalverdeling. |
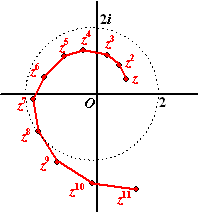 |
| |
|
|
|
|
| |
a. |
Hoe kun je in één
oogopslag zien dat de afstand van z tot O groter
dan 1 is? |
| |
|
|
|
|
| |
De machten van z
vormen een soort van spiraal. Het lijkt erop dat z8
bijna op de cirkel met straal 2 ligt, en dat z10
bijna op de negatieve imaginaire as ligt. |
| |
|
|
|
|
| |
b. |
Wat moet je voor z kiezen
zodat dat niet bijna klopt, maar exact? |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|