|
|||||
| 1. | |||||
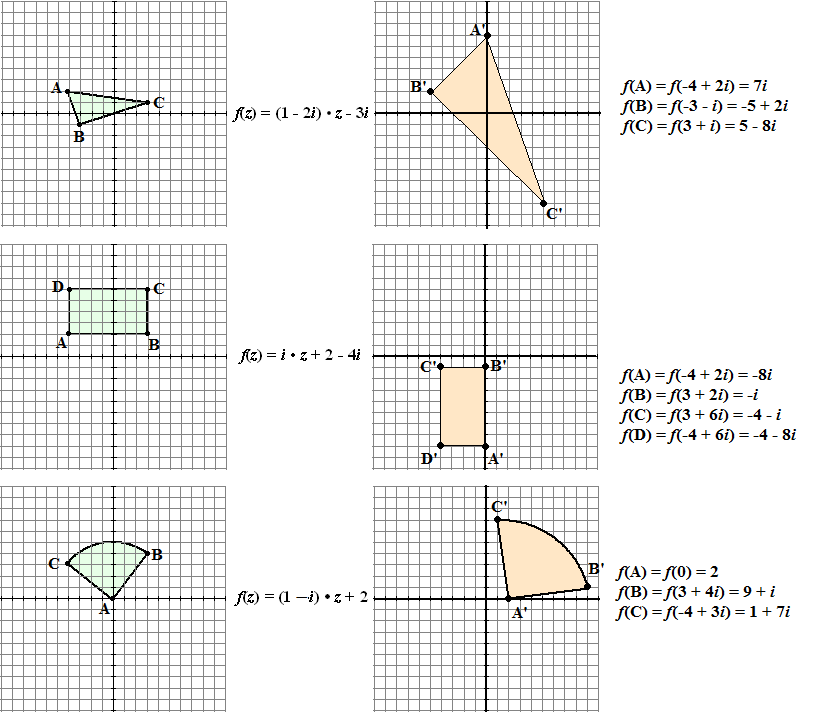 |
|||||
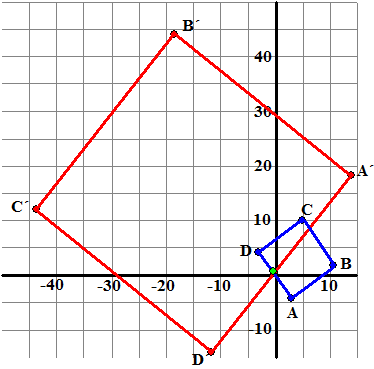
| 2. | a. | Zo te zien worden
alle lijnstukken twee keer zo lang, en wordt er over 90º gedraaid. Dat zou betekenen een vermenigvuldiging met 2i Het hoekpunt 3 + 2i zou dan terechtkomen op -4 + 6i en dat klopt precies, dus is er geen verschuiving meer nodig Kortom: f(z) = 2iz |
|||
| b | De oorspronkelijke
zijden zijn √25,
√26 en √13 en de zijden van het beeld zijn
√50, √52
en √26 dus dat is
√2 keer zo lang. -5 - 3i komt bijv. terecht op 2 + 8i dus (-5 - 3i)(a + bi) = (-5a + 3b) + i(-3a - 5b) Dus -5a + 3b = 2 en -3a - 5b = 8 -15a + 9b = 6 en 15a + 25b = -40 optellen: 34b = -34 dus b = -1 en dan is a = -1 (-1 - i heeft inderdaad lengte √2) Kortom f(z) = (-1 - i)z |
||||
| c. | De lijnstukken worden 1,25 keer
zo lang, en er wordt gedraaid over 90º Dat betekent vermenigvuldiging met 1,25i Kortom: f(z) = 1,25iz |
||||
| 3. | a. | Het punt (x,
y) in het reële vlak komt overeen met (Rez, Imz)
in het complexe vlak. Dus y = ax betekent Imz = a • Rez Dus als Rez = x dan is Imz = ax en dan is z het punt x + iax |
|||
| b. | (p + iq) • (x
+ iax) = px + iqx + ipax - qax = (p - qa)x + ix(q + pa) In het reële vlak is dat het punt ((p - qa)x , x(q + pa)) Voor zo'n punt P geldt: helling OP is y/x = x(q + pa)/x(p - qa) = (q + pa)/(p - qa) |
||||
| c. | Je begint met y
= 2x dus a = 2 Je eindigt met y = 5x dus (q + pa)/(p - qa)= 5 Daaruit volgt q + pa = 5(p - qa) dus q + 2p = 5(p - 2q) q + 2p = 5p - 10q 3p = 11q q = 3/11p Het complexe getal (p + iq) heeft dan in het reële vlak coördinaten waarvoor y = 3/11x |
||||
| 5. | a. | f(-3 + 4i)
= (-1 + 4i) • (-3 + 4i) + 1 + 2i
= 3 - 4i - 12i - 16 + 1 + 2i =
-12 - 14i f( 5 + 10i) = (-1 + 4i) • ( 5 + 10i) + 1 + 2i = -5 - 10i + 20i - 40 + 1 + 2i = -44 + 12i f(3 - 4i) = (-1 + 4i) • ( 3 - 4i) + 1 + 2i = -3 + 4i + 12i + 16 + 1 + 2i = 14 + 18i f(11 + 2i) = (-1 + 4i) • (11 + 2i) + 1 + 2i = -11 - 2i + 44i - 8 + 1 + 2i = -18 + 44i |
|||
|
|
|||||
| b. | z = (-1 + 4i)
• z + 1 + 2i z - (-1 + 4i)z = 1 + 2i z(2 - 4i) = 1 + 2i z = (1 + 2i)/(2 - 4i) z = (1 + 2i)/ (2 - 4i) • (2 + 4i)/(2 + 4i) = (2 + 4i + 4i - 8)/(4 + 16) = (-6 + 8i)/20 = -0,3 + 0,4i : het groene punt uit de tekening |
||||
| c. | Het is het punt dat in beide vierkanten op dezelfde plaats ten opzichte van de hoekpunten ligt. | ||||
| d. | (-1 + 4i) • z + 1 + 2i
=
(-1 + 4i) • 1/z + 1 + 2i
(-1 + 4i) • z2 + (1 + 2i) • z = (-1 + 4i) + (1 + 2i) • z (-1 + 4i) • z2 = (-1 + 4i) z2 = 1 z = 1 ∨ z = -1 |
||||
| 6. | a. |
(1 +
i) • z - 3 + 2i = 0 (1 + i) • z = 3 - 2i z = (3 - 2i)/(1 + i) z = (3 - 2i)/(1 + i) • (1 - i)/(1 - i) = (3 - 3i - 2i - 2)/(1 + 1) = (1 - 5i)/2 = 0,5 - 2,5i |
|||
| b. | z =
(1 +
i) • z - 3 + 2i z - (1 + i)z = -3 + 2i -iz = -3 + 2i z = (-3 + 2i)/-i = 3/i - 2 = -2 - 3i |
||||
| c. |
(1 +
i) • z betekent vermenigvuldigen met factor
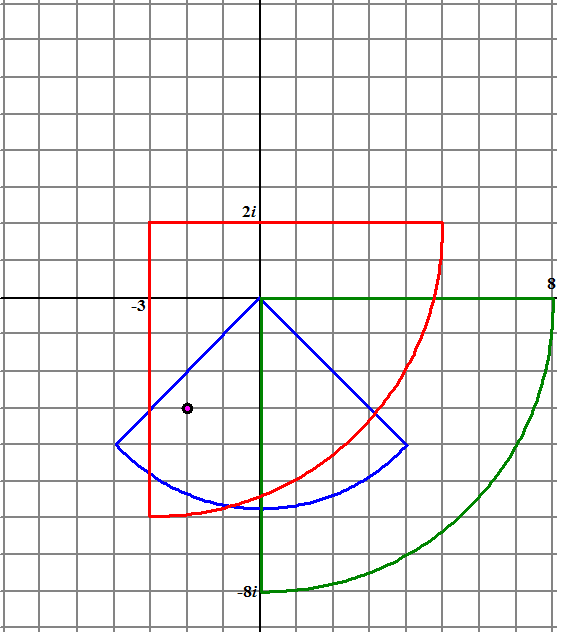
√2 en draaien over 45º -3 + 2i is daarna een translatie Dat geeft het volgende beeld: |
||||
|
|
|||||
| Het groene deel is na vermenigvuldiging met 1 + i , het rode is daarna na translatie -3 + 2i | |||||
| d. | Het is het paarse punt. Dat is het punt dat in beide cirkeldelen op "dezelfde plaats" ligt. | ||||
| 7. | a. |
(1 + i)
×
z + 1 – 3i = z z(1 + i - 1) = 3i - 1 z • i = 3i - 1 z = 3 - 1/i = 3 + i |
|||
| b. |
(1 + i)
×
z betekent draaien over 45º en vermenigvuldigen met
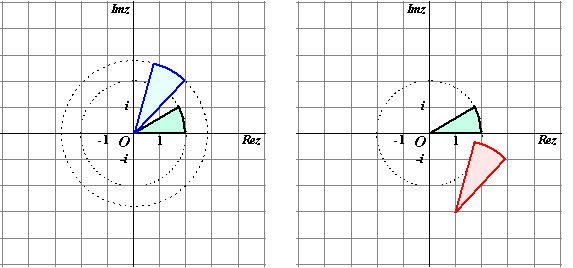
factor √2 (geeft het blauwe gebied hieronder) + 1 – 3i is daarna een translatie (geeft het rode gebied hieronder) |
||||
|
|
|||||
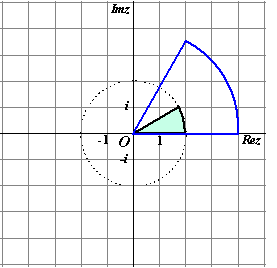
| c. | De hoek van elk getal
wordt dubbel zo groot, dus dat geeft hoeken tussen 0º en 60º De afstand tot de oorsprong wordt gekwadrateerd dus dat geeft afstanden tussen 0 en 22 = 4 Samen geeft dat het blauwe gebied hieronder |
||||
|
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||