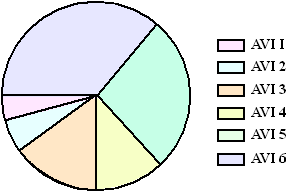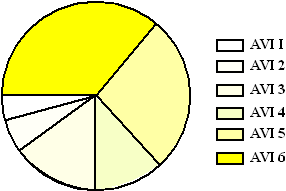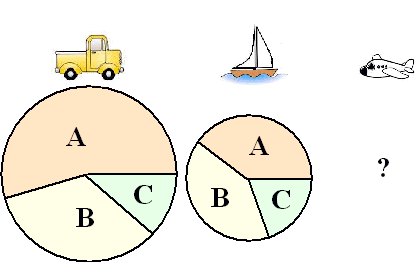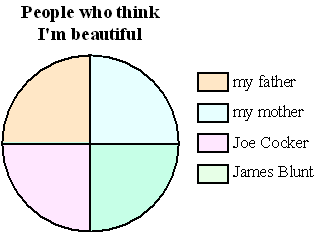
cirkeldiagram


Cirkeldiagram.	© h.hofstede (h.hofstede@hogeland.nl)

Een cirkeldiagram heet ook wel een taartdiagram (Engels: "Pie Chart") of een schijfdiagram. Het wordt vooral veel gebruikt om aan te geven hoe iets is onderverdeeld in verschillende subcategorieën. Dat kan natuurlijk ook wel met een staafdiagram, maar vooral als de groottes van de onderdelen nogal sterk van elkaar verschillen is een cirkeldiagram vaak duidelijker. Bovendien geeft een cirkeldiagram in één oogopslag aan hoeveelste deel van het geheel een bepaalde subcategorie is.

Hiernaast zie je bijvoorbeeld een cirkeldiagram waarin staat welk leesniveau (AVI-1 tm AVI-6) de kinderen van groep 4 van een basisschool hebben gehaald. Je ziet bijv. in één oogopslag dat driekwart van hen minstens niveau 4 heeft gehaald.

En hieronder een wel erg originele "Pie chart":

De berekeningen.

Die zijn gelukkig erg erg makkelijk. Als je je maar bedenkt dat de oppervlakte van een cirkelsegment bepaald wordt door de hoek in het midden. En omdat de hele cirkel 360º is, hoort daarbij dus 100%.

Bij 360º hoort 100%

Wil je andere groottes berekenen dan gebruik je bijvoorbeeld een verhoudingsschema of welke andere manier dan ook waarmee je normaal gesproken verhoudingen berekent..

voorbeeld 1.
In het cirkeldiagram hierboven hoort bij leesniveau AVI-6 (het donkerpaarse deel) een middelpuntshoek van 129º.
Het percentage van dit deel zal daarom gelijk zijn aan ¹²⁹/₃₆₀ • 100% = 35,8%

voorbeeld 2.
Stel dat je in een cirkeldiagram een deel wilt tekenen dat 85% van het totaal is.
Dan zal de bijbehorende middelpuntshoek gelijk zijn aan ⁸⁵/₁₀₀ • 360 = 306º

Oplichterij/Manipulatie.

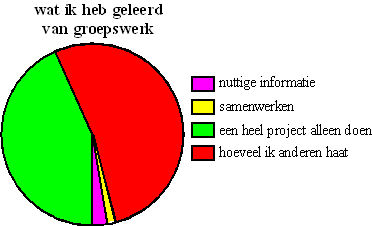
Als je graag op een bepaalde sector van je cirkeldiagram de nadruk wilt leggen, dan kun je dat bijvoorbeeld doen door die sector een fellere kleur dan de anderen te geven.
Hiernaast is het bovenstaande diagram nogmaals getekend, maar nu door iemand die er de nadruk op wil leggen dat toch wel een erg groot deel van de kinderen al de hogere niveaus hebben gehaald.

Er is nog een subtielere manier om dat te doen, en dat is door gebruik te maken van perspectief. Wat dichter bij je is ziet er nou eenmaal groter uit.

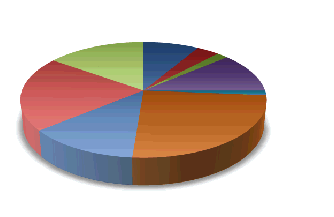
Een voorbeeld zie je hiernaast. De oranje en de lichtblauwe en rode sectoren zijn al behoorlijk groot, maar de tekenaar wil dat kennelijk graag nog eens extra benadrukken door ze naar ons toe te keren en ze dus vooraan te tekenen.
Om het helemaal af te maken zou hij ze dus eigenlijk ook nog een feller kleurtje dan de andere sectoren moeten geven.

Hiernaast zie je hoe je nog eens extra de aandacht kunt vestigen op een deel van het cirkeldiagram door dat er als een echte taartpunt uit te laten steken.

Het rode deel is al het grootst, zit al aan de voorkant, is het felst gekleurd, en steekt er ook nog eens extra uit! Als je er nú niet van overtuigd bent dat een website de beste marketingmanier is, dan weet ik het ook niet meer!!!

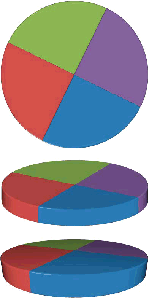
Hiernaast zie je dat nog eens overduidelijk. Het bovenste cirkeldiagram staat eronder nogmaals twee keer getekend, maar dan onder verschillende hoeken.

Je ziet dat die twee onderaan er heel verschillend uitzien alhoewel het echt twee keer precies hetzelfde cirkeldiagram is!

De tekening komt uit het prachtige artikel "Save the Pies for Dessert" van Stephen Few, dat gaat over de nadelen van cirkeldiagrammen vergeleken met histogrammen en lijndiagrammen, en dat je kunt vinden op

http://www.perceptualedge.com/articles/08-21-07.pdf

Andere varianten.

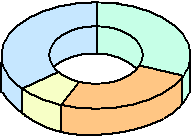
1. Ringdiagram.

Spreekt voor zich, denk ik. 't Is gewoon een cirkeldiagram met het midden daaruit weggelaten. Voor het mooi. Zou bijvoorbeeld aardig zijn om de hoeveelheid donuts die Amerikaanse agenten per dagdeel eten weer te geven....

Bijkomend voordeel is dan natuurlijk dat je dat binnenste deel kunt vullen met een nieuw ander cirkeldiagram.

Dat is hiernaast gebeurd (het middelste deel is ietsje verhoogd getekend). Daarbij moet je er wel om denken dat de verhoudingen tussen binnenste en buitenste cirkeldiagram blijven kloppen!

Als de straal van het middelste diagram bijvoorbeeld de helft is van het buitenste, dan is de oppervlakte maar een kwart!!!

2. Cirkeldiagram met onderverdeling.

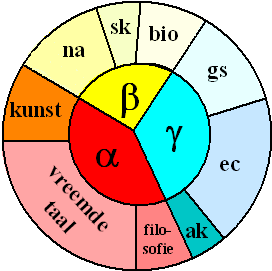
Een beetje voortbordurend op het vorige ringdiagram kun je dit natuurlijk wel handig gebruiken om een cirkeldiagram met een onderverdeling erin te maken.

Hiernaast zie je de pakketkeuze van een aantal middelbare school leerlingen, gesplitst naar alpha- béta- en gammavakken.

Alleen de keuzevakken zijn gegeven, verplichte vakken als Nederlands, Engels en Wiskunde zijn niet meegerekend.

Je ziet dat je uit dit cirkeldiagram in één keer een beeld hebt over de verdeling α-β-γ maar ook nog de keuze van de afzonderlijke vakken kunt vinden. Handig!!!

3. Cirkeldiagram in cirkeldiagram.

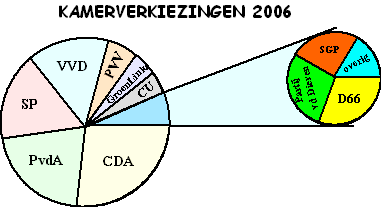
Als er erg veel kleine gebiedjes in een cirkeldiagram zijn, is het soms overzichtelijker om die samen één gebied te geven en dat dan weer uit te splitsen in een nieuw cirkeldiagram.

Hiernaast zie je dat voor de stemmenverdeling bij de kamerverkiezingen van 2006.

Die vier kleine partijen hebben elk minder dan 2% van de stemmen, dus dat zou je in het grote cirkeldiagram amper zien.

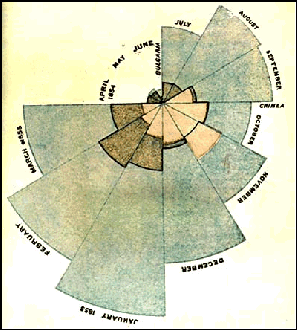
4. Pooldiagram.

Hiernaast zie je een beroemd diagram. Het is de zogenaamde "coxcomb" gepubliceerd door Florence Nightingale. Voor de maanden juli 1854 tot en met maart 1855 geeft het het aantal doden weer tijdens de Krimoorlog ten gevolge van verschillende oorzaken.

De binnenste oranjeachtige gebieden zijn de doden ten gevolgen van oorlogswonden. De groenige buitenste gebieden zijn de doden ten gevolge van besmettelijke ziektes die voorkomen kunnen worden door betere hygiëne, zoals cholera en typhus. De bruinige gebieden zijn de doden met "overige" oorzaken. Het diagram is zó gemaakt dat elke maand eenzelfde middelpuntshoek heeft, en dat de oppervlakten in verhouding tot de aantallen doden staan.

Het zal duidelijk zijn dat Florence Nightingale met dit diagram wilde pleiten voor betere hygiëne in de militaire hospitalen.

Je eigen draagbare cirkeldiagram!

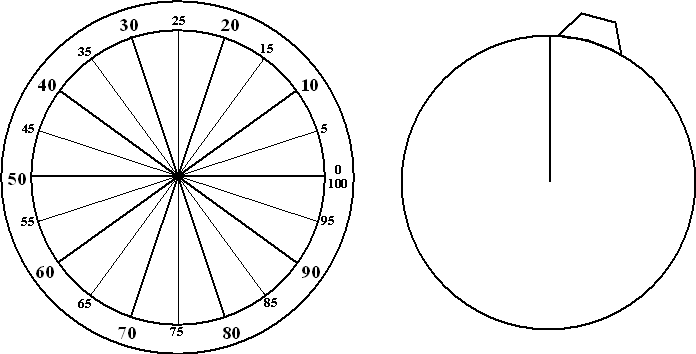
Natuurlijk wil ook jij na deze les overal ter plekke instantaan een cirkeldiagram kunnen maken. En dat kan met onderstaande bouwplaat!!!
Knip de linkerfiguur uit op stevig karton.
Knip vervolgens van de rechterfiguur meerdere exemplaren uit, elk op een ander gekleurd soort papier. De lijn van midden boven naar het middelpunt toe moet je inknippen.

Als je nu jouw gekleurde exemplaren op de kartonnen schijf legt en daarna over het midden een klein kartonnen cirkeltje met een splitpen vastmaakt, dan kun je door de gekleurde cirkels te draaien een willekeurig cirkeldiagram zomaar tevoorschijn toveren. De getallen aan de rand van de onderste kartonnen schijf geven de procenten aan.
COOL toch?.....

Maak van de volgende tabel een cirkeldiagram.
Hier staan de aantallen (percentages) honden, katten, vissen, vogels en overige dieren die dierenwinkel "ZooPlus" het afgelopen jaar heeft verkocht.

soort	hond	kat	vogel	vis	overig
aantal	24%	40%	12%	18%	6%

Het cirkeldiagram hiernaast geeft aan hoe een middelbare scholier zijn doordeweekse dag doorbrengt.
Maak van dit cirkeldiagram een staafdiagram. Zet op de verticale as de relatieve frequentie in procenten.

Hiernaast zie je de resultaten van een enquête over groepswerk.

Hoeveel procent van de deelnemers doet naar zijn eigen idee een groepsproject toch eigenlijk alleen?

Cirkeldiagrammen met elkaar vergelijken

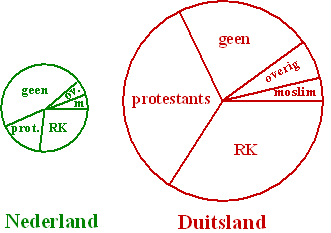
Het kan zijn dat je in één figuur graag meerdere cirkeldiagrammen wilt maken. Als elk cirkeldiagram een bepaalde "groep" voorstelt, dan wil je natuurlijk wél dat de oppervlakten van die dagrammen ook overeenkomen met de grootte van die "groepen".

Neem bijvoorbeeld de twee cirkeldiagrammen hiernaast. Daarin staat de verdeling van de verschillende religies in 2005 voor de landen Nederland en Duitsland.
Maar omdat Duitsland veel meer inwoners (82 miljoen) heeft dan Nederland (16 miljoen) is dat diagram natuurlijk veel groter getekend.

De vraag is natuurlijk: Hoeveel groter?

Nou kijk, dat zit zó: je wilt natuurlijk dat de oppervlakten van de cirkels een maat zijn voor het aantal inwoners. De oppervlakte van een cirkel is gelijk aan pr² , dus die hangt af van r². Daarom moeten de r² van de cirkel van Duitsland en die van Nederland dezelfde verhouding hebben als hun aantallen inwoners.
Stel bijvoorbeeld dat de straal van de Nederland-cirkel gelijk is aan 3 cm.
Dan kun je de straal van de Duitsland-cirkel met een verhoudingstabel berekenen, als je daar maar de r² in zet, en niet de r zélf. Dus zó:

	Nederland	Duitsland
r²	9	?
inwoners	16 miljoen	82 miljoen

Daaruit volgt dat de r² voor Duitsland gelijk is aan ^{9 • 82}/₁₆ = 46,125, dus de straal is √46,125 ≈ 6,8 cm.
Conclusie:

Maak een verhoudingstabel tussen de aantallen en r²


statplot TI-83			steel- en bladdiagram

Het verzendbedrijf Parcel International (PI) vervoert pakjes.
Dat doet men op drie manieren: over land, over water en door de lucht. In het cirkeldiagram hiernaast zie je hoeveel pakjes voor het jaar 2011 bij elk van deze drie categorieën horen.

Hoeveel procent van de pakjes werd door de lucht vervoerd?

12 á 13

PI verzond in 2011 in totaal 456124 pakjes over water .

Hoeveel pakjes werden over land vervoerd in 2011?

≈880000

Het vervoer over land gaat eigenlijk op twee verschillende manieren: binnen een stad meestal per fietskoerier, en tussen steden per vrachtwagen. In 2011 werd 38% van de pakjes over land per fietskoerier verzonden en 62% per vrachtwagen.

Geef deze twee gebieden aan in het cirkeldiagram hierboven.

Natuurlijk is het vervoeren van alle pakjes niet even duur. Men onderscheidt bij PI drie categorieën.
Categorie A: < 8€ en categorie B: €8 -< €20 en categorie C: €20 -< €50.
Hieronder zie je de bijbehorende cirkeldiagrammen

Maak een schatting voor de totale inkomsten voor PI in 2011 voor het vervoer over water.

≈€640000

Teken ook het derde cirkeldiagram, als je weet dat door de lucht alleen de categorieën B en C bestaan, waarbij 65% van de pakjes in categorie C valt en 35% in categorie B.

Hieronder zie je twee cirkeldiagrammen, die het aantal stemmers bij de laatste verkiezingen op de grootste partijen weergeven.

Het grootste diagram is nog niet volledig. Het is gebaseerd op de gegevens van de gemeente Roermond, die in onderstaande tabel staan.

Partij	CDA	VVD	PVV	PvdA	anders
Stemmers	8540	4500	6230	3590	1147

Maak het diagram van Roermond af. Leg duidelijk uit

In Roermond heeft 82% van de stemgerechtigden inderdaad gestemd. Van de hele bevolking van Roermond was 72% stemgerechtigd.

Hoeveel inwoners heeft Roermond?

Het kleinste diagram is van de gemeente Coevorden.
Hoeveel inwoners van Coevorden stemden op de PvdA?

Hieronder staan de gegevens van drie grote scholengemeenschappen voor VMBO, HAVO en VWO

	VMBO	HAVO	VWO
RSG de Hanze	240	80	50
Hoogland College	310	280	190
VS de Koepel	100	120	50

Zet deze gegevens uit in drie cirkeldiagrammen.

Er bestaan een heleboel soorten Russen.
Zo heb je Groot-Russen, Oekraïeners, Wit-Russen, Armeniërs, Georgiërs, Turkmenen, Oezbeken, Tadzjieken, Kazachen, Moldaviërs, Esten, Letten, Litouwers, Azerbaidzjanen, Kirgiezen en Georgiërs.
In de volgende cirkeldiagrammen staat van vier Russische republieken de samenstelling van de bevolking in 1976.

De republiek Azerbaidzjan had in 1976 in totaal 6,1 miljoen inwoners.

Hoeveel inwoners had Armenië in 1976?

Hoeveel Groot-Russen woonden er in Kazachstan in 1976?

In land A leven 3 miljoen mensen en daarvan werkt 35% in de landbouw.
In land B leven 1 miljoen mensen en daarvan werkt 75% in de landbouw.
Verwerk deze gegevens is twee cirkeldiagrammen.

In de volgende tabel staat voor een aantal straten hoeveel tijd een collectant eraan heeft besteed en ook hoeveel geld dat heeft opgeleverd.

straat	kerklaan	jachtlaan	lindestraat	hofplein	hyacintstraat
tijd (min)	40	75	25	120	100
opbrengst	€32,-	€50,-	€38,-	€60,-	€74,-

Maak hiervan een pooldiagram zodat de middelpuntshoek de tijd weergeeft en de oppervlakte de opbrengst.

Subtiele manieren om dingen duidelijk te maken: