boxplot


De Boxplot.	© h.hofstede (h.hofstede@hogeland.nl)

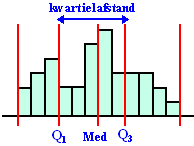
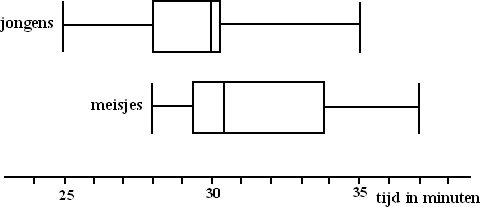
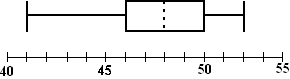
Bij het bekijken van de spreiding van een frequentieverdeling kwamen we de kwartielafstand tegen. Daarbij hoorde het plaatje hiernaast.
De gegevens werden verdeeld in 4 groepen met elk evenveel getallen (dus elk 25% van de getallen).
De kwartielen Q₁ en Q₃ waren de getallen op de x-as die bij 25% en bij 75% van de metingen lagen. De mediaan ligt bij 50% en die zou je dus het tweede kwartiel Q₂ kunnen noemen.

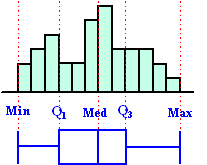
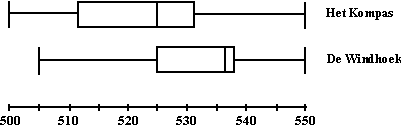
Als je het kleinste getal en het grootste getal nou óók meeneemt (als Q₀ en Q₄ bijvoorbeeld), dan kun je het plaatje onder het histogram hiernaast tekenen.

Zo'n plaatje heet een Boxplot.

Het geeft een redelijk beeld van de spreiding van een verdeling. Beter dan alleen de kwartielafstand, omdat nu toch ook de grootste en kleinste metingen zijn aangegeven.

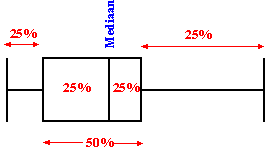
Bedenk goed dat in elk van de vier delen van de boxplot zich 25% van de metingen bevindt. Het "doosje" in het midden bevat dus de helft van alle metingen:

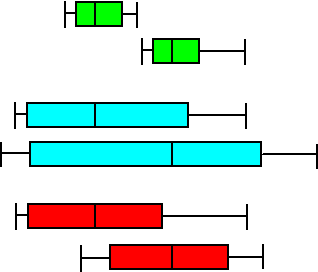
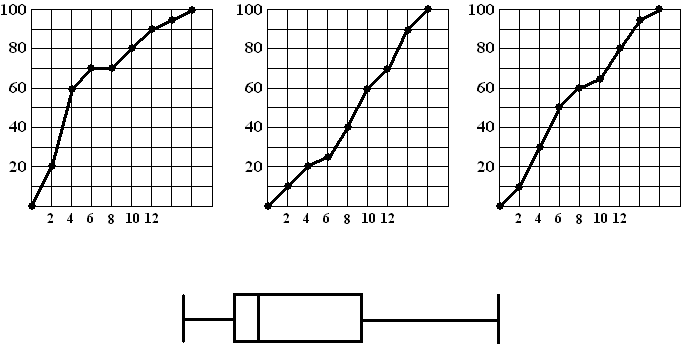
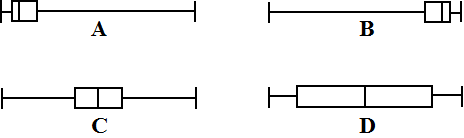
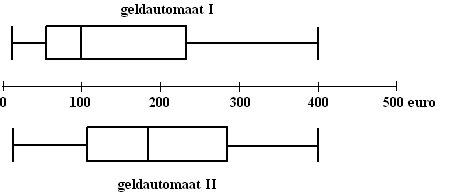
In het Engels heet deze figuur een "Box-and-Whisker plot"; ofwel letterlijk vertaald een "doosje met snorharen". En inderdaad is een oudere Nederlandse naam ook wel een "snorrendoos" of "doosdiagram".

OPMERKING voor gevorderden
In de meeste statistische softwarepakketten (zoals het beroemdste SPSS programma) worden boxplots nog iets anders getekend. De afstand tussen Q1 en Q3 wordt de kwartielafstand genoemd, en punten die nog verder dan 1,5 keer die kwartielafstand van Q3 (naar rechts) of van Q1 (naar links) af liggen worden beschouwd als meetfouten en niet meegerekend. Ze worden vaak apart naast de linker- of rechterkant van het boxplot aangegeven)

Het verschil tussen twee groepen.

Je kunt een boxplot handig gebruiken om iets duidelijker aan te geven of er tussen twee metingen van verschillende groepen een (groot) verschil zit of niet.
Hieronder zie je drie setjes (in drie kleuren) van twee boxplots. De medianen van de drie bovenstens zijn gelijk en ook de medianen van de drie ondersten.

Wat alleen de medianen betreft zou je dus kunnen stellen dat de verschillen tussen de bovenste en de onderste boxplots in alle drie de gevallen hetzelfde zijn.
Toch is dat duidelijk niet zo!
De groene twee verschillen eigenlijk heel veel: er zijn eigenlijk helemaal geen gelijke metingen geweest, alles is verschillend. De grootste van de ene is nog kleiner dan de kleinste van de tweede.
De blauwe twee verschillen erg weinig, de twee middelste blauwe boxen zijn aardig vergelijkbaar, er overlappen veel metingen.
De roden zitten daar een beetje tussen in. Niet heel veel verschillend zoals de groenen, ook niet erg weinig zoals de blauwen.

Maar ja, wat vinden we een "groot" verschil en wat een "klein". Kwestie van smaak?
Je snapt wel dat een "kwestie van smaak" niet kan in de wiskunde. We maken daarom (nog steeds vrij willekeurig) de volgende afspraak:
(daarbij bedoelen we met de "box" van een boxplot het deel tussen Q1 en Q3: het eigenlijke doosje)

Het verschil tussen twee boxplots:
de boxen overlappen helemaal niet.	het verschil is groot
de boxen overlappen wel, en minstens één van beide medianen ligt buiten de box van de andere plot.	het verschil is middelmatig
alle andere gevallen.	het verschil is klein

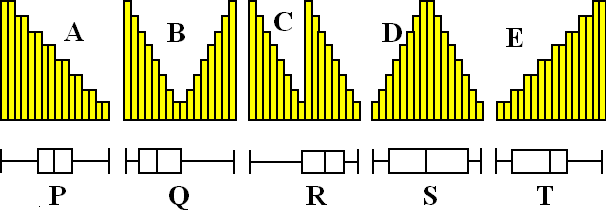
Boxplot en Histogram.

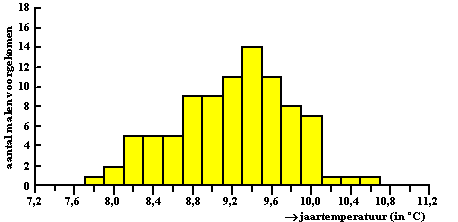
Er is (natuurlijk) een duidelijk verband tussen de vorm van een boxplot en de vorm van een histogram. Dat kun je het makkelijkst als volgt voorstellen.
Stel dat je een boekenplank hebt met 4 vakjes (de boxplot).

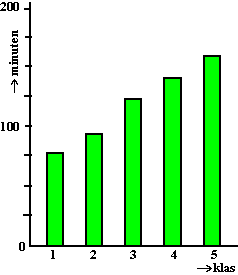
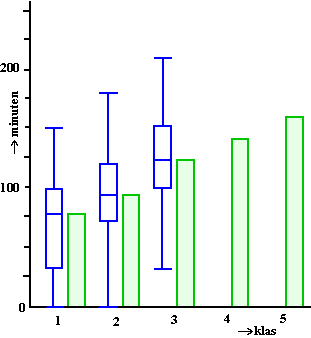
Stel verder dat je daar 100 boeken op moet leggen (je metingen), waarbij in elk vakje evenveel boeken moeten komen (dus elk 25). Als je die dan ongeveer in gelijke stapels legt, dan ziet dat er van voren ongeveer zó uit:

En daar zie je dan ongeveer een histogram.
Dus dit is logisch:


spreidingsbreedte, kwartielafstand			standaarddeviatie

Een aantal mensen is gevraagd hoeveel geld ze afgelopen jaarwisseling aan vuurwerk hebben uitgegeven. Dat leverde de volgende serie bedragen op:

14 25 28 16 50 128 87 92 54 50 40 32 60
65 75 82 20 54 50 34 45 78 90 90 15 20
45 48 72 81 32 34 10 10 15 46 156 145 65

Maak van deze bedragen een boxplot.

Hieronder staan vijf histogrammen (A tm E) met daaronder vijf boxplots (P tm S). Leg uit welk histogram bij welke boxplot hoort. Doe dat zonder bij elk histogram daadwerkelijk een boxplot te gaan tekenen.

Hieronder staan drie cumulatieve frequentiepolygonen en één boxplot

Onderzoek welk van de drie polygonen bij de boxplot hoort.

Schets ook bij de andere twee polygonen een boxplot.

Het staafdiagram hiernaast geeft het gemiddeld aantal minuten dat HAVO-scholieren per dag verspillen met computerspelletjes.
De gegevens zijn gebaseerd op de volgende tabel:

klas minuten:	1	2	3	4	5
0-30	4	3	-	-	-
30-60	15	6	1	-	-
60-90	30	18	5	2	1
90-120	20	20	12	8	3
120-150	8	12	12	12	6
150-180	-	4	8	10	14
180-210	-	-	2	6	8
210-240	-	-	-	-	2

De wiskundeleraar vindt het maar jammer dat alleen de gemiddelde tijden in het staafdiagram te vinden zijn. Het lijkt hem leuker en meer informatief als ook de spreiding te zien is. Daarom stelt hij voor om, in plaats van een staaf, een boxplot in het diagram te tekenen. Hiernaast is daarvan al een beginnetje gemaakt. De staven van het staafdiagram zijn overgenomen.

Maak ook de laatste twee boxplots

De middens van de boxplots vallen wel ongeveer maar niet precies samen met de hoogtes van de staven. Leg duidelijk uit hoe dat komt.

Carola computert nu ongeveer twee uur per dag. Als haar ouders daar wat van zeggen beweert ze dat een kwart van haar klas langer computert.
In welke klas kan zij zitten?

Als training voor de Coopertest houdt de gymleraar elk jaar een bosloop. Hieronder zie je twee boxplots waarin de tijden staan die leerlingen nodig hadden voor deze bosloop. Er is een aparte boxplot voor de meisjes en eentje voor de jongens.

In totaal liepen er 32 jongens en 28 meisjes mee, dus 60 leerlingen.

Op welke plaats eindigde het snelste meisje?

Rond welk tijdstip kwam er een grote groep tegelijk binnen?

Welke tijd liep degene die als 38^ste eindigde ongeveer?

Wat kun je zeggen over de plaats waarop de langzaamste jongen eindigde?

Hieronder zie je in één figuur de Citoscores van de twee basisscholen “Het Kompas” en “de Windhoek”
Op Het Kompas deden 36 leerlingen mee en op “De Windhoek deden 60 leerlingen mee.

Hoeveel procent van het totaal van alle leerlingen van deze twee scholen haalde een score van 525 of meer?

65,6%

Hoe groot is de spreidingsbreedte van “De Windhoek”?

Hoe groot is de kwartielafstand van “Het Kompas"?

»20

In de buurt van welke score scoorden waarschijnlijk de meeste leerlingen? Leg duidelijk uit!

537

examenvraagstuk HAVO wiskunde A, 1990.

De gemiddelde temperatuur over een kalenderjaar, de zogenaamde jaartemperatuur, gedraagt zich nogal grillig. Zo was de jaartemperatuur de afgelopen twee jaar uitzonderlijk hoog. In 1989 was de jaartemperatuur liefst 1,4 ºC hoger dan het gemiddelde van alle jaartemperaturen over deze eeuw (9,2ºC) tot nu toe.
In onderstaand histogram (met klassenbreedte 0,2ºC) staat de frequentieverdeling van de jaartemperatuur over het tijdvak 1900-1989 uitgezet.

Teken de box-plot bij deze frequentieverdeling.

examenvraagstuk HAVO wiskunde A, 1996.

Mensen verplaatsen zich van de ene naar de andere plaats, vanwege werk, boodschappen, enzovoort. In 1984 heeft het Centraal Bureau voor de Statistiek onderzoek gedaan naar die verplaatsingen. Daarbij werd zowel op de afstand als op de vervoerswijze gelet.
In de volgende tabel staan resultaten van dat onderzoek. Hierin zijn de afstanden in klassen ingedeeld. In de tabel is bijvoorbeeld te zien dat van de 97 verplaatsingen in de categorie 'autobestuurder' er 19 waren met een afstand tussen de 1 en 2,5 km.

Afstand	Autobestuurder	Openbaar vervoer	Fietsen	Lopen
0 - 0,5 km 0,5 - 1 km 1 - 2,5 km 2,5 - 3,7 km 3,7 - 5 km 5 - 7,5 km 7,5 - 10 km 10 - 15 km 15 - 20 km 20 km of meer	1 4 19 12 7 14 6 10 6 18	0 0 1 2 1 2 1 2 1 6	5 14 37 13 5 9 3 3 2 0	18 16 18 3 2 1 0 0 0 0
Totaal	97	16	91	58

Stel dat in de categorieën 'Fietsen' en 'Lopen' van deze tabel de waarnemingen binnen elke klasse gelijkmatig zijn verdeeld.

In de figuur hier onder zie je vier boxplots A, B, C en D.

Welke van deze vier boxplots past het best bij de categorie 'Lopen'? Licht je antwoord toe.

Leg uit waarom de mediaan van de categorie 'Lopen' in de klasse 0,5-1 km ligt.

examenvraagstuk HAVO wiskunde A, 2002.

Uit de wielersport komen de laatste jaren regelmatig berichten over dopinggebruik. Wielrenners lijken steeds vaker naar verboden middelen te grijpen om hun prestaties te verhogen. Een van de meest genoemde stoffen is erytropoëtine, kortweg EPO. Dit middel bevordert de aanmaak van rode bloedlichaampjes, waardoor de zuurstoftransportfunctie van het bloed wordt vergroot. Je gaat hierdoor beter presteren.
De hematocrietwaarde is de hoeveelheid rode bloedlichaampjes als percentage van de totale hoeveelheid bloed. Die hematocrietwaarde stijgt dus als een wielrenner EPO gaat gebruiken.

Bij een wielerwedstrijd in 1977 heeft men de hematocrietwaarde van een aantal wielrenners gemeten. Daarvan staan de meetresultaten in de volgende tabel.

Hematocrietwaarde	41	42	43	44	45	46	47	48	49
Frequentie	2	3	5	11	15	8	4	3	2

Hematocrietwaarde	50	51	52	53	54	55	56	57
Frequentie	1	0	0	1	2	0	0	1

Bereken de gemiddelde hematocrietwaarde van deze wielrenners.

Ook in 1988 en 1999 heeft men bij deze wielerwedstrijd van een aantal wielrenners de hematocrietwaarde gemeten.
In 1998 was de gemiddelde hematocrietwaarde 45,9.
De hematocrietwaarden uit 1999 zijn verwerkt in onderstaande boxplot.

Toon aan dat, op grond van de boxplot, de gemiddelde hematocrietwaarde in 1999 zeker groter was dan in 1998.

10.

examenvraagstuk HAVO wiskunde A, 2005.

Het aantal geldopnames en de grootte van de opgenomen bedragen variëren van geldautomaat tot geldautomaat. Het maakt natuurlijk uit waar de geldautomaat staat. Zo zal een geldautomaat in een stadscentrum dagelijks meer geldopnames hebben dan een geldautomaat in een dorp met weinig inwoners.
Hieronder staan twee boxplots die betrekking hebben op de opgenomen bedragen op een zekere dag bij twee geldautomaten in twee verschillende steden.

Hieronder staan drie uitspraken over deze boxplots.

Bij geldautomaat II is er die dag in totaal meer geld opgenomen dan bij geldautomaat I.

Het kleinste en het grootste bedrag dat die dag bij beide geldautomaten zijn opgenomen zijn hetzelfde.

Bij geldautomaat I worden relatief meer kleine bedragen opgenomen dan bij geldautomaat II.

Geef van elke uitspraak aan of deze is af te leiden uit de figuur. Licht je antwoorden toe.