|
|
 |
|
Spreidingsmaten. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
| Vorige les hebben we
gezien welke drie manieren er zijn om het "MIDDEN" van een verdeling aan
te geven; de modus, de mediaan en het gemiddelde. Maar het midden van
een verdeling zegt natuurlijk lang niet alles. Kijk naar de histogrammen
hieronder. Die hebben allemaal hetzelfde aantal metingen en dezelfde
mediaan en gemiddelde. (Degenen waar de modus bestaat hebben ook nog
eens dezelfde modus).Toch zijn ze nogal verschillend, vind je niet? |
| |
|
|
|
| |
|
Waar zit hem nou dat verschil in?
Het "midden" van deze verdelingen zit wel steeds op dezelfde plaats,
maar de spreiding eromheen is nogal verschillend. De
eerste drie hebben nog wel ongeveer dezelfde "vorm", maar de breedte is
enorm verschillend. De vierde heeft een heel andere vorm.
Er zijn verschillende manieren om de spreiding van een verdeling in een
getal uit te drukken. |
| |
|
|
1. De spreidingsbreedte. |
| |
|
De spreidingsbreedte is de allereenvoudigste.
Het is gewoon de breedte van het histogram, ofwel de grootste meting min
de kleinste.
Een voordeel is dat het zo'n makkelijk te berekenen getal is. Een groot
nadeel is echter, dat deze breedte nogal gevoelig is voor één kleine
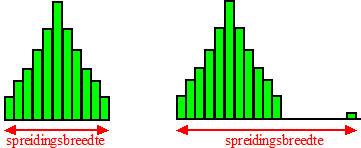
afwijking. Neem het histogram in de volgende figuren: |
| |
|
|
 |
| |
|
| Die ene kleine meting daar rechts
verandert de spreidingsbreedte heel spectaculair, terwijl de rest toch
gelijk is. |
| |
|
|
2. De kwartielafstand. |
| |
|
| Om dit laatste probleem op te
vangen, en zo'n paar kleine getallen aan de rand niet teveel invloed te
laten hebben, kunnen we afspreken om de buitenste getallen niet mee te
laten tellen. |
Je zou bijvoorbeeld kunnen afspreken om
alleen het middelste deel van de figuur te nemen, bijvoorbeeld de
middelste 50% van de metingen.
Verdeel je getallen in vier gelijke delen
(dat wil zeggen evenveel metingen in elk deel, dus 25% van je metingen) en neem dan de breedte
van de middelste twee stukken.
De grenzen waar 25%, 50% en 75% van je metingen geweest zijn heten de
kwartielen Q1, Q2 en Q3.
Overigens kennen wij dat tweede kwartiel Q2 ook al onder de
naam mediaan (het is immers waar de helft
van je metingen geweest is?) |
|
Als maat voor de spreiding nemen we nu de
middelste helft, dus dat is de afstand tussen Q1 en Q3.
Dat heeft als voordeel dat een paar lossen metingen aan de rand deze
spreiding niet beïnvloeden. Maar het heeft uiteraard als nadeel dat de
"vorm" en grootte van de buitenste helft helemaal niet worden meegeteld.
Twee voorbeelden van het berekenen van deze kwartielafstand: |
|
| |
|
Voorbeeld bij losse
getallen.
Stel dat we de getallen 2, 3, 3, 3, 5, 6, 6, 7, 8, 8, 8, 8, 9, 9,
10, 10, 10, 12, 13 hebben gemeten.
De mediaan is de middelste, en van 19 getallen is dat nummer 10, dus dat
is het getal 8.
We spreken nu af dat we deze mediaan niet weer meetellen voor de
berekenen van de kwartielen. Dat betekent dat de mediaan de getallen
verdeelt in twee groepen van negen: 2,3,3,3,5,6,6,7,8
en 8,8,9,9,10,10,10,12,13
(als de mediaan tussen twee getallen in had gezeten, dan hadden we dit
probleem niet gehad).
Het eerste kwartiel is nu de middelste van de eerste groep (de mediaan
van de eerste groep) en dat is Q1 = 5. En op dezelfde manier
is het tweede kwartiel de mediaan van de tweede groep en dat is Q3
= 10.
De kwartielafstand is dan gelijk aan Q3 - Q1
= 10 - 5 = 5
opm. Er zijn andere methoden om de kwartielen te
berekenen. We gebruiken deze methode mede omdat ook de TI-83 daarmee
rekent.
meer methoden kun je hier vinden. Het is maar wat je afspreekt....
|
| |
|
Voorbeeld bij
klassenindeling.
Bij klassenindelingen gaat het berekenen van de kwartielen eigenlijk
precies zo als het berekenen van de mediaan. Het enige verschil is dat
we nu bij 25% en 75% moeten kijken in plaats van 50%. Laten we de
kwartielafstand van de volgende verdeling berekenen. |
| |
| klasse |
[25, 33〉 |
[33, 41〉 |
[41, 49〉 |
[49, 57〉 |
[57, 65〉 |
[65, 73〉 |
| frequentie |
2 |
10 |
36 |
18 |
10 |
4 |
|
|
| |
In de cumulatieve frequentiepolygoon rechts
staan op de rechter verticale as de frequenties in procenten.
Q1 zit tussen de punten (41, 15%) en (49, 60%)
Dat is 45% totaal over een afstand van 8.
25% zit 10% vanaf het begin dus dat is afstand 10/45
• 8 = 1,8.
Dus Q1 = 41 + 1,8 = 42,8
Op dezelfde manier vind je de mediaan bij 50% (Med = 47,2) en het
derde kwartiel bij 75% (Q3 = 54,3) |
| De kwartielafstand is dus 54,3 - 42,8 =
11,5. |
|
| |
|
|
3. De gemiddelde deviatie. |
| |
|
Dit is een methode waarbij wél
elke meting meetelt. Het is erg eenvoudig, maar wel wat meer werk dan de
vorige methodes:
| |
| Bereken de gemiddelde afstand tot het
gemiddelde |
|
| |
|
Dus: eerst bereken je het
gemiddelde van alle metingen. Dan bepaal je van elke meting de afstand
(deviatie) die hij tot het midden heeft. (bij klassenindelingen doe je
weer alsof alle metingen in een klasse gelijk zijn aan het
klassenmidden)
Tenslotte neem je het gemiddelde van al deze deviaties.
Voorbeeld.
We hebben de metingen 3, 5, 5, 5, 7, 8, 8, 8, 8, 12, 15, 16, 20,
20, 20, 36.
Bereken de gemiddelde deviatie.
Het gemiddelde is (3 + 5 + 5 + 5 + 7 + 8 + 8 + 8 + 8 +
12 + 15 + 16 + 20 + 20 + 20 + 36)/16 = 12,25
De afstanden tot 12,25 zijn resp.:
9.25 - 7.25 - 7.25 - 7.25 - 5.25 - 4.25 - 4.25 - 4.25 - 4.25 - 0.25 -
2.75 - 3.75 - 7.75 - 7.75 - 7.75 - 23.75
Het gemiddelde van deze getallen is ongeveer 6,7 en dat is de
gemiddelde deviatie.
Voorbeeld.
Bereken de gemiddelde deviatie van de frequentieverdeling hieronder. |
| |
|
| meting |
[0, 8〉 |
[8, 16〉 |
[16, 24〉 |
[24, 32〉 |
[32, 40〉 |
[40, 48〉 |
[48, 56〉 |
| frequentie |
5 |
9 |
13 |
13 |
16 |
10 |
7 |
|
| |
|
De klassenmiddens zijn 4,
12, 20, ...
Het gemiddelde is (5 • 4 + 9 • 12 + 13 • 20 +
13 • 28 + 16 • 36 + 10 • 44 + 7 • 52)/(5
+ 9 + 13 + 13 + 16 + 10 + 7) = 29,21
Maak een nieuwe tabel met daarin de klassenmiddens en hun afstand tot
het gemiddelde: |
| |
|
| meting |
[0, 8〉 |
[8, 16〉 |
[16, 24〉 |
[24, 32〉 |
[32, 40〉 |
[40, 48〉 |
[48, 56〉 |
| midden |
4 |
12 |
20 |
28 |
36 |
44 |
52 |
| afstand tot 29,21 |
25,21 |
17,21 |
9,21 |
1,21 |
6,79 |
14,79 |
22,79 |
| frequentie |
5 |
9 |
13 |
13 |
16 |
10 |
7 |
|
| |
|
Het gemiddelde is dan:
(5 • 25,21 + 9 • 17,21 + 13 • 9,21 + 13 • 1,21 + 16
• 6,79 + 10 • 14,79 + 7 • 22,79)/(5 + 9
+ 13 + 13 + 16 + 10 + 7) = 11,4 |
| |
|
|
 |
|
|
 |
|
modus, mediaan,
gemiddelde |
|
|
boxplot |
|
| |
|
| 1. |
Bereken van de volgende serie getallen de
spreidingsbreedte, de kwartielafstand en de gemiddelde deviatie: |
| |
|
|
|
| |
35, 35, 35, 38, 42, 42, 42, 42, 56, 67, 67, 68,
70. |
| |
|
|
|
| 2. |
Bereken van de volgende frequentieverdeling de
spreidingsbreedte, de kwartielafstand en de gemiddelde deviatie: |
| |
|
|
|
| |
| meting |
[5, 17〉 |
[17, 29〉 |
[29, 41〉 |
[41, 53〉 |
[53, 65〉 |
[65, 77〉 |
[77, 89〉 |
| frequentie |
12 |
35 |
58 |
123 |
88 |
73 |
22 |
|
| |
|
|
|
| 3. |
Hiernaast staat een cumulatief
frequentiepolygoon van de leeftijden van alle leden van een
golfvereniging.
Bepaal met dit polygoon de kwartielafstand, de mediaan en de
modus van deze metingen. |
|
| |
|
 4. 4. |
Van een steekproef van 5 waarden is het gemiddelde 10 en is de mediaan 12.
Wat is de kleinst mogelijke spreidingsbreedte in deze steekproef ? |
| |
|
|
|
| 5. |
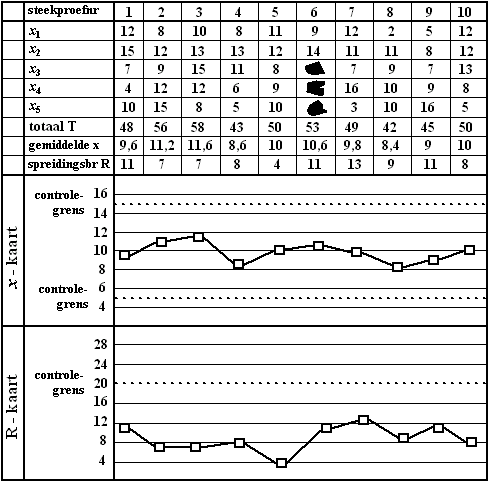
Examenvraagstuk VWO Wiskunde A,
2001 Bij een steekproef zakken suiker bepaalt men het
gemiddelde gewicht x en de spreidingsbreedte R (dat is het
verschil tussen de grootste en de kleinste meting).
Men noteert al deze gegevens op een controlekaart, de x/R-kaart.
Op de x/R-kaart hieronder staan de meetresultaten van 10
steekproeven.
Iedere steekproef bestaat uit 5 zakken. Op de controlekaart worden de
afwijkingen van 500 gram bij ieder van deze zakken genoteerd als x1,
x2, x3, x4 en x5.
Zo heeft de derde zak van de tweede steekproef een gewicht van 509 gram.
Dit is genoteerd als 9.
Het gemiddelde van de eerste steekproef is 509,6 gram. Dit wordt dan
genoteerd als 9,6.
De spreidingsbreedte van de eerste steekproef is 515 - 504 = 11 gram. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Bij steekproef nr. 6 zijn enkele gegevens
onleesbaar geworden. |
| |
|
|
|
| |
a. |
Welke getallen kunnen hier bijvoorbeeld gestaan hebben?
Licht je antwoord toe. |
| |
|
|
|
| |
Bij de controle van het vulproces met
behulp van de x/R-kaart let men erop of x of R de zogeheten
controlegrenzen overschrijden. Deze controlegrenzen zijn in de grafieken
met stippellijnen aangegeven. Zodra bij een steekproef een van deze
grenzen overschreden wordt slaat men alarm.
Op een gegeven moment slaat men alarm bij een steekproef terwijl met de
waarde van x niets mis is. |
| |
|
|
|
| |
b. |
Wat zouden de vijf gewichten in deze steekproef
bijvoorbeeld kunnen zijn? Licht je antwoord toe. |
| |
|
|
|
| 6. |
Examenopgave HAVO wiskunde A, 2022-II |
| |
|
|
|
| |
Wanneer er een melding bij de
ambulance-meldkamer binnenkomt, moet men de mate
van urgentie van de melding vaststellen en zorgen voor de inzet van
een ambulance: een ambulancerit. De mate van urgentie kan zijn: |
| |
- |
Hoge urgentie:
de benodigde zorg is spoedeisend en er is sprake van direct
levensgevaar voor de patiënt. We noemen dit een A1-rit. |
| |
- |
Lage urgentie:
de benodigde zorg is spoedeisend, maar er is geen direct
levensgevaar voor de patiënt. We noemen dit een A2-rit. |
| |
- |
Geen urgentie:
de benodigde zorg is niet spoedeisend. We noemen dit een B-rit. |
| |
|
|
|
| |
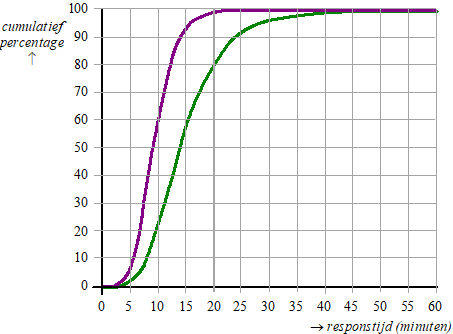
In de rest van
de opgave kijken we alleen naar A1-ritten en A2-ritten. Omdat er bij
A1-ritten sprake is van direct levensgevaar voor de patiënt, zijn de
responstijden van deze ritten over het algemeen korter dan de
responstijden van de A2-ritten.
In de figuur staan de relatieve cumulatieve frequentiepolygonen van
de responstijden van de A1-ritten en die van de responstijden van de
A2-ritten in 2014. In de figuur is niet aangegeven welke polygoon
bij de A1-ritten hoort en welke bij de A2-ritten. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Bepaal met
behulp van de figuur de interkwartielafstand van de responstijd van
de A1-ritten. Geef hierbij aan welke polygoon je gebruikt hebt en
licht je keuze toe. |
| |
|
|
|
|
| |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|