standaarddeviatie


De Standaarddeviatie.	© h.hofstede (h.hofstede@hogeland.nl)

We hebben al gezien dat spreidingsmaten aangeven hoe ver de gemeten getallen uit elkaar liggen. Daarvoor hebben we al de spreidingsbreedte de kwartielafstand en de gemiddelde deviatie behandeld. Maar er is nog een andere, veel meer gebruikte maat voor de spreiding, en dat is de standaarddeviatie (of ook wel de standaardafwijking).

De letter die we daarvoor gebruiken is σ.

De berekening daarvan lijkt nogal op die van de gemiddelde deviatie, maar je moet net één stapje extra doen.
Het recept ervoor is als volgt:

Oh ja; waarschijnlijk had je het al wel verzonnen hoop ik: als je te maken hebt met een klassenindeling, dan doe je weer alsof alle metingen in een klasse gelijk zijn aan het klassenmidden.

Vergeleken met de "gewone" gemiddelde deviatie zijn die stap 3 en stap 5 dus nieuw. Het lijkt nogal vreemd: je neemt eerst van al die afwijkingen het kwadraat, en na afloop van al die gemiddelde kwadraten weer de wortel.

σ = standaarddeviatie
= √(gemiddelde kwadratische afwijking)

Wat heeft dat voor zin?

Dat heeft in ieder geval twee simpele praktische voordelen.
Op de eerste plaats hoeven we ons er niet meer druk om te maken of de afwijking tot het gemiddelde nou plus of min is. Door dat kwadraat wordt alles gewoon plus, en dat maakt onze formules veel eenvoudiger.
Op de tweede plaats heeft dat kwadraat nemen tot gevolg dat de getallen die verder van het midden afliggen ook zwaarder meetellen, en dat willen we ook graag immers die zeggen meer over de spreiding.

Er is ook nog een minder simpel praktisch voordeel.

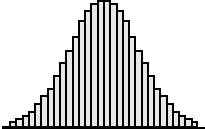
Het blijkt in praktijk dat histogrammen er vaak ongeveer zo uitzien als hiernaast. Veel metingen zijn ongeveer gelijk aan het gemiddelde en steeds minder metingen zitten verder van het midden af.
Dit histogram heet de normale verdeling en de "breedte" daarvan blijkt makkelijk te beschrijven met de standaarddeviatie.

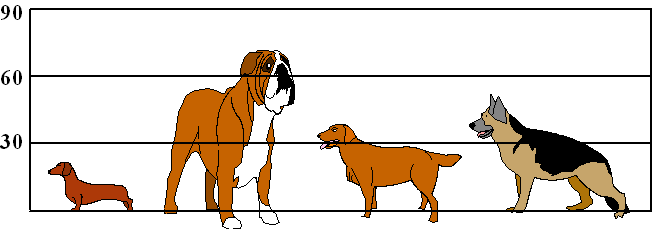
Voorbeeldberekening.

Vier hondenliefhebbers vergelijken de hoogte van hun honden:

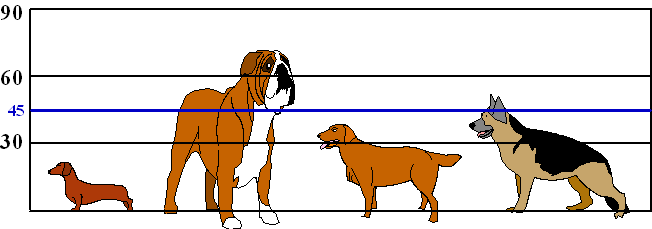
Ze meten achtereenvolgens de hoogtes 19 cm, 70 cm, 39 cm en 55 cm.
De gemiddelde hoogte is dan 45 cm, en dat geeft de blauwe lijn hieronder aan

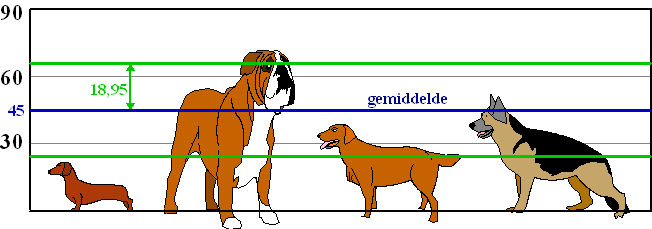
De afwijkingen van de vier honden ten opzichte van dat gemiddelde zijn 26 cm, 25 cm, 6 cm en 10 cm.
De kwadraten daarvan zijn 676, 625, 36 en 100
Het gemiddelde van deze vier kwadraten is ^{(676 + 625 + 36 + 100)}/₄ = 359,25
De wortel daarvan is √359,25 ≈ 18,95 cm.
Hieronder kun je zien wat die spreiding van 18,95 cm ten opzichte van het gemiddelde van 45 cm betekent.

De beide groene lijnen liggen op afstand 18,95 cm vanaf het gemiddelde.
Je ziet dat de laatste twee honden minder dan een standaarddeviatie van het midden af zitten.

In de tabel hiernaast is nog eens schematisch te zien hoe de berekening van de standaarddeviatie in zijn werk is gegaan.

hond nr.	hoogte (cm)	afw. Δ	Δ²
1 2 3 4	19 70 39 55	26 25 6 10	676 635 56 100
gem. 45			gem.359,25
gem. 45			σ = 18,95

Wat stelt het ongeveer voor?

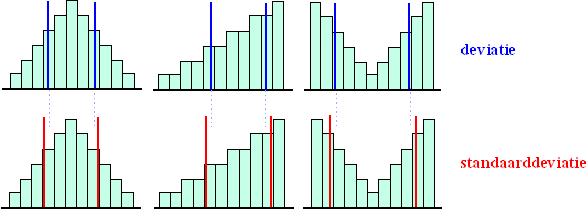
Hieronder zijn voor een aantal histogrammen in dezelfde figuur de standaarddeviatie en de gemiddelde deviatie als afstand vanaf het gemiddelde gegeven. De blauwe en rode lijnen hieronder geven steeds de plaats van gemiddelde-plus-deviatie/standaarddeviatie en gemiddelde-min-deviatie/standaarddeviatie.

Je ziet dat het allemaal niet spectaculair veel verschilt van elkaar. De standaarddeviatie bestrijkt steeds een iets breder deel van het histogram dan de "gewone"deviatie. Dat komt natuurlijk omdat die buitenste meetwaarden wat zwaarder meetellen.

Formules....
Als je geïnteresseerd bent in formules, dan kun je in de verdieping hiernaast wat formules voor de standaarddeviatie vinden. Veel zul je ze niet gebruiken; meestal wordt de standaarddeviatie met een computer/rekenmachine berekend.


boxplot			verdelingen veranderen

Met de TI-83

Nou, dat gaat precies zo als de berekeningen van het gemiddelde en de mediaan en de kwartielen.

Voer de frequentieverdeling in in je TI via STAT - EDIT

Bedenk wel dat je bij een klassenindeling de klassenmiddens moet gebruiken in L1.

Gebruik daarna STAT - CALC - 1: 1-Var Stats ( L1 , L2 ) waarbij in L1 de meetwaarden (evt klassenmiddens) staan en in L2 de frequenties (of procenten). L1 en L2 vind je boven de knoppen 1 en 2 (dus 2nd gebruiken).

In het lijstje dat je dan voor je neus krijgt is σx de standaarddeviatie.

Voor de volgende tabel zie daaronder hoe dat er op de TI-83 uitziet.

meetwaarde	2 -< 10	10 -< 18	18 -< 26	26 -< 34	34 -< 42
frequentie	6	13	27	23	12

Zoals je ziet komen in L1 de klassenmiddens (als dat nodig is)
rechts zie je dat de standaarddeviatie gelijk is aan 8,978.....

De standaarddeviatie van een rij losse getallen.

Natuurlijk kun je ook van een rij "losse" getallen de standaarddeviatie berekenen.
Volgens bovenstaande methode zou je de getallen in L1 moeten zetten allemaal met frequentie 1 in L2, immers elk gsetal komt één keer voor.
Maar je rekenmachine kan dat sneller....
Als je je getallen in L1 zet, en dan eenvoudig gebruikt STAT - CALC - 1-Var-Stats (L1) dan neemt je rekenmachine automatisch alle frequenties gelijk aan 1. Dat scheelt weer een boel enen in vullen......

De standaarddeviatie van een kansverdeling.
.....die kun je in deze les vinden......

OPGAVEN

Een atlete heeft tijdens 10 achtereenvolgende trainingen steeds direct na een 400-meterloop haar polsslag gemeten.
Dat leverde de volgende serie waarden op:

100 - 112 - 120 - 105 - 145 - 132 - 110 - 156 - 194 - 134

Bereken de standaarddeviatie van deze waarden.

≈27,13

De waarde 194 is wel érg hoog. De atlete vermoedt daarom dat zij een meetfout heeft gemaakt. Hoe groot zou de standaarddeviatie zijn geweest zonder deze meetwaarde?

≈18,02

In de volgende tabel staan de hoogten van een groot aantal bomen in een bos.

hoogte	4-<8	8-<12	12-<16	16-<20	20-<24	24-<28	28-<32	32-<36	36-<40
frequentie	14	20	36	58	43	22	12	8	2

Bereken de standaarddeviatie van deze hoogten.

≈6,95

Hoeveel procent van de bomen heeft een hoogte die niet meer dan één keer de standaarddeviatie van het gemiddelde afwijkt?

≈68,7%

Hoe groot zou de standaardafwijking zijn als een klassenbreedte van 8 was gekozen in plaats van 4?
Bereken dat voor het geval de eerste klasse gelijk is aan 0-<8 en ook bij 4-<12

7,20 en 7,36

Voor een aantal scholen is het aantal leerlingen dat zij hebben geteld. Dat leverde de tabel hiernaast.

aantal leerlingen	aantal scholen
100 - 299	31
300 - 499	50
500 - 699	56
700 - 899	80
900 - 1099	108
1100 - 1299	100
1300 - 1499	76
1500 - 1699	75

Bereken van deze frequentieverdeling het gemiddelde en de standaarddeviatie. Rond af op gehele getallen.

Bereken hoeveel scholen er méér dan de standaarddeviatie van het gemiddelde afliggen. (neem aan dat de scholen gelijkmatig over de klassen zijn verdeeld)

Maak een nieuwe klassenindeling met een breedte van 400, en bereken opnieuw het gemiddelde en de standaarddeviatie. Bereken opnieuw het gemiddelde. Leg uit waarom dit veranderd is. Tussen welke grenzen kan het gemiddelde van bovenstaande frequentieverdeling liggen?

Pakken suiker worden meestal verkocht in hoeveelheden van 1000 gram. Maar de vulmachine zal echt niet heus precies 1000 gram in een pak doen. In werkelijkheid fluctueert de inhoud van een pak een beetje. In de volgende tabel staat de inhoud van 30 pakken suiker (in grammen).

1000 1008   1004     995   996   998   1003   1004     999 1001
993    998   1005   1005   998   995   1002   1000   1004    997
998 1002   1009     994   998   999   1000   1000   1001 1005

Bereken het gemiddelde en de standaarddeviatie van deze gewichten.

1000,37 en 3,94

Hoeveel procent van de pakken heeft een gewicht dat méér dan een standaarddeviatie van het gemiddelde afwijkt?

In het dubbele steel- en bladdiagram hiernaast staan de proefwerkcijfers van een klas, gesplitst naar meisjes en jongens.

Probeer zonder een berekening te maken in te schatten wie de grotere standaarddeviatie heeft (de jongens of de meisjes).

Controleer je antwoord op de vorige vraag met een berekening.

Ga met een berekening na of de standaarddeviatie van de hele groep jongens en meisjes sámen gelijk is aan de standaarddeviatie van de jongens plus die van de meisjes.

Iemand heeft een nogal saai histogram: het bestaat uit allemaal even hoge staven met elk breedte 1. Hij weet alleen niet meer hoeveel staven er nou precies waren, maar nog wel dat de standaarddeviatie van zijn metingen gelijk was aan 3,74.

Leg uit waarom de precieze hoogte van al die staven er niet toe doet voor de standaarddeviatie.

Leg uit dat de standaarddeviatie groter wordt als het aantal staven groter wordt.

Bepaal uit hoeveel staven zijn histogram bestond.

Hiernaast staat de frequentietabel van de maandinkomens van de werknemers van een groot bedrijf.

inkomen	aantal
1000 - < 1200	860
1200 - < 1800	340
1800 - < 2800	600
2800 - < 3600	450
3600 - < 4000	200
4000 - < 5000	380

Maak hiervan een histogram. Gebruik op de y-as een frequentiedichtheid..

Hoeveel procent van de werknemers heeft naar schatting een inkomen dat niet meer dan één standaarddeviatie van het gemiddelde afwijkt?

69%