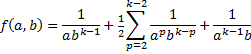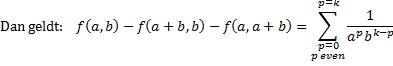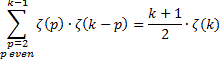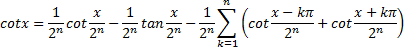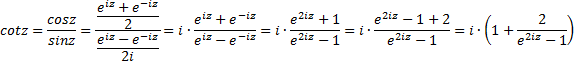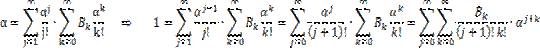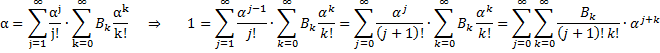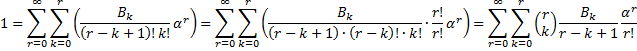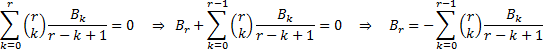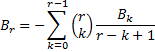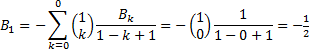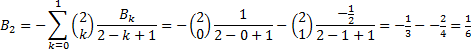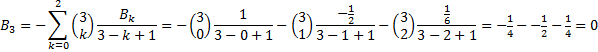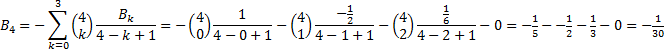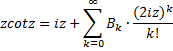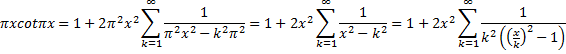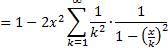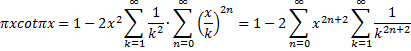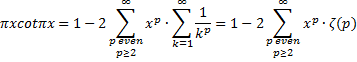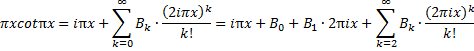| ζ(2), ζ(4), ζ(6), ... | |||||||||||||||||||||||||||||
| In de vorige les
zagen we de geweldige manier waarop Euler
ζ(2)
berekende (π²/6
weet je nog?) Deze les gaan we op zoek naar andere waarden van de functie ζ(x). |
|||||||||||||||||||||||||||||
| 1. Een soort van recursievergelijking. | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Dat kun je zelf makkelijk nagaan door al die breuken samen te nemen en de haakjes weg te werken. 't Is nogal een omslachtig en saai werkje en als je het echt niet gelooft, kijk dan maar in het bewijs hiernaast. | |||||||||||||||||||||||||||||
Ik ga intussen verder..... |
|
||||||||||||||||||||||||||||
| Als je nou die
rechterkant sommeert over alle mogelijke ab-koppeltjes (a,
b > 0) dan gebeurt er iets leuks. Kijk maar als je ze allemaal gaat opschrijven: (f11 - f21 - f12) + (f12 - f32 - f13) + (f13 - f41 - f14) + (f14 - f54 - f15) + ... +(f21 - f31 - f23) + (f22 - f42 - f24) + (f23 - f53 - f25) + (f24 - f64 - f26) + ... + (f31 - f41 - f34) + (f32 - f52 - f35) + (f33 - f63 - f36) + (f34 - f74 - f37) + ... + ... Elke fab met a en b ongelijk komt er twee keer in voor: één keer "gewoon als fab" met een plusteken en één keer als fp+b,b of fa,a+p met een minteken (de eerste als b kleiner dan a is, de tweede als a kleiner dan b is). Ik heb er hierboven een paar gekleurd. Zo staat bijvoorbeeld f47 er voor a = 4 en b = 7 met een plusteken maar ook als f4,4+3 met een minteken. Dat valt allemaal tegen elkaar weg. De enigen die overblijven zijn dan f11 , f22, f33, f44... want die komen alleen als fab met een plusteken voor. Conclusie: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Maar omdat dat deel onder die som ook gelijk is aan 1/a²b² staat daar ook (ζ(2))2 , kijk maar: | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| En als je nou die
haakjes wegwerkt komt elk koppeltje 1/a²
• 1/b²
precies één keer voor. Conclusie: (ζ(2))2 = 5/2ζ(4) ofwel ζ(4) = 2/5 • ζ(2)2 = 2/5 • (p²/6)2 = 1/90 • π4 |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| En nu is de
uitbreiding naar hogere even waarden van
ζ(x)
ook te doen. Op jacht naar ζ(6) definiëren we de volgende functie |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Je houdt elke keer
alleen de
koppeltjes met even machten over!!! Beide kanten sommeren over alle ab-koppeltjes geeft, net als hierboven ζ(2) • ζ(4) + ζ(4) • ζ(2) = 7/2 • ζ(6) Daaruit volgt ζ(6) = 2/7 • 2 • 1/6p2 • 1/90π4 = 1/945 • π6 |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Het algemene geval
dan maar? Definieer voor het berekenen van ζ(k) de functie: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Dat geeft de volgende recursieve formule voor ζ(k): (als k even is) | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Dat geeft
bijvoorbeeld voor k = 8 direct
ζ(2)ζ(6)
+
ζ(4)ζ(4) +
ζ(6)ζ(2) =
9/2
•
ζ(8) 1/6π2 • 1/945 • π6 + 1/90 • π4 • 1/90 • π4 + 1/945• π6 • 1/6π2 = 9/2 • ζ(8) 64/2835 • π8 = 9/2 • ζ(8) ζ(8) = π8/9450 |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| En zo verder.... | |||||||||||||||||||||||||||||
| 2. Is er niet een directe formule mogelijk? Dat heb ik liever! | |||||||||||||||||||||||||||||
| Zeker is dat
mogelijk, maar daarvoor moeten we wel wat werk verrichten. Oké, ik zit
een beetje op te scheppen: dit werk is allemaal al door Euler verricht,
en ik hoef hem alleen maar braaf te volgen. STAP 1: COTANGENS. Eerst maakte Euler een formule voor de cotangens. Die heeft namelijk een leuke eigenschap.... Omdat cotx = 1/tanx kun je de verdubbelingsformule van tanx gebruiken (opgave 4 uit deze les): |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Zo kun je een
cotangens splitsen in twee delen met elk de halve hoek. Maar dat tangens-deel kun je weer omzetten in een cotangens: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Als je nou (1) en (2)
samen gebruikt kun je een cotangens splitsen in twee delen, en dan van
dat tangensdeel weer een cotangens maken, en dan die cotangensdelen wéér
splitsen, enz. Dan krijg je het volgende vermakelijke rijtje: |
|||||||||||||||||||||||||||||
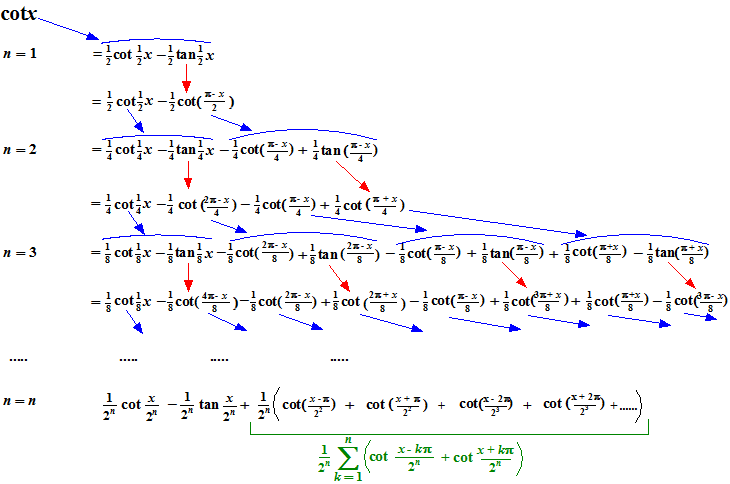 |
|||||||||||||||||||||||||||||
| Bij die blauwe pijlen
splitst een cotangens zich in twee delen met elk de halve hoek. Bij die rode pijlen wordt een tangens omgezet in een cotangens. Bij die laatste stap is verder gebruikt dat -cot(α) = cot(-α) om de mintekens in plussen te veranderen. Dat levert de volgende prachtige formule op: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Vervolgens liet Euler
n naar oneindig gaan. Dan gaat x/2n
naar nul, want x is een eindig getal. Laten we dan één voor één de drie termen van de rechterkant van deze vergelijking eens wat beter bekijken. Noem dat stukje x/2n even α, dan geeft dat: |
|||||||||||||||||||||||||||||
|
• |
|
||||||||||||||||||||||||||||
| Als a naar nul gaat, dan gaat α/sinα naar 1, en cosα ook, dus van deze term blijft alleen 1/x over. | |||||||||||||||||||||||||||||
|
• |
|
||||||||||||||||||||||||||||
| Als a naar nul gaat, dan gaat sinα naar 0, en cosα naar 1 dus deze term gaat naar nul. Mooi, dat ruimt lekker op. | |||||||||||||||||||||||||||||
|
• |
Nou die lastige som
nog..... Maar wacht eens even.... we kunnen daarvoor dezelfde truc als bij de eerste term gebruiken. Als α naar nul gaat, dan gaat α • cotα kennelijk naar 1 dus cotα gaat naar 1/α!!! Dat betekent dat cot((x - kπ)/2k) nadert naar 2k/(x - kπ) en cot((x + kπ)/2k) nadert naar 2k/(x + kπ) |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Die 2n valt nog weg tegen de 2n voor de som, dus dan blijft uiteindelijk over: | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| STAP 2. BERNOULLI GETALLEN | |||||||||||||||||||||||||||||
| Vervolgens ging Euler
kijken of hij niet ook op een andere manier een formule
voor cotangens kon maken, zodat hij daarna die formules met elkaar kon
vergelijken (dat was trouwens één van de favoriete methodes van Euler).
Dat speelde hij klaar door over te stappen op complexe getallen, want Euler had vrij veel verstand van complexe getallen en wist namelijk al hoe hij van cosz en sinz machten van e kon maken. Dat ging zó: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Als je dit nou met z vermenigvuldigt dan geeft dat: | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Daar helemaal rechts
staat nu α/(ea
- 1) (met α = 2iz)
en dat is een functie waar je een Taylorreeksontwikkeling van kunt
maken. Laten we er een paar termen van uitrekenen...... |
|||||||||||||||||||||||||||||
| • |
|
||||||||||||||||||||||||||||
| • |
|
||||||||||||||||||||||||||||
| Daar was al twee keer
l'Hopital nodig... Plus de nodige differentieerregels. Het wordt wel weg snel ingewikkelder, vind je niet....?? |
|||||||||||||||||||||||||||||
| Hmmm....Misschien kunnen we beter achteraan beginnen en dan terugwerken... | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Die getallen Bk
zijn voorlopig nog onbekende constanten (alhoewel we al weten dat B0
= 1 en B1 = -1/2) In de formule vervangen we eα vervangen door zijn Taylorreeks S(αk/k!) en door die -1 die erbij staat loopt de reeks nu vanaf 1 tot oneindig (in plaats van vanaf 0). Daarna delen we beide kanten door α. Dat geeft: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
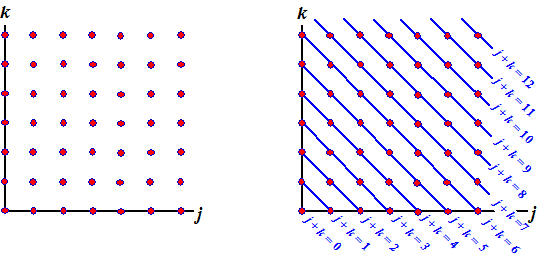
| We moeten nu sommeren over alle gehele waarden van de koppeltjes ( j , k) Dus eigenlijk alle roosterpunten van het vlak langslopen. Dat gaan we handig op een andere manier doen, zoals hieronder is getekend, | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| In de rechterfiguur
lopen we de punten van het vlak per rechte blauwe lijn j
+ k = r langs. Als we dan alle waarden van r nemen en alle
punten van zo'n lijn dan krijgen we ook precies alle punten één keer. Op
één zo'n blauwe lijn loopt k dan van 0 tot r en is
j gelijk aan r - k. Dat geeft voor de sommatie: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Daarin is gebruikt
dat (r - k + 1)! = (r - k + 1) • (r
- k)! om er mooie combinaties van te maken. Dat laatste moet je zó lezen: |
|||||||||||||||||||||||||||||
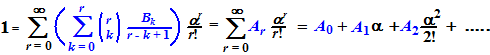 |
|||||||||||||||||||||||||||||
| Dat blauwe stukje is
het gedeelte dat van k afhangt, dus het deel dat je moet
sommeren. Als daar voor elke α steeds 1 uit moet komen, dan moet die eerste A0 gelijk zijn aan 1, en al die andere A's gelijk zijn aan nul. A0 = 1 betekent dat B0 = 1 (neem in het blauwe stukje r = 0 en k = 0) Dat die andere A's gelijk moeten zijn aan nul zegt dan eindelijk iets over de Bk's. Kijk maar (voor r > 0): |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| YES!!! Daar staat dan eindelijk een recursievergelijking om een nieuwe Br uit de vorige B's te berekenen! Belangrijk genoeg voor een kadertje: |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Meteen maar even uitproberen zou ik zeggen. Te beginnen met B0 = 1: | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| ....phew... ik kneep hem wel even moet ik eerlijk zeggen... maar gelukkig: onze berekeningen lijken te kloppen! | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Kijk: dat
gaat toch een stukje sneller dan via al die afgeleiden met de
Taylorreeks! Hier zijn een aantal Bernoulli getallen: |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Merk alvast even op
dat de oneven Bernoulligetallen B3, B5,
B7, ... allemaal gelijk zijn aan nul. Dat gaan we later nog
gebruiken. Dat dat inderdaad zo is kun je makkelijk zien door de B1-term
van de reeksontwikkeling (-1/2x)
naar de andere kant te brengen. Dat geeft de functie f(x) = x/(ex - 1) + 1/2x en die kun je zó anders schrijven: |
|||||||||||||||||||||||||||||
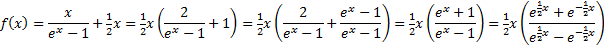 |
|||||||||||||||||||||||||||||
| In die laatste stap
zijn teller en noemer gedeeld door e½x
. Als je in die laatste formule x vervangt door -x dan blijft het resultaat gelijk. Dat betekent dat f(x) een even functie is, dus dat alle coëfficiënten van de oneven machten van x in de reeksontwikkeling gelijk zijn aan nul. Dat zijn inderdaad precies de B3, B5, B7, .... |
|||||||||||||||||||||||||||||
| STAP 3. NOU NOG EVEN COMBINEREN | |||||||||||||||||||||||||||||
| Even samenvatten wat we in stap 1 en stap 2 hebben ontdekt: | |||||||||||||||||||||||||||||
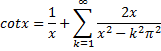 |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| En daarbij is nog steeds de grote vraag: | |||||||||||||||||||||||||||||
|
Wat heeft dit in vredesnaam met ζ(s) te maken? |
|||||||||||||||||||||||||||||
| Nou, het antwoord op die vraag verschijnt vanzelf als je xcotx met de bovenste van de twee formules gaat uitschrijven, maar dan met in plaats van x nu πx | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Daar helemaal op het eind, die laatste breuk, dat is een oude bekende: de som van een meetkundige reeks! | |||||||||||||||||||||||||||||
|
Snel bewijsje tussendoor S = 1 + x + x2 + x3 + .... xS = x + x2 + x3 + x4 van elkaar aftrekken: S(1 - x) = 1 dus S = 1/(1 - x) Het schijnt namelijk didactisch verantwoord te zijn om bij moeilijke stof af en toe iets makkelijks tussendoor te laten zien zodat iedereen denkt "Hé, dit kan ik best volgen....dan is de rest vast ook te doen....J" |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Als je nu 2n + 2 een nieuw even getal p noemt dan loopt p van 2 tot oneindig als n van 0 tot oneindig loopt. Maar wel alleen langs alle even getallen. | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Daar verschijnt dan
eindelijk.... eindelijk.... eindelijk.... onze zetafunctie! Meteen maar proberen ook πxcotπx in de tweede formule te gebruiken: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Omdat B0 =
1 en B1 = -1/2
kloppen de coëfficiënten van x0 en x1
in beide cotangensformules met elkaar. Da's dan weer mooi. | Maar ook de andere coëfficiënten moeten gelijk zijn Kijk naar de coëfficiënt van xp in beide formules. Dat is de coëfficiënt van x2k in de laatste vergelijking want p moet even zijn, dus p = 2k. Dat betekent dat -2ζ(2k) = B2k • (2πi)2k/(2k)! en omdat i2k = (i2)k = (-1)k geeft dat het volgende resultaat |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| En daarmee is de
directe formule gevonden. Merk nog even op dat coëfficiënten van
x3, x5, .... in beide
cotangensformules gelijk zijn aan nul. In die eerste formule omdat die
daar gewoonweg niet in voorkomen, in de tweede formule omdat B3
= B5 = .... = 0 Nou, meteen maar even een paar ζ(s) uitrekenen, we hebben de formule niet voor niets afgeleid: |
|||||||||||||||||||||||||||||
| • |
|
||||||||||||||||||||||||||||
| • |
|
||||||||||||||||||||||||||||
|
• |
|
||||||||||||||||||||||||||||
| enz. Precies zoals we recursief ook al hadden gevonden...... | |||||||||||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||||||||||||||||||