© h.hofstede (h.hofstede@hogeland.nl)
Som-en Verschilformules voor sinus en cosinus.

soscastoa

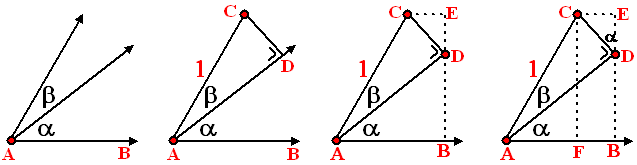
Bekijk de figuur hierboven.
Eerst zijn twee willekeurige hoeken α en β getekend op een lijnstuk AB.
Daarna wordt op de bovenste lijn een lengte AC = 1 afgemeten, en er wordt een loodlijn CD op AD getekend.
Dat geeft samen de derde figuur.
In de laatste figuur is de loodlijn CF op AB getekend.

Nu geldt:  sin (α + β) = CF/1 = CF = DB + ED = sinα • AD  + cosα • CD = sinαcosβ + cosαsinβ
YES! we hebben een formule gevonden:

  sin(α + β) = sinαcosβ + cosαsinβ
Maar als α en β willekeurig zijn, dan mag je ze ook wel door iets anders vervangen.
Eigenlijk staat er: 

Daarbij mogen dat driehoekje en dat blokje dus alles zijn.
Laten we daar wat mee experimenteren.
Neem bijvoorbeeld   Δ = α en  ■ = -β, dan staat er:
sin(α - β) = sinαcos(-β) + cosαsin(-β)
maar omdat we al eerder vonden  (met die eenheidscirkel weet je nog?)  dat  cos(-β) = cosβ  en  sin(-β) = -sinβ geeft dat:  sin(α - β) = sinαcosβ - cosαsinβ. Yes! alweer een formule. Dat zijn er al twee.
1. Neem nu  Δ = 1/2π - α  en   ■ = -β
a. Toon aan dat de eerste formule dan verandert in  cos(α + β) = cosαcosβ - sinαsinβ
b. Vervang in deze laatste formule weer β door (-β) en maak een formule voor cos(α - β)

sin(α + β) = sinαcosβ + cosαsinβ
sin(α - β) =  sinαcosβ  -  cosαsinβ
cos(α + β) = cosαcosβ -  sinαsinβ
cos(α  - β) = cosαcosβ + sinαsinβ
2. Toon aan dat  sin2(α + 1/4π) = 1/2 + sinαcosα
3. Toon aan dat  cos(α + 1/6π) + cos(α - 1/6π) = √3 • cosα
   
4. Toon aan dat  cos2(1/4π - 1/2x) = 1/2 + 1/2sinx
5. 5/12 kun je schrijven als 3/12  + 2/12
Gebruik dat gegeven om aan te tonen dat  sin(5/12π) = 1/4√6 + 1/4√2.
6. a. Als je je beseft dat 1/12 = 1/4 - 1/6 dan kun je cos 1/12π berekenen. Doe dat.
b. Vergelijk je antwoord op vraag a) met dat op vraag 5 en geef een verklaring.
     
7. Het blijkt dat   cos2x + cos2(x - 1/3π) = 3/4 + cosx • cos(x - 1/3π)

Toon dat aan.
8.
Bereken het vraagteken in de figuur hiernaast.

TIP: Gebruik daarbij de formule voor cos(α + β) en natuurlijk Pythagoras.

 

75/(3√24 - 4) - √24
   
9. Het blijkt dat    1/2sinx - 1/6sin3x   een primitieve is van  sinxsin2x
Toon dat aan. Bedenk daarbij dat je cos(3x) kunt schrijven als cos(x + 2x)
   
Hulpje bij het Primitiveren.
   
Door deze som- en verschilformules handig te gebruiken kun je een aantal primitieven vinden.
Als je bijvoorbeeld die van sin(α + β) en sin(α - β) bij elkaar optelt dan krijg je:
sin(α + β) + sin(α - β) =  2sinαcosβ en daaruit volgt   sinαcosβ = 1/2(sin(α + β) + sin(α - β))
Dat geeft een mogelijkheid om sinαcosβ te primitiveren:

Voorbeeld.  Primitiveer de functie f(x) = sin2x• cos5x 
Met bovenstaande regel is   sin2x• cos5x = 1/2(sin7x + sin(-3x)) = 1/2(sin7x - sin3x)
De primitieve is dan F(x) = -1/14cos7x  + 1/6cos3x + c
   
10. Geef  primitiveerhulpjes voor de vormen   sinαsinβ  en cosαcosβ.
   
11. Gegeven is de functie  f(x) = sin2x • cos3x   met domein [0, 2π]
     
  a. Bereken algebraïsch de nulpunten van de grafiek van f.
   
x = k • 1/2π
x = 1/6π + k • 1/3π
  b. Toon aan dat de grafiek van f symmetrisch is in het punt (π, 0).
     
  c. Bereken algebraïsch de oppervlakte van het vlakdeel V, ingesloten door de grafiek van f en de x- as tussen x = 1/6π en x = 1/2π.
   

0,3√3
     
12. (Voor deze opgave moet je kunnen differentiëren)

Gegeven zijn op [0, 2π] de functies  f(x) = 2sin(x - 1/3π) en  gp(x) = psinx - p
     
  a. Los algebraïsch op:  f(x) > g1(x). Geef je antwoord in twee decimalen nauwkeurig.
   

[0.96 , 5.33]
  b. Bewijs dat f(x) en g2(x) elkaar raken en geef de coördinaten van hun raakpunt.
     
 
   

© h.hofstede (h.hofstede@hogeland.nl)