scheve asymptoten


Scheve Asymptoten (1).	© h.hofstede (h.hofstede@hogeland.nl)

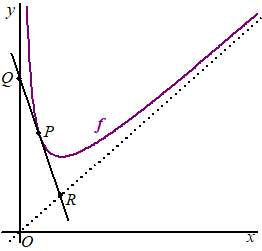
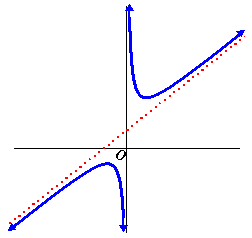
Bekijk de grafiek van de functie f(x) = 2x + ⁴/_x + 3 hiernaast.
Zoals (hopelijk) verwacht heeft de grafiek een verticale asymptoot bij x = 0. Maar als je goed naar de grafiek kijkt is er ook een scheve rechte lijn waar de grafiek langs gaat lopen (de rode stippellijn). Jawel: deze grafiek heeft een scheve asymptoot!

De vraag is: kunnen we dat aan het functievoorschrift al zien, en kunnen we misschien ook een vergelijking van deze scheve asymptoot opstellen?

De oplossing van beide vragen ligt hem in het feit, dat het gedeelte ⁴/_x voor grote x-waarden heel snel erg klein wordt.
Van de vergelijking y = 2x + ⁴/_x + 3 blijft voor hele grote x-waarden eigenlijk alleen nog maar het deel y = 2x + 3 over. De ⁴/_x is te verwaarlozen. Dat betekent dat de grafiek van deze functie er voor grote x-waarden uit zal zien als de grafiek van y = 2x + 3 en voilá; dat is dus de vergelijking van die rode stippellijn!

1. Geef vergelijkingen van de scheve asymptoten van de grafieken van de volgende functies:

f(x) = 4 + ⁶/_x - 5x

f(x) = 3 + 2^-^x - 4x

y = 4 - 5x

y = 3 - 4x

y = 6 + 2x - ⁴/_{(x
- 5)}

f(x) = 4 + 5 • 3^x - x

y = 6 + 2x

y = 4 - x

y = 5 + x - ^6x/_x2

y = 5 + x

y = -2 - 3x

f(x) = 5 + ¹⁰⁰/_{(x +
1)} + ²⁰⁰/_{(x + 2)} + 2x

y = 5 + 2x

y = 4 + 4x

Maar helaas is het wiskundeleven niet altijd zo eenvoudig!
Vaak kun je aan een functievoorschrift niet meteen zulke stukken die te verwaarlozen zijn onderscheiden, maar moet je eerst wat algebrawerk verrichten voordat ze tevoorschijn komen. De volgende voorbeelden zullen dat hopelijk duidelijk maken.

DRIE TRUCS:

truc 1.

En aan deze laatste vorm kun je zien dat ³/_2x te verwaarlozen wordt voor grote x dus de scheve asymptoot zal de lijn y = 4x - 3 zijn.

truc 2.

En nu is te zien dat dit voor grote x gelijk zal zijn aan y = x + 2 omdat ⁵/_{(x
- 5)} te verwaarlozen wordt.

truc 3.
(een moeilijke!)

En onder die laatste wortel blijft alleen (x + 2)² over (de 2¹/₂ wordt voor grote x te verwaarlozen)
Nu geldt √((x + 2)² ) = ±(x + 2) (het plusteken voor x naar +∞ en het minteken voor x naar -∞)
Dus er staat y = ± 2(x + 2)
Voor positieve x zal de scheve asymptoot de lijn y = 2x + 4 zijn en voor negatieve x
de lijn y = -2x - 4
Meer hierover kun je lezen in de les over kwadraat afsplitsen.

Oké dan.... Tijd voor een blunder!

Ik had bovenstaande truc 3 voor scheve asymptoten geschreven en bedacht als voorbeeld de volgende mooie scheve asymptoot:

Mijn geweldig subtiele redenering ging als volgt (we bekijken positieve x-waarden):

En nu redeneerde ik als volgt: als x naar oneindig gaat, dan gaat ⁶/_x naar nul, dus gaat 9 + ⁶/_x naar 9 en die wortel dus naar 3. Dus staat daar, voor x naar oneindig, ongeveer y = 3 • x en dat is dan de scheve asymptoot.

Nou mooi.... Ik leunde tevreden achterover......Geen speld tussen te krijgen.....Ik was er eigenlijk wel trots op....
Zonder door te hebben dat ik nu een enorme BLUNDER had gemaakt!!!!
Zie jij het???

Ik zag mijn gruwelijke fout pas na een mailtje van Hans Walters uit Molenhoek.
Die deed het als volgt:

Nu kun je die 1 verwaarlozen, en komt er y = 3(x + ¹/₃) = 3x + 1 als scheve asymptoot uit!!!
Helaas, de GR gaf Hans gelijk:

Tja, dat is toch echt y = 3x + 1 en niet y = 3x.

Wat deed ik fout?

Nou kijk..... die ⁶/_x gaat inderdaad naar nul als x oneindig groot wordt, dat klopt wel.
En die 9 + ⁶/_x gaat inderdaad ook naar 9, dat klopt ook wel.
En die √(9 + ⁶/_x) gaat inderdaad ook naar 3.....
Maar als die wortel naar 3 gaat, dan betekent dat eigenlijk dat het verschil tussen die wortel en het getal 3 naar nul gaat.
Maar nou komt het: dat verschil wordt vermenigvuldigd met x. En die x gaat nou juist naar oneindig!!
En tja, als je iets dat naar nul gaat vermenigvuldigt met iets dat naar oneindig gaat, dan kun je niet zeggen wat daar uitkomt.

Neem bijvoorbeeld x = 1000. Dan is √(9 + ⁶/_x) = 3.000999833....
Maar 1000 • 3,000999833 = 0,999833... en dat gaat toch echt naar 1 toe!!
De moraal:

Pas op dat je niet "nul" met "oneindig" vermenigvuldigt!!

2. Geef vergelijkingen van de scheve asymptoten van de grafieken van de volgende functies:

y = 5x + 3

y = x - 1

y = x + 3

geen

y = 2 ± x√2

y = 3x + 4

y = (1±√3)x + 5

y = 2x + ¹/₃

y = x + 4

y = 6x + 4

De salarisschalen bij een bedrijf zijn zo gemaakt dat een beginnende werknemer snel in salaris stijgt. Die stijging wordt elk jaar minder groot. Uiteindelijk zal het salaris elk jaar met ongeveer een constant bedrag toenemen.

Men hanteert het salarismodel:

Daarbij is n het aantal dienstjaren en S het salaris. Een grafiek van S(n) staat hiernaast gegeven. In deze grafiek en de rest van de opgave mag je doen alsof het salaris continu toeneemt.

Wat is het aanvangsalaris bij dit bedrijf?

1200

De scheve asymptoot van de grafiek van S(n) is de lijn S = 800n + 2400

Toon dat algebraïsch aan.

Leg uit hoe je aan die scheve asymptoot kunt zien met welk constant bedrag het salaris uiteindelijk zal gaan toenemen.

Jolein gaat bij dit bedrijf werken dus voor haar salaris geldt de formule hierboven. Haar vriendin Carmen gaat tegelijkertijd bij een ander bedrijf werken. Dat andere bedrijf geeft een aanvangssalaris van €6000,- en verder een jaarlijkse opslag van €600,-

Bereken wanneer Jolein en Carmen het zelfde salaris zullen hebben

n = 18,3

Benader het moment waarop Jolein en Carmen het zelfde salaris zullen hebben met behulp van de scheve asymptoot van S(n) en vergelijk je antwoord met het antwoord op vraag d).

n = 18

Gegeven is de familie van functies:

Voor welke twee waarden van p is de grafiek een rechte lijn?

0 en 4

Geef de vergelijking van de scheve asymptoot van f₃.

y = x + 1

Voor welke p is de lijn y = x + 6 scheve asymptoot van de grafiek van f_p?

p = -2

Examenvraagstuk VWO wiskunde B, 2021-II

Voor p > 0 wordt de functie f_p gegeven door: f_p(x) = ^{(x³ + 4p)}/_x²
In de figuur is de grafiek van f₁ weergegeven.

De grafiek van f₁ heeft een scheve asymptoot.
Bewijs dat de grafiek van f₁ boven deze scheve asymptoot ligt.

Examenvraagstuk VWO Wiskunde B, 2022-I

De functie f is gegeven door f (x) = x + ²/_x.

De grafiek van f heeft een verticale asymptoot met vergelijking x = 0 en een scheve asymptoot. In de figuur hiernaast is voor x > 0 de grafiek van f weergegeven. De scheve asymptoot is gestippeld weergegeven.

Op de grafiek van f ligt een willekeurig punt P (p, p + ²/_p).

De raaklijn aan de grafiek van f in P snijdt de verticale asymptoot in punt Q en de scheve asymptoot in punt R. Zie de figuur.

Bewijs dat P het midden is van lijnstuk QR.

Examenopgave VWO Wiskunde B 2023-I.

De functie f wordt voor x > 0 gegeven door f(x) = 2x + ¹/_x
Lijn k is de scheve asymptoot van de grafiek van f.
Het vlakdeel V wordt ingesloten door de grafiek van f, lijn k en de lijnen met vergelijking
x = a en x = 2a met a > 0 . In de figuur is dit vlakdeel voor een zekere waarde van a geel gemaakt.

De oppervlakte van dit vlakdeel is onafhankelijk van de waarde van a.
Bewijs dit.