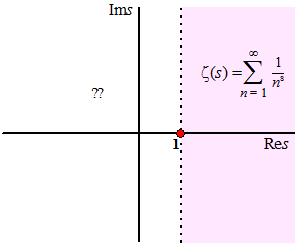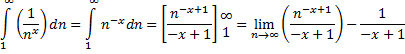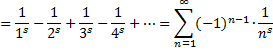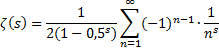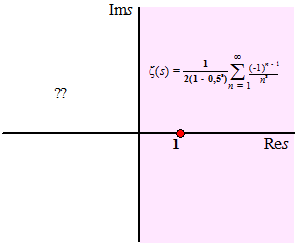Riemann zetafunctie


	© h.hofstede (h.hofstede@hogeland.nl)

De Riemann Zetafunctie

Bernhard Riemann was een vrij slimme dude, en dacht: waarom zou ik die zetafunctie niet ook voor complexe getallen kunnen gebruiken?

Tja, waarom eigenlijk niet.....???

Je kunt elke functie (die een beetje "normaal" is) die je op een deel van het complexe vlak kent namelijk uitbreiden naar het hele complexe vlak, en dat kan maar op één unieke manier. Dat heet de analytische voortzetting van zo'n functie en waarom dat kan en waarom dat zo is dat wordt in deze les behandeld.

De "gewone" definitie van ζ(s) = ∑¹/_ns werkt alleen voor complexe getallen waarvoor Res > 1.
Als dat namelijk niet zo is, dan is |n^s| te klein en dan divergeert de reeks.
Dat kun je zó zien (stel het complexe getal s = x + iy):

(de modulus van eⁱ^j is immers 1)
Dat betekent dat je alleen naar het reële deel van s hoeft te kijken. In de les over de integraaltest kun je zien dat je het convergeren/divergeren van een reeks kunt vergelijken met dat van de bijbehorende integraal (een integraal is immers ook een soort som).

(denk erom dat n de integratievariabele is!).
Die limiet convergeert als x > 1, want dan is de macht van n negatief. Dus ζ(s) convergeert voor Res > 1
Voor s = 1 heeft de functie een singulier punt, immers we zagen in een eerdere les al dat ζ(1) = ∞. Ook hier zie je dat x = 1 niet is toegestaan.

Laten we proberen deze functie uit te breiden naar de rest van het complexe vlak.

1. Uitbreiding naar Re(s) > 0

We gaan de gewone ζ(s) nu iets aanpassen met een trucje.
Bekijk de functie (1 - 2 • 0,5^s) • ζ(s) en je ziet iets leuks gebeuren:

Breng nu de factor (1 - 2 • 0,5^s) naar de andere kant en je hebt een andere definitie van ζ(s):

Dat stuk daar onder dat somteken heet ook wel de h-functie
Dat is een rij die convergeert voor Re(s) > 0 (behalve in s = 1 want dan wordt de noemer van die breuk nul).

Waarom convergeert die rij?
In deze les over alternerende rijen kun je zien dat een alternerende rij die monotoon afneemt altijd convergeert.

Nou, dit is er voor Re(s) > 0 zo eentje dus die convergeert....

Oké, de rij convergeert dus, en omdat die rij voor Re(s) > 1 hetzelfde is als de oude ζ(s) moet het wel de analytische voortzetting ervan zijn. Die is immers uniek.

2. Uitbreiding naar Re(s) < 0

Dat is een stukje lastiger, hier begint het eigenlijke werk van Bernhard Riemann.

Riemann publiceerde in 1859 zijn enige werk over de getaltheorie, getiteld "Uber die Anzahle der Primzahlen unter einen gegebenen Grosse". Het was dan wel zijn enige werk op dit gebied maar het was meteen een knaller en werd één van de invloedrijkste werken uit de getaltheorie
Riemann ontdekte een methode om een verband tussen ζ(s) en ζ(1 - s) te vinden.
Daarvoor had hij een zogenaamde functionaalvergelijking van ζ(s) nodig.

De functionaalvergelijking die Riemann vond zag er zó uit:

De afleiding ervan is een boeiend stuk wiskunde. Het voert ons langs Complexe Fouriertransformatie, Poissonsommatie, Thetafunctie, Gammafunctie, Gauss-integraal.

Als je zin hebt in deze lange wiskundereis (zeg maar gerust expeditie) dan kun je die hiernaast beginnen.

Lang en uitputtend, maar uiteindelijk beslist de moeite waard!
't Is namelijk gewoon een stuk mooie wiskunde.....

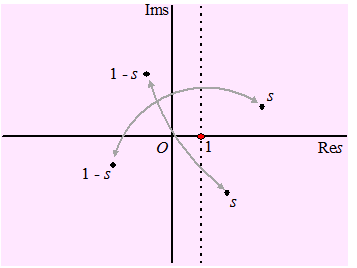
Omdat die functionaalvergelijking een verband tussen ζ(s) en ζ(1 - s) geeft, kun je nu ook de waarden voor ζ(s) in het complexe vlak voor Res < 0 vinden: je koppelt ze gewoon aan waarden in het al bekende deel, immers als je van s naar 1 - s gaat, dan spiegel je eigenlijk in het punt s = 1.

Daarmee is de zetafunctie overal op het complexe vlak gedefinieerd (behalve in s = 1 want we wisten al dat ζ(1) = ∞)