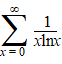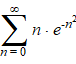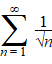integraaltest


De Integraaltest.	© h.hofstede (h.hofstede@hogeland.nl)

Bij rijen is het altijd erg belangrijk of ze convergeren of divergeren. Bij het bestuderen van webgrafieken hebben we het daar al over gehad. Het komt er kortweg op neer dat van rijen die convergeren de som steeds dichter bij een bepaalde grenswaarde komt te liggen. Door meer en meer termen van de rij te nemen kun je ervoor zorgen dat de som willekeurig dicht bij die grenswaarde komt.
Als een rij niet convergeert, dan divergeert hij. Dat kan bijvoorbeeld doordat de som oneindig groot wordt, maar ook omdat de som "heen en weer blijft springen" en niet naar een bepaalde grenswaarde toeloopt.

Om te testen of een rij convergeert of divergeert kun je soms handig gebruik maken van integralen.

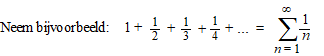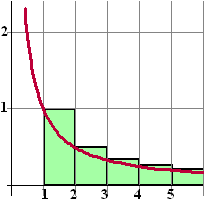
Daar kun je de figuur hiernaast bij bedenken. Die groene blokjes hebben precies de oppervlaktes van de termen uit de rij.
Vergelijk de oppervlaktes van die blokjes met de oppervlakte onder de grafiek van y = ¹/_x die er rood bijgetekend is. Dan zie je dat de oppervlakte van die blokjes samen meer is dan de oppervlakte onder de grafiek (er steken steeds stukjes bovenuit). Maar de oppervlakte onder de grafiek is een integraal:

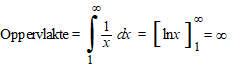Als de oppervlakte onder de grafiek oneindig groot wordt, en die blokjes hebben een grotere oppervlakte, dan moet de oppervlakte van al die blokjes samen dus ook wel oneindig groot worden.
Kortom: de rij divergeert!

Andersom kan natuurlijk ook.

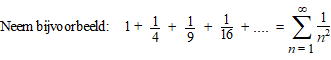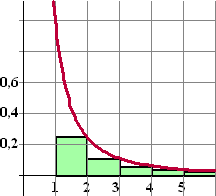
Hiernaast zie je weer zulke groene blokjes, deze keer bij de grafiek van y = ¹/_x2.
Nu zie je dat de oppervlakte van de groene blokjes kleiner is dan de oppervlakte onder de grafiek. Die oppervlakte onder de grafiek is gelijk aan:

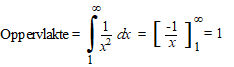De oppervlakte van al die groene blokjes samen blijft kleiner dan 1. Die groene blokjes zijn de getallen ¹/₄ + ¹/₉ + ¹/₁₆ + ... dus de rij zelf is nog 1 groter (de eerste term van de rij staat niet bij de blokjes).

We hebben dus te maken met een rij die steeds groter wordt (alle termen zijn positief) maar altijd onder de 2 blijft. De rij is daarom convergent. Denk erom: we weten nu nog niet naar welke grenswaarde de rij loopt, alleen dat die kleiner of gelijk aan 2 is (Voor wie nieuwsgierig is: de precieze waarde is trouwens ^π²/₆ = 1,64....).

Oké, en nu wat wiskundig verantwoorder:

Het integraalcriterium van Cauchy.

Dit is gewoon een wat nettere manier om bovenstaand verhaal weer te geven.
Stel je hebt een reeks Σa_n met alle termen positief (a_n > 0).
Stel verder dat er een reële functie f bestaat zodat f continu en dalend is vanaf bepaald interval [p, →〉
en waarvoor geldt f(n) = a_n.

Dan geldt:

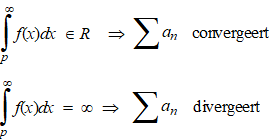Laten we voor de verandering eens een lekker officieel bewijs bekijken. Gewoon de mouwen opstropen en lekker wiskunde bedrijven!

Bewijs.

Neem een geheel getal k > p.
Omdat f dalend is op interval [k, k + 1] geldt voor elke x uit dit interval dat f(k + 1) ≤ f(x) ≤ f(k)
Dus dat betekent dat a_k_{+ 1} ≤ f(x) ≤ a_k

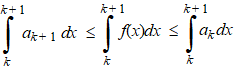Maar die eerste en laatste integralen zijn van constante getallen (a_k en a_k_{+ 1}) , dus kun je de integralen berekenen:

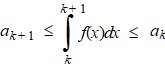
Schrijf dit nu op voor a_{p+
1}, a_p_{+ 2}, .... , a_n   en tel die allemaal bij elkaar op:
a_p_{+ 1} + a_p_{+ 2} + ... + a_n_{+ 1}   ≤ a_p + a_p_{+ 1} + ... + a_n
Maar daar staan de deelsommen S van de rij a_n.
Dus daar staat gewoon S_{n + 1} - S_p ≤ S_n - S_{p - 1}

Nu laten we n naar oneindig naderen:

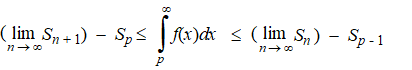Als die middelste integraal nou een reëel getal is, dan is die linkerkant ook een reëel getal, dus is die eerste limiet ook reëel (immers S_p is een eindig getal). Maar als lim S_{n + 1} een reëel getal is, dan convergeert de rij a_n.

En op dezelfde manier: als die integraal oneindig is, dan is ook de rechterkant oneindig, dus is ook lim S_n oneindig dus divergeert de rij a_n.

OPGAVEN

Bepaal of de volgende rijen convergeren of divergeren.

divergent

convergent

divergent

De reeks van Dirichlet (of ook wel de hyperharmonische reeks) is de reeks

Toon aan dat de reeks convergeert als p > 1 en divergeert als 0 < p ≤ 1.