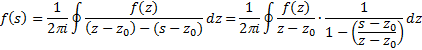© h.hofstede (h.hofstede@hogeland.nl)

Reeksontwikkelingen.
       
Bij "gewone" reële functies kun je zo'n functie meestal schrijven als een reeksontwikkeling, en daarmee krijg je vaak een aardig idee van hoe zo'n functie zich gedraagt. Dat staat in deze les over Taylorreeksen, en de conclusie daar was:
       

       
Hier zijn een paar beroemde voorbeeldjes (steeds een reeksontwikkeling rond x = 0):
       
•

•

•

       
Best handig:  zo kun je bijvoorbeeld aan de tweede reeks zien dat in de buurt van 0  sinx/x gelijk wordt aan 1, en aan de eerste reeks dat de afgeleide van ex weer gelijk is aan ex , en nog veel meer van zulk soort nuttige eigenschappen.

De convergentiestraal van zo'n reeks geeft aan hoe ver je van a af mag zitten zodat de reeks nog convergeert.
Dus  r =  | x - a |
 
Wauw! Handig!!  Kan dat ook voor een complexe functie?
       
Jazeker.
Met behulp van de stelling van Cauchy kun je een reeksontwikkeling voor een complexe functie maken. Kijk, als je de stelling van Cauchy namelijk gewoon wat anders noteert dan staat er dit:
       

       
Daar staat dus eigenlijk de functiewaarde f(s) in een punt, maar dan berekend met behulp van een integraal rondom s. Daar kun je op een nogal gekunstelde manier een machtreeks van maken, kijk maar:
       

z0 is  de waarde waaromheen we de reeksontwikkeling gaan opstellen  (de a van de Taylorreeks hierboven).
Die laatste breuk daar rechts is van de vorm  1/1-x  en dat is precies de som van de meetkundige rij 1 + x + x2 + ....  Zie het derde voorbeeld bij de Taylorreeks hierboven. Dat betekent dat je dit ook zó kunt schrijven:
       

Die s - z0  hangt niet van z af dus die kon buiten de integraal.
Dit was eigenlijk gewoon een trucje om  (s - z0)n apart te krijgen, zodat het een Taylorreeks wordt.
Als je nou dat stuk daar tussen die vierkante haken ziet als  an, dan staat er namelijk een mooie reeksontwikkeling voor f(s) rondom z = z0:  
       

       
Hier hebben we de complexe variant van de Taylorreeks. Die coëfficiënt an  is trouwens hetzelfde als  de 1/n! • f(n)(s)  van de reële Taylorreeks.
       
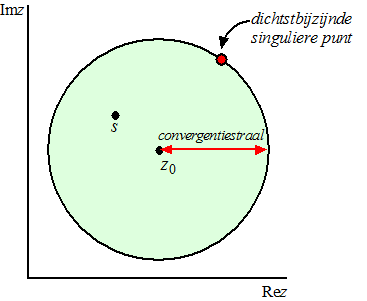
Ik heb het expres de hele tijd niet over de convergentiestraal van de reeksen gehad. Hoogste tijd om dat gebrek te herstellen.

Kijk, hierboven staat een reeksontwikkeling rondom het punt  z0  waarmee je f(s) kunt benaderen. Maar dan moet die f(z) in die integraal zich wel een beetje normaal gedragen.

Dat is zo, als je maar niet te ver van z0 afkomt.  Er mogen geen singuliere punten van  f(z) binnen de integraal liggen!

Kortom:  de reeksontwikkeling geldt zolang je s maar binnen dat groene cirkeltje hiernaast kiest.
(Dat cirkeltje heet dan ook de convergentiecirkel)
       
Analytische voortzetting.
       
En hoe is het met punten buiten de convergentiecirkel?
Om die ook te kunnen bereiken hebben we een belangrijke stelling nodig:
       

Als twee analytische functies  f en g op een klein gebied of een deel van een curve helemaal gelijk zijn,
dan zijn ze overal op hun hele domein gelijk.
       
Om dat te bewijzen moeten we eerst een kleine hulpstelling aantonen, en dat is de volgende:
       

De nulpunten van een analytische functie zijn geïsoleerde punten.
       
Dat betekent dat een analytische functie  f  niet overal op een curve of gebied nul kan zijn.  (Als enige flauwe uitzondering is er natuurlijk de constante functie f = 0). Dat dat inderdaad zo is kun je makkelijk zien door de reeksontwikkeling van f  in een nulpunt te bekijken.
Als dat nulpunt  z0 is, dan is de reeksontwikkeling in de buurt van z0:  
f(z) = a0(z - z0)0 + a1(z - z0)1 +  a2(z - z0)2 + .....
f(z) = a0 +  a1(z - z0) +  a2(z - z0)2 +  .......  
Maar dan is in ieder geval a0 = 0, want als je z = z0 kiest dan moet er nul uitkomen.
Van de rest van de a's kun je nog niet veel zeggen........
Stel dat aN de eerste a is die NIET gelijk is aan nul  (dat kan dus al a1 zijn). Dan is de reeksontwikkeling zó te schrijven:
f(z) =  aN(z - z0)N  + aN+1 • (z - z0)N + 1 +  aN+2 • (z - z0)N + 2 + .....   en laten we nu (z - z0)N buiten haakjes halen: 
f(z) = (z - z0)N •  { aN + aN + 1 • (z - z0) + aN + 2 • (z - z0)2  + ...... }
Daar tussen die accolades staat nu weer een machtsreeks van een functie die overal analytisch is, en bovendien in z = z0  niet gelijk aan nul. Maar omdat die functie continu is bestaat er dus een omgeving van z0  waarin die functie overal verschillend van nul is.
Dus was dat nulpunt van f een geïsoleerd nulpunt.
Daarmee is de hulpstelling bewezen.

Neem nu twee analytische functies f en g  en kijk naar het verschil  f - g
Dat verschil is weer een analytische functie dus heeft volgens bovenstaande stelling geïsoleerde nulpunten.
Maar die nulpunten zijn precies de punten waarin f = g
Dat betekent dus dat de punten waar geldt f  = g  óók geïsoleerde punten zijn. Dus kunnen f en g niet over een heel gebied of een hele curve overal gelijk zijn.
Dat kan alleen als  f = g  (dan is de verschilfunctie overal nul).
       

       
Dat betekent bijvoorbeeld ook dat je een reële functie (die dus gedefinieerd is op de reële as)  maar op één manier analytisch kunt uitbreiden naar het hele complexe vlak.
Maar dat betekent ook dat je met reeksontwikkelingen ook punten kunt bereiken die buiten de convergentiestraal van de reeks liggen. 
Dat gaat zó:
       

       
Stel dat je een reeksontwikkeling hebt gemaakt rond een punt z0 waarvan s het dichtstbijzijnde singuliere punt is, zoals in de figuur links. Dan kun je die niet gebruiken om de waarde in z uit te rekenen want z ligt buiten de convergentiecirkel.
Maar punt z1 kun je wel bereiken want dat ligt er binnen. Als je de hele reeksontwikkeling in z1 weet, dan kun je een nieuwe reeksontwikkeling rondom z1 maken, en daarmee kun je z wél bereiken, want daarvoor geldt de blauwe convergentiecirkel in de figuur rechts.

Voorbeeldje
 
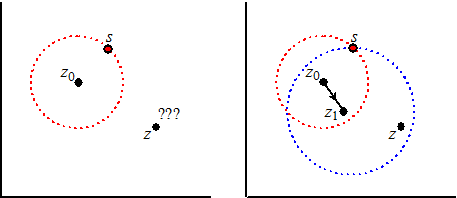
Neem de eenvoudige reeksontwikkeling  voor
f(z) = 1/(1 - z)vanuit  z0 = 0.
Die is  f(z) = z + z2 + z3 + z4 + ...  met convergentiestraal 1.
Als je de waarde in z = 11/2i wilt schatten dan mag je dus deze reeksontwikkeling niet gebruiken want dat punt ligt buiten de rode cirkel hiernaast. Doe het stiekem tóch  maar eens:  met z = 11/2i  divergeert de reeks, terwijl we toch weten dat er  1/(1 - 1½i) = 4/13 + 6/13i  moet uitkomen!!

De reeksontwikkeling vanuit  z = 1/2i  mag wél en die moet precies dezelfde functie weergeven als die vanuit z0, immers op een gebied zijn beiden gelijk.

Vanuit z = 1/2i is de reeksontwikkeling:

Al die afgeleides met die faculteiten erbij geven steeds  f(n) (1/2i) • 1/n! =   1/(1 - ½i)n+1 dus dan wordt de reeks:

En nu kun mag je wél z = 11/2i invullen omdat dat punt binnen de blauwe convergentiecirkel hierboven ligt.

Deze reeks convergeert netjes naar  4/13 + 6/13i .  Ga dat maar na door een stuk ervan uit te rekenen, of lees het bewijsje hiernaast.
     
Zo kun je voor functies met allemaal singulariteiten s  toch elk punt bereiken, met een serie overlappende convergentiecirkels.  Dat ziet er ongeveer zó uit:
       

       
Vanaf punt z0 links kun je zo via een serie overlappende cirkels punt z rechts "bereiken". Zo vind je een Taylorreeks voor z die dezelfde functie voorstelt als de Taylorreeks rond z0.  Dat is natuurlijk ontzettend veel werk en erg onhandig, maar het gaat hier eigenlijk vooral om het principe: 
       
       

© h.hofstede (h.hofstede@hogeland.nl)