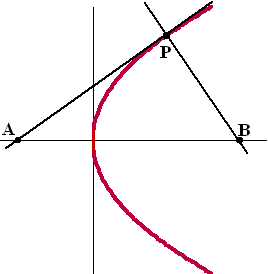raaklijnen parabool

© h.hofstede (h.hofstede@hogeland.nl)

Raaklijnen aan een parabool.

De handigste manier om de helling van een punt van een willekeurige parabool te bepalen is door middel van impliciet differentiëren. Als je niet meer weet hoe dat ook al weer ging moet je eerst deze les doornemen.
Voor parabolen geeft dat:

y² = 4cx ⇒ 2y • y' = 4c ⇒ y' = ^2c/_y
x² = 4cy ⇒ 2x = 4c • y' ⇒ y' = ^x/_2c

Daarmee kun je de helling (a) van de raaklijn bepalen, en daarna vind je het snijpunt met de y-as (b) door het raakpunt in te vullen. Makkie. Vaak genoeg gedaan, dacht ik.

Ook bij parabolen met translaties geeft dat niet echt onoverkomelijke problemen. Kijk maar:

Voorbeeld.
Gegeven is de parabool y² + 4y - 2x - 5 = 0. Geef de vergelijking van de raaklijnen bij x = 8.

Oplossing:
2y • y' + 4y' - 2 = 0
y' • (2y + 4) = 2
y' = ²/_{(2y + 4)}
x = 8 geeft y² + 4y - 21 = 0 ofwel y = 3 ∨ y = -7
y = 3 geeft helling y' = 0,2 dus y = 0,2x + b en het punt (8,3) geeft dan b = 1,4 dus is de raaklijn y = 0,2x + 1,4
y = -7 geeft helling y' = -0,2 dus y = -0,2x + b en het punt (8, -7) geeft dan b = -5,4 dus is de raaklijn y = -0,2x - 5,4

Loodrecht snijden.

Als je een raaklijn aan een parabool kunt opstellen, dan kun je natuurlijk ook een lijn opstellen die de parabool loodrecht snijdt. Dat is de lijn die loodrecht op de raaklijn staat.
Weet je het nog? Hoe zat dat ook alweer met lijnen die loodrecht op elkaar staan?

loodrechte stand: a₁ • a₂ = -1

De tweede raaklijn in het voorbeeld hierboven was de lijn y = -0,2x - 5,4
De lijn daar loodrecht op zal helling a = 5 hebben (want 5 • -0,2 = -1) dus het zal de lijn y = 5x + b zijn.
Omdat hij ook door (8,-7) moet gaan geldt -7 = 5 • 8 + b ofwel b = -47
Het is dus de lijn y = 5x - 47

Discriminant-Methode.

• Als een lijn een parabool raakt, dan betekent dat, dat hij maar één punt gemeenschappelijk met de parabool heeft.
• Dat betekent dus, dat je maar één oplossing mag vinden als je het snijpunt van lijn en parabool wilt gaan berekenen.
• Zo'n snijpunt-berekening geeft altijd een kwadratische vergelijking.
• Deze kwadratische vergelijking mag dus maar één oplossing hebben
• Dat is zo als de discriminant gelijk is aan nul!

Deze vijf stappen geven een andere manier om een raaklijn te bepalen.
Snij de parabool y² = 4cx met de lijn y = ax + b
Dat geeft   (ax + b)²= 4cx ⇒ a²x² + 2abx + b² - 4cx = 0   ⇒ a²x² + x(2ab - 4c) + b² = 0
Stel de discriminant gelijk aan nul: (2ab - 4c)² - 4a²b² = 0
Dat geeft 4a²b² - 16abc + 16c² - 4a²b² = 0 ⇒   ab = c
Een mooi eenvoudig resultaat!

Voorbeeld 2.

De lijn y = 2x + b   raakt de parabool y² = 12x. Bereken b.

Oplossing:
y² = 12x betekent dat c = 3. omdat a = 2 geldt dan b = ^c/_a = 1¹/₂. het is dus de lijn y = 2x + 1¹/₂.

Deze methode geeft in sommige gevallen (zoals hier) supersnel een oplossing, maar lang niet altijd. De eerste manier hierboven is veel algemener natuurlijk.

Opmerking:
Als de parabool de top niet in de oorsprong heeft, schuif hem dan eerst daarheen, bepaal de raaklijn op de manier hierboven, en schuif die raaklijn tenslotte weer terug.

Er is een nog mooiere manier om raaklijnen op te stellen, en dat gaat via zogenaamde poollijnen. Hoe dat werkt zullen we in een latere les zien.

3. Grappige Raaklijneigenschap.

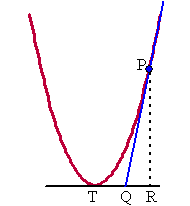
Raaklijnen aan een parabool hebben een grappige eigenschap. Zie de figuur hiernaast. Een raaklijn in een punt P snijdt de horizontale lijn door de top in punt Q, en daarbij geldt: Q ligt midden tussen T en R in!!! (R is de projectie van P op de lijn door de top)

TQ = QR

En die eigenschap geldt natuurlijk ook als de figuur 90º gedraaid wordt. Omdat je meestal snel punt Q en P kunt vinden kun je daarmee makkelijk een vergelijking van PQ opstellen.

Geef in de volgende gevallen een vergelijking van de raaklijn:

Parabool y² - 2y - 6x - 23 = 0 in het punt waar y = 7.

y = ¹/₂x + 6

Parabool 2y² + 16x - 32 = 0 in het punt waar y = 8.

y = -¹/₂x + 5

Parabool -3y² - 18y - 2x - 17 = 0 in het punt waar y = 1.

y = -¹/₁₂x - ⁷/₁₂

Welk resultaat geeft de discriminant-methode als een lijn y = ax + b een parabool van de vorm x² = 4cy moet raken?

a²c + b = 0

De lijn met vergelijking y = 2x + b snijdt de parabool y² = -8x loodrecht.
Bereken b.

b = 24

De lijn met vergelijking y = 0,4x + b is een raaklijn van de parabool y² + 2y = 4x + 12
Bereken b.

b = 2,8

De lijn y = -0,8x + 4 raakt de parabool y² = ax
Bereken a.

a = -12,8

Gegeven is de parabool y² = 10x.

P is het punt (2¹/₂, 5) en ligt op de parabool.
De raaklijn aan de parabool in punt P snijdt de x-as in punt A.
De lijn die de parabool loodrecht in P snijdt, snijdt de x-as in punt B.
Zie de figuur hiernaast.

Bereken de afstand AB.

AB = 10

Iemand beweert dat x_B = 5 + x_P en dat lijkt voor bovenstaand geval te kloppen.

Toon aan dat dit verband inderdaad voor alle punten op de parabool geldt.

De parabolen y² = 32x en y² + 8x - 80 = 0 snijden elkaar loodrecht. Toon dat aan.

Gegeven is de parabool y² = 6x - 15

Bereken de snijpunten van de lijn y = x - 7 met de parabool

(16,9) en (4,-3)

Voor welke a raakt de lijn y = ax deze parabool?

a = ±√(0,6)