Raaklijnen aan cirkels.

© h.hofstede (h.hofstede@hogeland.nl)
   
Hiernaast zie je een cirkel met middelpunt M.
In een willekeurig punt R van de cirkel is een raaklijn aan de cirkel getekend.
(een raaklijn is een lijn die precies één punt met de cirkel gemeenschappelijk heeft).
Nu geldt de volgende eigenschap:
 

de straal MR staat loodrecht op de raaklijn in R
 

Ik hoop dat je dat uit het plaatje direct heel logisch vindt.
De cirkel is immers symmetrisch ten opzichte van MR, dus moeten die beide hoeken bij R wel aan elkaar gelijk zijn, dus 90º.
Stel bijvoorbeeld dat de linker hoek groter is dan de rechter. Als je de cirkel dan van de achterkant bekijkt zie je precies dezelfde figuur maar dan is ineens de rechter hoek groter. Dat kan niet!
 
Euclides kwam er pas aan toe in propositie 16 van boek III.
Zijn bewijs staat hiernaast.
   
Tussendoortje:  De constructie van een raaklijn aan een cirkel.
   
Je kunt die rechte hoek samen met de stelling van Thales  goed gebruiken om een raaklijn aan een cirkel vanuit een punt P erbuiten te construeren.
Noem S het midden van MP.
Teken een cirkel met middelpunt S en straal PS.
Die snijdt de eerste cirkel in het raakpunt R.
Immers, omdat P op de tweede cirkel ligt, en omdat MP daar een middellijn van is, zal hoek PRM gelijk zijn aan 90º, dus staat PR loodrecht op MR, dus is PR de raaklijn in R.

   
Hoek tussen koorde en raaklijn.
   
Die 90º tussen straal en raaklijn heeft een belangrijk gevolg.
Kies een willekeurig punt P van de cirkel en teken koorde PR.
Teken ook de middellijn PT.

Nu geldt:
∠QRP + ∠PRM = 90º  (raaklijneigenschap hierboven)
∠PRM + ∠MRT = 90º  (stelling van Thales)

Dus is ∠QRP = ∠MRT  (1)
 
Maar  omdat MR = MT (straal van de cirkel) is driehoek MRT gelijkbenig, dus geldt ∠MRT = ∠MTR  (2)

Uit (1) en (2) volgt   ∠QRP = ∠PTR.

Conclusie:  
 

De hoek tussen een raaklijn en een koorde is gelijk aan de omtrekshoek van die koorde
   
   
OPGAVEN
   
1. Examenvraagstuk Wiskunde B, 2011.

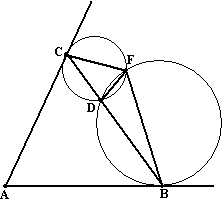
 D is een willekeurig punt op zijde BC van driehoek ABC.
De cirkel door D die AB raakt in B en de cirkel door D die AC raakt in C hebben koorde DF gemeenschappelijk.

Bewijs dat vierhoek ABFC een koordenvierhoek is.

       
2. Stelling:
"Als de raaklijn in R aan een cirkel evenwijdig is aan koorde PQ, dan is driehoek PQR gelijkbenig".

Bewijs deze stelling.
       
3. De machtsstelling:

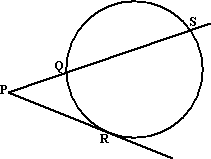
Voor een willekeurige lijn door een punt P buiten een cirkel die de cirkel in Q en S snijdt,  en een raaklijn PR geldt   
PQ • PS = PR2 

Bewijs deze stelling.

       
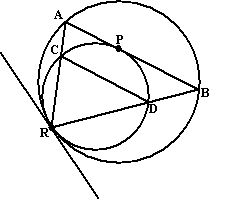
4. Twee cirkels raken elkaar in R.
Een raaklijn aan een willekeurig punt P van de kleinste cirkel snijdt de grootste in A en in B.
RA en RB snijden de kleinste cirkel in C en D.

Toon aan dat DC evenwijdig is aan AB.
 

       
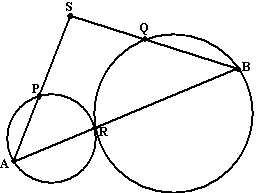
5. Twee cirkels raken elkaar in R.

Een lijn door R snijdt de cirkels in A en in B.
S is een willekeurig punt buiten de cirkels.

SA en SB snijden de cirkels in P en Q.

Toon aan dat P, Q, R en S op één cirkel liggen.

       
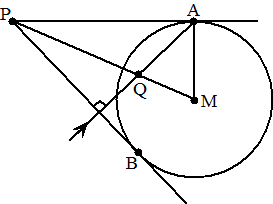
6. PA en PB zijn twee raaklijnen aan een cirkel.
AQ staat loodrecht op PB en snijdt PM in Q.

Toon aan dat AQ = AM

     
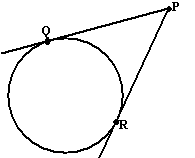
7. Vanuit punt P buiten een cirkel worden twee raaklijnen PQ en PR aan de cirkel getekend.

Toon aan dat PQ = PR.

       
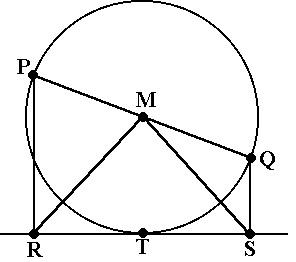
8. PMQ is middellijn van een cirkel met middelpunt M.
RS is de raaklijn aan de cirkel in T.
PR en QS staan loodrecht op RS.

Bewijs dat MR = MS

 

       
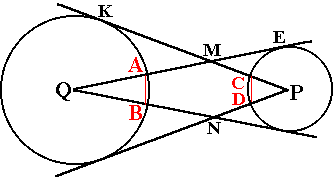
9. Teken van twee niet-snijdende cirkels de raaklijnen van een middelpunt van de ene cirkel aan de andere cirkel.

Bewijs dat AB = CD
     
 
hint: QKM ~  PEM en   QAB ~ QMN
       
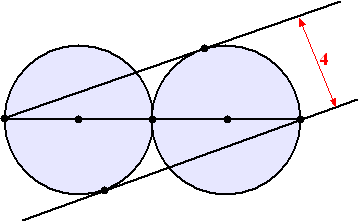
10. Olympiadevraagstuk.

Twee  even grote cirkels raken elkaar. 
De lijn door het raakpunt en beide middelpunten snijdt de cirkels in P en Q.
Teken de raaklijnen vanuit P en Q aan de andere cirkel zoals hiernaast is gedaan. 

De afstand tussen deze twee raaklijnen blijkt gelijk te zijn aan 4.
Bereken de straal van de cirkels.
     

r = 3
       
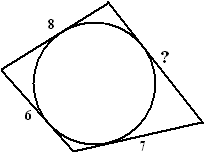
11. Olympiadevraagstuk.

Een cirkel past precies in een vierhoek (alle vier de zijden raken aan de cirkel).
Drie zijden hebben lengtes 7, 6 en 8 zoals in de figuur.

Bereken de lengte van de vierde zijde.

 

     

 9

       
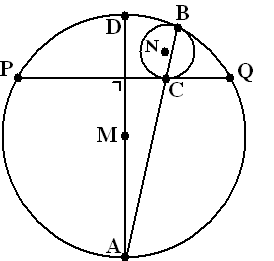
12. AD is de middellijn van een cirkel met middelpunt M.
PQ staat loodrecht op AD.
Er wordt een tweede cirkeltje getekend dat PQ raakt in C en de eerste cirkel in B.
Dat wordt zodanig gedaan dat BCA op één lijn liggen.
Het middelpunt van dit tweede cirkeltje is N.

Bewijs dat MN door B gaat.

 

       
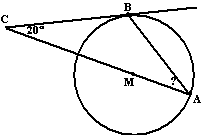
13. Vanuit punt A op de omtrek van een cirkel wordt een lijn door het middelpunt getrokken
Verder wordt een lijn naar een willekeurig ander punt B getrokken.
De raaklijn aan B aan de cirkel snijdt het verlengde van AM in punt C.
Het blijkt dat hoek BCA gelijk is aan 20°

Bereken hoek CAB.

     

 35º

       

© h.hofstede (h.hofstede@hogeland.nl)