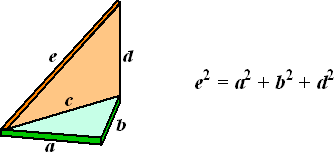Ruimtelijk Pythagoras.

© h.hofstede (h.hofstede@hogeland.nl)
   
Stel dat je de lengte van de lichaamsdiagonaal EC in de balk hiernaast wilt uitrekenen. Dan kun je dat als volgt doen.

Bekijk driehoek EAC. Die heeft een rechte hoek, namelijk bij A. Dus kun je in deze driehoek Pythagoras toepassen:  EC2 = EA2 + AC2 . Maar ja, AC weet je niet!

Wacht eens even.. AC kun je eerst berekenen met Pythagoras in driehoek ABC.  Dat geeft  AC2 = AB2 + BC2 = 42 + 62 = 52 dus  AC = √52

Nu terug naar de eerste Pythagoras:
EC2 = 32 + (√52)2 = 32 + 52 = 61   dus  EC = √61

 
Zie je wat er in die laatste regel eigenlijk staat?
Vervang die 52 weer door  42 + 62  want daar kwam hij vandaan.
Dan staat er  EC2 = 32 + 42 + 62  en dat zijn precies de drie zijden van de balk.
Dat werkt altijd zo bij balken: gewoon de drie zijden kwadrateren!
 
     
 
 
 

 
Je kunt dat ook makkelijk inzien met de figuur hiernaast. Daar staan twee rechthoekige driehoeken aan elkaar vast getekend.
In de groene driehoek geldt  c2 = a2 + b2
Daarna geldt in de oranje driehoek 
e2 = d2 + c2 = d2 + a2 + b2

Wat heeft dit met ruimtelijk Pythagoras te maken? Nou, zet een 3D-bril op, en draai de oranje driehoek gewoon rechtop:

   

 
Die zijde e is nu precies de schuine zijde door een balk met zijden a en b en d.
En je hoeft natuurlijk niet te gaan zitten wachten tot er precies zo'n diagonaal gevraagd wordt. Vaak kun je het heft in eigen handen nemen door zélf een balk te tekenen waarvan de gevraagde lengte zo'n diagonaal is.

Kijk maar naar deze voorbeelden:
   
Voorbeeld 1.

Als je PM in de kubus hiernaast moet berekenen, dan kun je er natuurlijk makkelijk zélf een balk in zetten waarvan PM de diagonaal is.
Dat is in de rechterfiguur gebeurd.

Daarin zie je nu eenvoudig dat PM2 = 32 + 42 + 62
Dus PM2 = 61  ofwel PM = √61.
   
Voorbeeld 2.

Als je in de piramide hiernaast de afstand MS moet berekenen kun je er zelf weer zo'n blauwe balk bij in denken.
Die heeft afmetingen 2 bij 2 bij 5 omdat M het midden van de ribbe is.

Dus MS2 = 22 + 22 + 52 = 33
MS = √33.

   
 
  OPGAVEN
 
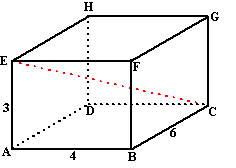
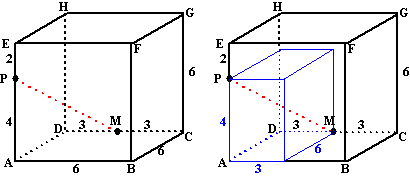
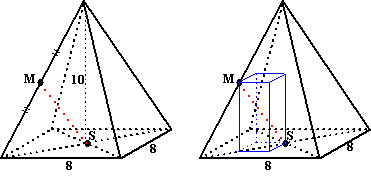
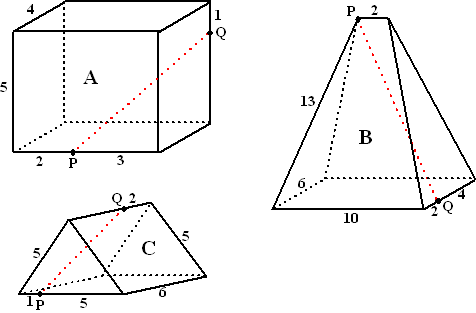
1. Bereken de lengte van PQ in de volgende ruimtelijke figuren (de figuren zijn allemaal symmetrisch).
       
 

     

A:√41;   B:√181 ;  C: 6
       
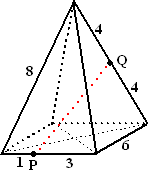
2. a. Bereken de hoogte van de piramide hiernaast

   

√51
  b. Bereken de afstand PQ in de piramide hiernaast.
   

√37
     
       
3. Een leuke stelling...

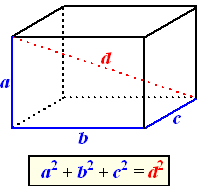
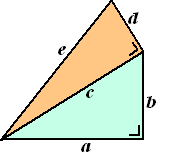
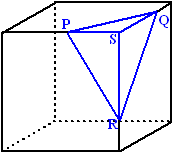
Als je een hoek van een kubus of balk afsnijdt, dan krijg je een viervlak zoals de blauwe figuur hiernaast. Daar is iets grappigs mee aan de hand. Het viervlak bestaat uit drie rechthoekige driehoeken (PQS en PRS en QRS) en één andere driehoek (PQR). Nu blijkt de volgende stelling te gelden:
 
(opp. PQR)2 = (opp. PSR)2 + (opp. QSR)2 + (opp. PQS)2
 

Hilarisch toch? Daar staat eigenlijk een soort 3D-versie van Pythagoras! Bij gewoon Pythagoras nam je twee zijden in kwadraat en dan kreeg je de derde schuine zijde in het kwadraat, hier neem je drie oppervlaktes in het kwadraat en dan krijg je de derde "schuine"  oppervlakte in het kwadraat. (voor een bewijs van deze uiterst komische stelling moet je hier maar kijken)

     

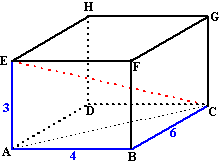
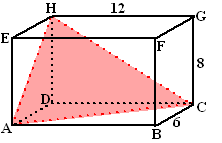
  a.  Bereken de oppervlakte van vlak AHC in de balk hiernaast.
   

√4176
  b. Hoe lang zouden HG, EF, AB en DC  van de balk moeten zijn als vlak ACH oppervlakte 49 moet hebben?
   

√73
 
       
4. De "afstand" tussen twee kleuren.

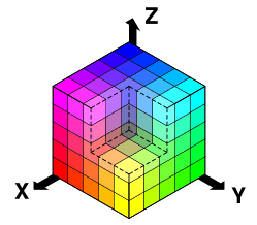
Omdat alle kleuren opgebouwd zijn uit de basiskleuren rood, groen en blauw kun je ze tekenen in een 3D assenstelsel zoals hiernaast. De waarden op elke as lopen van 0 tot en met 255. Daarbij is zwart het punt  (0,0,0) en wit het punt  (255, 255, 255).

Hieronder zie je vijf kleuren met hun hoeveelheden rood, groen en blauw.
     
 

       
  Je ziet dat de laatste twee bijna niet met het oog van elkaar te onderscheiden zijn. Het oog is onbetrouwbaar. Daarom is het handig om met Pythagoras de "afstand" tussen deze twee kleuren uit te rekenen.
Dat zou hier zijn  √(02 + 52 + 52) ≈  7,1.

Hier zie je steeds series van 10 kleuren. Eéntje is anders dan de andere negen.

     
   

       
  Vergelijk jouw keuzes met de goede oplossingen hieronder en bereken van de goede oplossingen met Pythagoras welke "kleurenafstand" je hebt geraden.
       
 
nr. 1 2 3 4 5 6 7 8
afwijkende 3 4 9 5 2 1 6 3
Rood-groen blauw  
  basis-9:
afwijkende:		 (232,74,244)
(233,74,246)		 (80,180,239)
(82,178,238)		 (247,129,72)
(246,127,75)		 (217,223,96)
(220,221,99)		 (147,242,77)
(150,246,75)		 (70,249,151)
(75,247,154)		 (233,215,86)
(238,211,82)		 (200,119,64)
(205,115,170)
       
 
nr. 9 10 11 12 13 14 15 16
afwijkende: 8 5 2 7 7 10 6 3
Rood-groen-blauw  
  basis-9:
afwijkende:		 (186,116,203)
(191,112,210)		 (213,157,106)
(208,154,98)		 (240,220,79)
(235,222,89)		 (253,66,99)
(247,74,91)		 (94,202,225)
(104,210,219)		 (126,123,196)
(116,131,190)		 (162,174,145)
(170,165,155)		 (255,255,100)
(255,80,0)
       
 

afwijkingen: 2,2 - 3,0 - 3,7 - 4,5 - 5,3 - 6,2 - 7,5 - 8,8 - 9,5 - 10,2 - 11,4 - 12,8 - 13,4 - 14,1 - 15,6 - 201,6
       
5. examenvraagstuk HAVO Wiskunde B, 2017-I
       
  De wig van Wallis is een bijzonder ruimtelijk lichaam, zie de foto.
In een bepaalde stand geldt: het zijaanzicht is een vierkant, het vooraanzicht is een gelijkbenige driehoek en het bovenaanzicht is cirkelvormig.
De constructie van een wig van Wallis met hoogte 8 is als volgt:

  - Neem als grondvlak een cirkel met straal 4.
  - Loodrecht op de cirkel komt een vierkant ABCD van 8 bij 8. De zijde AB van dit vierkant is een middellijn van de cirkel.
  - Loodrecht op zowel de cirkel als het vierkant komen allemaal gelijkbenige driehoeken. Deze driehoeken hebben hun top op het lijnstuk CD. De overige twee hoekpunten van elk van deze driehoeken liggen op de cirkel in het grondvlak.
  - Alle opstaande zijden van deze driehoeken vormen samen met AD en BC de mantel van de wig van Wallis.
       
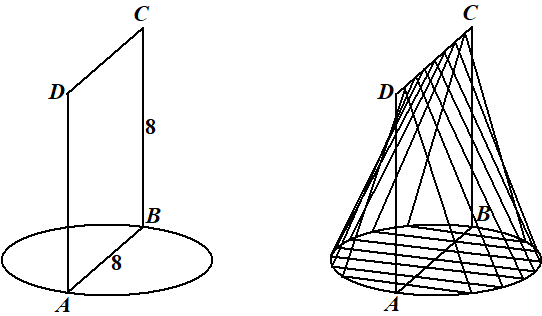
  In de volgende twee  figuren wordt de constructie van de wig van Wallis geďllustreerd.
       
 

       
  Niet alle opstaande lijnstukken die de mantel van de wig van Wallis vormen, zijn even lang.
       
  a. Bereken exact de verhouding tussen de lengte van een kortste lijnstuk en de lengte van een langste lijnstuk.
     

8 : √80
  De volgende vraag gaat over een wig van Wallis waarvan de hoogte 8,0 cm is.

Punt Q ligt op lijnstuk AB op een afstand van 1,0 cm van punt A. De wig van Wallis wordt verticaal doorsneden loodrecht op lijnstuk AB en door punt Q.
       
  b. Teken de doorsnede op ware grootte. Licht je werkwijze toe.
       
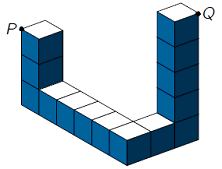
6. Vlaamse Olympiade

De kubussen in de constructie hebben ribbe 1.
Waaraan is PQ gelijk?
 
     

7
     

© h.hofstede (h.hofstede@hogeland.nl)