© h.hofstede (h.hofstede@hogeland.nl)
De afstand van een punt tot een lijn.
   
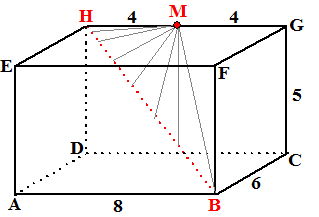
Stel dat we in de balk hiernaast de afstand van punt M tot lijn HB willen berekenen.
Dan zijn er natuurlijk allerlei mogelijke "afstanden" van M naar HB te tekenen. Kijk maar naar de grijze lijntjes in de figuur.

De vraag:  Welke van al die afstanden moeten we hebben?

Het antwoord:   De kortste!!

Als we het voortaan hebben over "DE" afstand van een punt tot een lijn dan bedoelen we daarmee de kortste afstand.
Blijft dus de vraag :  welke van al die grijze lijntjes is de kortste?
   
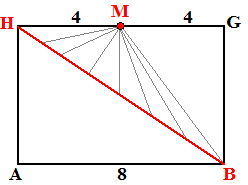
Het antwoord daarop kun je het makkelijkst vinden door het vlak waar punt M en lijn H in liggen even plat neer te leggen. In de figuur is dat vlak HGBA.

Daarin is duidelijker te zien welk lijntje nou het kortst is.

Ik hoop dat je met  me eens bent dat dat het lijntje is dat loodrecht op BH staat.  Als je dat niet vindt, of je wilt daar nog wel eens een uitgebreidere uitleg/onderbouwing van, dan moet je het bewijs hiernaast maar even lezen.

 
Wij gaan intussen verder zonder jou.....  
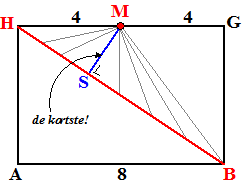
Omdat dat loodrechte blauwe lijntje inderdaad het kortste is, is de afstand van punt M tot lijn HB dus gelijk aan MS.
Daarmee hebben we een "recept" om in twee stappen de afstand van een punt tot een lijn te berekenen:
 
afstand van een punt P tot een lijn l:

1.  teken het vlak waar P en l in liggen plat.
2.  teken het lijnstuk van P loodrecht op l 
 

   
Laten we het voorbeeld nog even afmaken. het is namelijk nog helemaal niet zo eenvoudig om MS in deze figuur te berekenen. Meestal moet je op zoek gaan naar gelijkvormige driehoeken. En die zijn er hier!
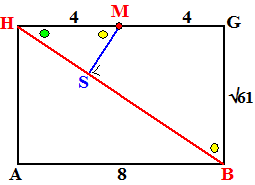
De twee gele hoeken in de figuur hiernaast zijn gelijk. Immers:
•  in ΔHMS geldt  geel + groen = 90º
•  in ΔHBG geldt  geel + groen  = 90º
Dus moeten die beide hoeken wel hetzelfde zijn.

Maar dat betekent dat de driehoeken HBG en HMS gelijkvormig zijn.
Dus kun je een verhoudingsschema maken.
Daarbij kun je gebruiken dat GB = √61 (gebruik Pythagoras in het rechterzijvlak van de balk).
Verder is dan  HB = √125 (Pythagoras in DHBG).

Dat geeft het volgende verhoudingsschema:  
   
HB
√125		 BG
√61		 HG
8
HM
4		 MS
?		 HS
 
   
En daaruit volgt vrij eenvoudig dat  MS = √61 · 4/√125  ≈ 2,79
   
De hoogtelijn van een driehoek.

Bij berekeningen van dit soort afstanden kom je vaak het probleem tegen van een driehoek waarvan je de drie zijden weet en waarvan je de hoogtelijn moet uitrekenen (dat is dan die loodrechte afstand).
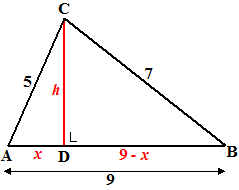
Daarom maar even een voorbeeldje daarvan.
Hiernaast zie je driehoek AC met hoogtelijn CD, en de zijden zoals aangegeven.

In driehoek ADC geldt:  x2 + h2 = 52   dus  h2 = 25 - x2
In driehoek CBD geldt:  (9 - x)2 + h2 = 72  dus  h2 = 49 - (9 - x)2 

Gelijkstellen:   25 - x2 = 49 - (9 - x)2
⇒  25 - x2 = 49 - 81 + 18x - x2
⇒  18x = 57
⇒   x = 57/18

Dan is  h2 = 25 - x2 =  25 - (57/18)2 ≈ 14,97
En dus is  h ≈ √14,97  ≈ 3,87

Nou, zo gaat dat dus.....


 
   
   
  OPGAVEN
   
1.

       
  Hierboven staat een balk ABCD.EFGH met AB = 16 en BC = 12 en CG = 5
M is het midden van HG en N is het midden van AD.
Bereken in twee decimalen nauwkeurig de volgende afstanden.
       
  a. punt B tot lijn HG

13
  b. punt H tot lijn AC.
10,82
  c. punt M tot lijn HB.

5,04
  d. punt N tot lijn BG.

16,17
  e. punt M tot lijn NB.

9,80
  f. punt N tot lijn MC.

10,39
       
2. Hiernaast staat een regelmatige vierzijdige piramide, waarvan het grondvlak ribben van 6 heeft, en waarvan de hoogte gelijk is aan 8.
M is het midden van AT.
Bereken in twee decimalen nauwkeurig de volgende afstanden:
     
  a. d(A, TC)

7,50
  b. d(M, BC)

6,02
  c. d(T, MC)

4,52
     
     
       
3. Gegeven is een regelmatig driezijdig prisma ABC.DEF met
AB = BC = CA = 4 en   BE = 8.
M is het midden van DE.
Bereken in twee decimalen nauwkeurig de volgende afstanden:
     
  a. d(A, BF)

3,90
  b. d(M, BC)

8,19
       
     

© h.hofstede (h.hofstede@hogeland.nl)