|
|||||
| Boek IV, propositie 15. | |||||
|
|||||
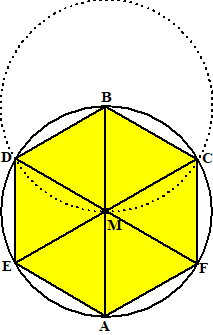
| Teken een middellijn
AB van de cirkel. Teken het middelpunt M Teken een cirkel met middelpunt B en straal MB en noem de snijpunten met de eerste cirkel C en D Teken DM en CM en verleng die tot DF en CE. Dan is AFCBDE de ingeschreven zeshoek. MD = MC = MB (eerste cirkel) BD = BC = MB (tweede cirkel) Dus ze zijn allemaal gelijk. De driehoeken MDB en MBC zijn gelijkzijdig en alle hoeken zijn 60º Dan is hoek CMF ook 60º (gestrekte hoek DF) Op deze manier zijn alle hoeken bij M 60º Bij gelijk hoeken horen gelijke bogen en koorden (III-26) (III-29) Dus BD = BC = CF = FA = AE = ED |
|
||||
| Boog AE = boog DB Tel bij beiden boog AFCB op: boog EAFCB = boog DBCFA Dan zijn hun omtrekshoeken gelijk en dat zijn de hoeken EDB en DEA (III-27) Op deze manier zijn alle hoeken van de zeshoek gelijk. Het is dus een regelmatige zeshoek. |
|||||
| Gevolgen. | |||||
| • | De zijden van de zeshoek zijn dus gelijk aan de straal van de cirkel. | ||||
| • | Net als bij de vijfhoek kun je de omgeschreven zeshoek tekenen door de raaklijnen in de hoekpunten aan de cirkel te tekenen. | ||||
| • | Op dezelfde manier als bij de vijfhoek kun je bij een gegeven regelmatige zeshoek de ingeschreven en omgeschreven cirkel tekenen. | ||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||