© h.hofstede (h.hofstede@hogeland.nl)

Boek III, propositie 31.
       

De omtrekshoek in een halve cirkel is 90º
De omtrekshoek in meer dan een halve cirkel is minder dan 90º
De omtrekshoek in minder dan een halve cirkel is meer dan 90º
       
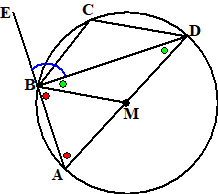
Teken een cirkel met middelpunt M, middellijn AD en een willekeurige koorde BD.

MB = MA (straal cirkel) dus de rode hoeken zijn gelijk.  (I-5)
MB = MD  (straal cirkel) dus de groene hoeken zijn gelijk. (I-5)

De blauwe hoek is gelijk aan een rode plus een groene (buitenhoek) (I-32)
Bij punt B vormen twee dezelfde hoeken (beiden rood + groen) samen een gestrekte hoek. Dus is elk 90º.
Dus de omtrekshoek van middellijn AD is 90º.

Dus is de rode hoek A minder dan 90º en dat is de omtrekshoek van BD in meer dan een halve cirkel.

ABCD is een koordenvierhoek, dus als de hoek bij A minder dan 90º is, dan is de hoek bij C meer dan 90º (samen zijn ze 180º) (III-22)
En dat is de omtrekshoek van BD in minder dan een halve cirkel.

       
Euclides vermeldt ook nog dat de hoeken die de koorde met de cirkel zelf maken "aan de kant van meer dan een halve cirkel"  groter dan 90º is en "aan de kant van minder dan een halve cirkel"  minder dan 90º. Dat volgt direct uit het feit dat de hoek ABD zelf precies 90º is
       

© h.hofstede (h.hofstede@hogeland.nl)