© h.hofstede (h.hofstede@hogeland.nl)

Boek III, propositie 16.
       
Kies een willekeurig punt A op een cirkel.
1. De rechte lijn loodrecht op MA valt buiten de cirkel
2. In de ruimte tussen die lijn en de cirkelomtrek kan niet nog een andere rechte lijn getekend worden.
3. De hoek tussen boog BA en de middellijn BA is groter dan elke scherpe hoek.
       
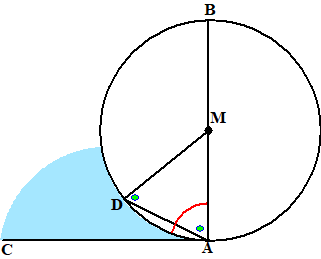
Drie stellingen:
1. Lijn AC loodrecht op MA valt buiten de cirkel.
2. In het blauwe gebied is niet nog een lijn AE te tekenen.
3. De rode hoek is groter dan elke scherpe hoek.

Stelling 1.
Stel dat AC binnen de cirkel valt, bijvoorbeeld als AD.
MD = MA  (straal cirkel) dus de groene hoeken zijn gelijk  (I-5)
Maar de ene groene hoek bij A is 90º
Dus de andere ook, en dan hebben we een driehoek met twee hoeken van 90º, en dat is onmogelijk  (I-17)
Dus AC ligt buiten de cirkel.

 
       
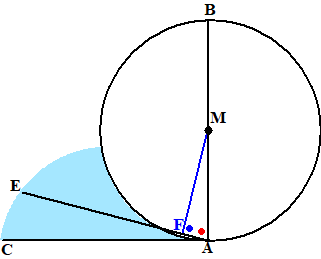
Stelling 2.
Stel dat er in die ruimte een andere lijn AE kan worden getekend.
Teken MF loodrecht op die lijn AE.

De blauwe hoek is 90º en de rode hoek is minder dan 90º  (I-17)
Dus is MF kleiner dan MA  (de grotere zijde zit tegenover de grotere hoek)  (I-19)
Maar als F buiten de cirkel ligt, dan is juist MF groter dan FA  (straal van de cirkel)
Dat is onmogelijk, dus is zo'n lijn AE niet te tekenen.
 
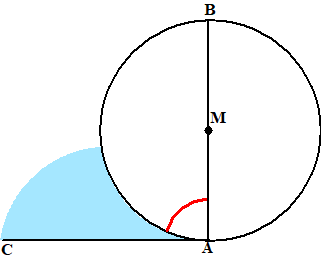
Stelling 3.
Hoek MAC is 90º, dus als die rode hoek kleiner dan een scherpe hoek zou zijn dan zou er ruimte zijn voor een lijn AE.
Dat kan niet, dus is de rode hoek groter dan elke scherpe hoek.

 
       
Belangrijk gevolg;
       

Een lijn loodrecht op MA is een raaklijn.
       
 
       
Euclides begeeft zich hier nogal op glad ijs als hij het heeft over de hoek tussen een kromme en een rechte. Hij heeft het eigenlijk over infinitesimale hoeken (en dus limieten).  Gelukkig is dit de enige propositie in de Elementen waarin hoeken met kromme benen voorkomen.
       

© h.hofstede (h.hofstede@hogeland.nl)