| |
 |
| De Poissonverdeling. |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
De Poissonverdeling is eigenlijk
een waardeloze verdeling!
Zo. Dat is een mooi didactisch verantwoord begin van een les......
Maar ja, het is nou eenmaal niet anders. Bij een Poissonverdeling zijn
er gewoon niet zoveel dingen bekend. |
| Je gebruikt een Poissonverdeling
in het volgende geval: |
| |
|
"Dingen" gebeuren
met een bekend
gemiddelde,
en onafhankelijk van elkaar. |
|
| |
Kijk, bij een binomiale verdeling
weet je veel meer: je weet om hoeveel experimenten het gaat (n) en
wat de kans per keer is (p) en dan kun je de kans op k
successen berekenen.
Het gemiddelde weet je bij de binomiale verdeling
natuurlijk ook: dat is n ·
p.
De Poissonverdeling is eigenlijk een uitgeklede binomiale verdeling.
Je kunt hem er zelfs uit afleiden. Dat gaat zó: |
| |
|
|
|
Laten we beginnen met een
voorbeeldje, waarbij er alleen een gemiddelde bekend is.
Stel dat we bekijken hoeveel kasten een antiekhandelaar per week
verkoopt. Stel dat hij een week 6 dagen van 6 uur werkt, en dat
hij weet dat hij gemiddeld per week 4 kasten verkoopt.
Hoe groot is dan de kans dat hij in één bepaalde week precies 2 kasten
verkoopt?
Laten we het aantal kasten dat hij per dag verkoopt
binomiaal bekijken. Ik verdeel de week dus in 6 gelijke stukken van een
dag, en beschouw elke dag als een experiment.
Dan is n = 6
en omdat het gemiddeld aantal kasten per week 4 is, is 6 p =
4 dus p = 2/3
De kans dat hij 2 kasten verkoopt in zes dagen is dan
binompdf(6, 2/3,
2) = 0,0823
Laten we nu het aantal kasten dat hij per uur verkoopt
binomiaal bekijken. Ik verdeel een week dan in 36 gelijke stukken van
een uur en beschouw elk uur als een experiment. Dan is n = 36 en
dan is 36 p = 4 dus p =
4/36
De kans dat hij dan 2 kasten verkoopt bij deze 36 experimenten is
binompdf(36, 4/36,
2) = 0,1418
Laten we nu het aantal kasten dat hij per kwartier
verkoopt binomiaal bekijken. Ik verdeel een week dan in 144 gelijke
stukken van een kwartier. Dan is n = 144 en dan is
144 p = 4 dus p = 4/144
De kans dat hij dan 2 kasten verkoopt bij deze 144 experimenten is
binomdf(144, 4/144,
2) = 0,1455
Laten we nu het aantal kasten dat hij per minuut verkoopt
binomiaal bekijken. Ik verdeel een week dan in 2160 gelijke stukken van
een minuut en beschouw elke minuut als een experiment. Dan is n =
2160 en dan is 210 p = 4 dus p =
4/2160.
De kans dat hij dan 2 kasten verkoopt bij deze 2160 experimenten is
binompdf (2160, 4/2160,
2) = 0,1465
En zo kan ik steeds kleinere tijdseenheden nemen......
De kansen die er uitkomen lopen naar een bepaalde limietwaarde, en dat
is de kans die de Poissonverdeling
berekent.
Noem het gemiddelde (in dat geval 4) gelijk aan m en het
gevraagde aantal successen (in dit geval 2) gelijk aan k, dan
geldt: |
| |
|
|
|
|
|
| |
|
|
|
Dat is met k = 2 en m = 4 gelijk aan 42/2!
e-4 = 0,146525111...
Het voordeel is dat je bij dit bovenstaande verhaal nergens n of
p nodig hebt voor de berekening van deze uiteindelijke kans.
Alleen n p is voldoende......
De afleiding van deze prachtige formule staat in de verdieping
hiernaast. |
| |
|
|
 |
|
Waar kun je 'm voor gebruiken? |
| |
|
|
|
Er moeten wel een paar
voorwaarden zijn om de Poissonverdeling te mogen gebruiken. Op de eerste
plaats moet het gaan om discrete gebeurtenissen ("successen" net als bij
de binomiale verdeling).
Verder moet het ook mogelijk zijn om hele kleine tijdsintervallen te
nemen. Je moet n heel groot kunnen laten worden (en dus p
heel klein zodat n p constant blijft).
Als het verkopen van een kast in het voorbeeld hierboven bijvoorbeeld
een uur zou kosten, dan kun je moeilijk gaan onderverdelen in minuten,
want in 2 opvolgende minuten kun je dan nooit beide een kast verkopen.
Verschillende minuten in de buurt van elkaar zijn dan niet
onafhankelijke experimenten meer, en dat is wel nodig voor de
binomiale verdeling.
Voorbeeld 1.
Je hebt een radioactief materiaal waarvan je weet dat er
gemiddeld 3 kernen per minuut vervallen. Hoe groot is dan de kans dat er
6 kernen in een minuut vervallen?
oplossing : m = 3 (per minuut), dus de
Poissonverdeling geeft P(6) = 36/6! e-3
= 0,0504
Voorbeeld 2.
Op een autoweg komen er gemiddeld 10 auto's per minuut
langs. Hoe groot is de kans dat er in een minuut 15 auto's
langskomen?
oplossing: m = 10 (per minuut), dus de
Poissonverdeling geeft P(15) = 1015/15! e-10
= 0,0347
N.B. Wat in de tijd geldt, kan ook in
de ruimte gelden natuurlijk, kijk maar:
Voorbeeld 3.
Een automobilist weet dat hij langs een bepaalde snelweg
gemiddeld 4 dode dieren zal zien per 5 kilometer
Hoe groot is de kans dat hij op één kilometer 2 dieren zal zien?
oplossing: m = 4/5
= 0,8 (per km), dus de Poissonverdeling geeft P(2) = 0,82
/2! e-0,8 = 0,1437
andere tijdsintervallen. |
| |
|
|
|
| Voor het aantal successen op
interval [0, t] vervang je gewoon m door
tm: |
| |
|
|
|
|
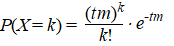 |
| |
|
|
|
| Om bijvoorbeeld in bovenstaand
"kasten" voorbeeld (met gemiddeld 4 kasten in een week) te
berekenen hoe groot de kans is dat je 20 kasten in een maand verkoopt,
neem je tm = 4 4 = 16, en dat geeft P(x = 20) = 1620/20!
e-16 = 0,0559 |
| |
|
|
|
|
met de GR. |
| |
|
|
|
Het kan ook direct met je GR:
2nd - DISTR - D : poissonpdf geeft met
λ = m = 4 en x value = 2 de kans
0,1465... precies zoals in het oorspronkelijke voorbeeld bovenaan.
En voor 20 kasten in een maand doe je poissonpdf(16, 20) =
0,0559...
En net zoals bij de binomiale verdeling is er ook een cumulatieve
poissonverdeling met de knop poissoncdf.
Als het gemiddelde in een periode gelijk is aan 5 en je wilt
bijvoorbeeld de kans op minstens 8 successen weten, dan bereken je
P(X ≥ 8) = 1 - P(X ≤ 7) = 1
- poissoncdf(5, 7) = 0,1334 |
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Ik krijg per dag gemiddeld (dat heb ik lange
tijd bijgehouden) 8 telefoontjes.
Hoeveel dagen per jaar zal ik dan naar verwachting precies 12
telefoontjes krijgen? |
| |
|
|
|
| 2. |
In een
bepaald gebied zijn gemiddeld 5 blikseminslagen per jaar.
Bereken de kans dat er in een jaar minder dan 3 blikseminslagen
zijn. |
| |
|
|
|
| 3. |
Een student
Nederlands is er trots op dat hij vrij goed zonder spelfouten
kan schrijven. Hij blijkt gemiddeld slechts 1 spelfout per 8
bladzijden tekst te maken.
Hoe groot is dan de kans dat een bladzijde precies 1 spelfout
bevat? |
| |
|
|
|
| 4. |
Een
Nederlands echtpaar heeft nog gemiddeld slechts 8 keer per jaar
seks met elkaar.
Hoe groot is de kans dat ze deze maand precies 2 keer seks met
elkaar zullen hebben? |
| |
|
|
|
| 5. |
De volgende tabel geeft het aantal
hartinfarcten dat per maand in een bejaardentehuis plaatsvindt: |
| |
|
|
|
| |
| aantal infarcten |
aantal keer |
0
1
2
3
4
5
6
>6 |
4
11
13
10
7
3
2
0 |
|
| |
|
|
|
| |
Onderzoek of dit aantal infarcten
een Poissonverdeling volgt. |
|
| |
|
|
|
| 6. |
De klantenbalie van een bouwmarkt is 8 uur per
dag open (van 9:00 tot 17:00) en er komen gemiddeld per
dag 25 mensen bij de balie.
Hoe groot is de kans dat er op een dag na 15:00 nog
meer dan 8 mensen langskomen? |
| |
|
|
|
| 7. |
In een kartonnagefabriek treden
regelmatig storingen op omdat het karton vastloopt in de
machine. De bedrijfsleider heeft bijgehouden dat er gemiddeld 3
storingen per uur optreden.
Hoe groot is dan de kans dat er over een hele dag (8 uur) minder
dan 15 storingen optreden? |
| |
|
|
|
| 8. |
a. |
Een leraar van een middelbare school
geeft gemiddeld per week 3 leerlingen strafwerk.
Hoe groot is de kans dat hij in een maand dan minstens 10
leerlingen strafwerk geeft? |
| |
|
|
|
| |
b. |
Een collega berekent dat de kans dat
zij minstens 12 keer in een maand strafwerk geeft gelijk is aan
30%.
Hoeveel leerlingen geeft zij dan gemiddeld per week strafwerk? |
| |
|
|
|
| 9. |
In Noord-Oost Groningen vinden de
laatste jaren regelmatig aardbevingen plaats ten gevolge van de
aardgaswinning.
Het gemiddelde aantal aardbevingen is 2 per maand.
Hoe goot is de kans dat er binnen één week dan meer dan 1
aardbeving plaatsvindt? |
| |
|
|
|
| 10. |
In een bepaalde
erg beruchte klas op een middelbare school worden de leerlingen
er erg vaak uitgestuurd, namelijk gemiddelde met z'n allen 24
keer per maand!
De klas bestaat uit 28 leerlingen en ze hebben 80 lessen in de
maand.
Neem aan dat iedereen iedere les aanwezig is, en dat je per les
per persoon hoogstens één keer eruit gestuurd kunt worden. |
| |
|
|
|
| |
a. |
Hoe groot
is de kans dat er in een bepaalde maand zelfs 30 keer iemand
uitgestuurd wordt?
Bereken deze kans op twee manieren: met de
poissonverdeling en met de binomiale verdeling. |
| |
|
|
|
| |
Marenthe is
de ergste uit de klas. De kans dat zij er in een maand minstens
5 keer uitgestuurd wordt is 80% |
| |
|
|
|
| |
b. |
Bereken het
gemiddeld aantal keren dat Marenthe eruit gestuurd wordt.
Bereken dit gemiddelde op twee manieren: met de
poissonverdeling en met de binomiale verdeling. |
| |
|
|
|
| |
|
|
|
|
|
De Standaarddeviatie. |
| |
|
|
|
Als je de Poissonverdeling als
grensgeval van de binomiale verdeling afleidt, dan kun je de
standaarddeviatie van de Poissonverdeling natuurlijk vast ook wel van de
standaardafwijking van de binomiale verdeling afleiden.
Voor de binomiale verdeling gold
σ =
√(n p (1 - p))
De Poissonverdeling nam m = n p constant en
liet n steeds groter worden, en p steeds kleiner. Dus p
gaat naar nul, en n naar oneindig (np = m constant).
Maar als p naar nul gaat, dan gaat (1 - p) naar 1.
Dan staat er
σ =
√(n p 1) =
√m |
| |
|
|
|
|
|
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|