|
|
 |
|
Functie en Parameterkromme. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
We hebben intussen twee
verschillende manieren om een kromme te beschrijven. De eerste is met
een formule y = .... (en dan komt er iets met x-en) en dat
heet ook wel een "functievoorschrift". De tweede manier is natuurlijk
met een parameterkromme (schrijf x en y allebei als
functie van een parameter t).
De vraag van vandaag:
| |
| "Kunnen we die twee manieren in elkaar
omzetten?" |
| |
Daar staan eigenlijk TWEE vragen:
Vraag 1: is er een manier om van een functievoorschrift een
parametervoorstelling te maken?
Vraag 2: is er een manier om van een parametervoorstelling
een functievoorschrift te maken? |
|
|
Vraag 1.
JA!
Dat is zó eenvoudig dat ik je niet zal beledigen door dat nog uit te
gaan leggen.
Vraag 2.
Dat is wat lastiger te zeggen. Dat het niet altijd
mogelijk is, kun je al wel zien aan de "ingewikkelde"grafieken die we
zijn tegengekomen bij parametervoorstellingen. |
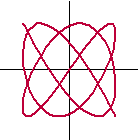
Neem de figuur hiernaast die
hoort bij de zo simpele vergelijkingen x = sin(5t)
en y
= sin(7t).
Daar kun je nooit één formule van maken, want het probleem met formules
van de vorm y = .... is, dat er bij elke ingevoerde x
hoogstens één y uitkomt.
Soms kunnen we de boel nog een beetje bedriegen met functies als y
= ± ..... zodat er tenminste twee y-en
kunnen uitkomen, maar in de figuur hiernaast komen er bij sommige
x-en wel VIJF y-en uit! Dat lukt nooit....
Maar ja, soms lukt het ook wél. Neem de
volgende parametervoorstelling: |
 |
|
|
|
Kijk, je kunt zó redeneren:
"Als x gelijk is aan t, dan mag ik elke t dus ook
wel door x vervangen. Als ik dat doe in de tweede vergelijking
dan staat daar y = x2 - 4x en dat is een
functievoorschrift. Klaar!"
"Bah", zul je waarschijnlijk zeggen, "Wat een kinderachtig en flauw
voorbeeld! Toevállig omdat daar precies staat x = t.
FLAUW!! Dat werkt bij élke formule die achter y staat".
Klopt. Ik heb het voorbeeld hier alleen genoemd omdat ik zin had je te
beledigen. Hier staat namelijk het antwoord op vraag 1 hierboven!!!
Immers zo kun je van een willekeurige formule voor y een
parametervoorstelling maken door er x = t aan toe
te voegen.
Toch geeft de aanpak wel een aanwijzing hoe het in andere gevallen zou
kunnen....
Kijk, je hebt dus te maken met twee vergelijkingen met drie letters (x,
y, en t) en je wilt graag één vergelijking met twee
letters (x en y). Die t moet weg.
Dat kan als volgt:
• stap 1: maak van de x-vergelijking t =
.......
• stap 2: vul dat wat nu op die stippeltjes staat in de y-vergelijking
in plaats van elke t in.
Het probleem is dat stap 1 vaak niet of nauwelijks te doen is, en dan
loopt het al meteen vast.
Een tweede probleem is, dat de y-vergelijking er wel wat raar kan
uitzien.Voorbeeld van de beide problemen... |
Neem de parametervoorstelling:
|
|
stap 1: Hoe maak je van x =
cos(2t) iets als t = .....?
Om die cos daar weg te krijgen zul je toch de inverse van cos moeten
gebruiken; de cos-1x van je rekenmachine.
Dat geeft 2t = cos-1(x) dus
t = 1/2cos-1(x)
stap 2: Invullen in de y-vergelijking geeft y = sin2(1/2cos-1x)
Nou, het is gelukt, maar het geeft wel een nogal rare vergelijking. En
als je de parametervoorstelling of deze vergelijking plot, dan zie je
dat de grafiek verdacht veel lijkt op een rechte lijn!!!! Zo te zien de
lijn y = 1/2
- 1/2x |
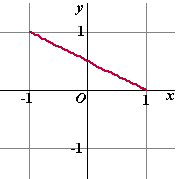 |
|
|
Kunnen we dat misschien bewijzen?
In het vervolg gebruik ik de notatie ?=? Daar bedoel ik mee: "Wat
hier staat moet nog bewezen worden". Dat helpt wel eens, want
als je met ingewikkelde bewijzen bezig bent wil je halverwege nog wel
eens vergeten wat je ook al weer aan 't doen was....
Dus ons probleem is: y ?=?
1/2
- 1/2x
Laten we zowel y als x vervangen door de formule uit
de parametervoorstelling. Dat heeft als voordeel dat we nog maar één
letter overhouden (de t):
sin2t ?=? 1/2
- 1/2cos(2t)
Maar er geldt cos(2t) = 1 - 2sin2t
(een oude van vroeger)
⇒ sin2t
?=? 1/2
- 1/2(1
- 2sin2t)
⇒ sin2t
?=? 1/2
- 1/2
+ sin2t
⇒ sin2t
?=? sin2t
We komen uit op iets dat voor elke t geldt, dus geldt de
oorspronkelijke formule ook voor elke t. Daarmee is hij bewezen. |
|
|
| Samengevat: er zijn drie
manieren om van een parametervoorstelling een functievoorschrift te
maken: |
|
|
| 1. Als het
functievoorschrift gegeven is, en je moet het bewijzen. |
| |
Vervang elke y door de
y(t) formule en elke x door de x(t)
formule. Dat geeft één formule met als enige letter de
t. Probeer deze formule te bewijzen. |
| |
|
|
| 2. Als het
functievoorschrift niet gegeven is. |
| |
a. |
De basisaanpak is: verander x
= .... in t = .....
Vervang de t's in, in de y-vergelijking door
deze nieuwe formule. |
| |
b. |
Je kunt ook proberen de kromme te plotten,
het goede functievoorschrift te "raden" en dan met methode
1. te bewijzen dat je inderdaad goed hebt geraden. |
|
| |
|
|
OPGAVEN |
|
|
| 1. |
Gegeven is een parameterkromme K door de
vergelijkingen x(t) = 2sin2(t)
en y(t) = sin2(2t)
Toon aan dat de kromme K een deel van de grafiek van y
= 2x - x2 is. |
| |
|
|
|
| 2. |
Gegeven is een parameterkromme K door de
vergelijkingen x(t) = 2t
- 4 en
y(t) = t2 + t
Geef een functievoorschrift voor deze kromme. |
| |
|
|
|
| 3. |
Gegeven is een parameterkromme K door de
vergelijkingen x(t) = sin(t) en
y(t) = sin(3t)
Toon aan dat de kromme K een deel van de grafiek van y
= 3x - 4x3 is.
(tip: bedenk dat je sin(3t) kunt
schrijven als sin(2t + t) ) |
| |
|
|
|
| 4. |
Gegeven is een parameterkromme K door de
vergelijkingen x(t) = 3/(t
- 1) en y(t) =
√t
Geef een functievoorschrift voor deze kromme. |
| |
|
|
|
| 5. |
Gegeven is een parameterkromme K door de
vergelijkingen x(t) = sin(t +
1/4π)
en y(t) = sin(2t)
Toon aan dat de kromme K een deel van de grafiek van y
= 2x2 - 1 is. |
| |
|
|
|
| 6. |
Gegeven is een parameterkromme K door de
vergelijkingen: |
| |
|
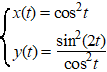 |
| |
Geef een functievoorschrift voor de grafiek waar
deze kromme een deel van is. |
| |
|
|
|
| 7. |
Gegeven is de kromme K door: x(t) = sin(t
- 0,25π)
en y(t) = sin 2t
Daarin is t element van [a , b] |
| |
|
|
|
| |
a. |
Plot K en geef de coördinaten van de keerpunten |
| |
|
|
|
| |
b. |
Kies [a , b] zodanig dat de kromme
precies één keer doorlopen wordt. |
| |
|
|
|
| |
c. |
Bij K hoort een formule van de vorm y = px2
+ q. Leid uit de figuur de waarden van p en q af. |
| |
|
|
|
| |
d. |
Toon algebraïsch aan dat de bij c) gevonden formule
juist is. |
| |
|
|
|
| 8. |
Gegeven is de kromme K door: x(t) = 2·sin t
en
y(t) = sin(2t - 0,5π)
Plot K.
Welke formule hoort vermoedelijk bij K? Toon aan dat
deze formule juist is. |
| |
|
|
|
| 9. |
Gegeven is de kromme K door: x(t) = sin t
en
y(t) = sin 2t met t in [0,2π]
Toon aan dat bij K de formule y2 = 4x2
- 4x4 hoort. |
| |
|
|
|
| 10. |
De baan van punt P wordt gegeven door: x(t) = sin(t
- 0,25π)
en y(t) = sin22t
Met t in [-0.25π ,
0.75π]. Hierin
zijn x en y in cm en t in seconden.
De baan van punt P kan ook gegeven worden
door de formule y = 1 - 4x2 + 4x4
met x in [-1 , 1] |
| |
|
|
|
| |
a. |
Toon dat aan. |
|
| |
|
|
|
| |
b. |
Schets de grafiek van de snelheid van punt P als
functie van t. |
| |
|
|
|
| |
c. |
Wat is de maximale snelheid van P? |
| |
|
|
|
 |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
|
|
|
|
|
|
|
|