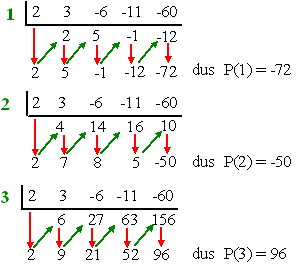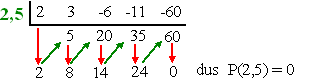Nulpunten van polynomen.

© h.hofstede (h.hofstede@hogeland.nl)

     



synthetisch delen.
Waarschuwing vooraf:  Deze les is er echt eentje voor algebra-liefhebbers.
Alle berekeningen kunnen met een GR tien keer sneller, maar de echte wiskundige zal dat natuurlijk niet bevredigend genoeg vinden, hoop ik.

Je bent dus gewaarschuwd; laten we beginnen.

Een polynoom is een functie die er zó uitziet:   f(x) = an · xn +  an - 1 · xn - 1 +  .... + a0
Ofwel: het zijn allemaal termen die uit gehele machten van x bestaan.

Nou is er een erg handige stelling die ons kan helpen om nulpunten van dit soort functies te vinden.
Dat is deze stelling:
       

als een breuk x = p/q  een nulpunt van een polynoom  
an · xn +  an - 1 · xn - 1  +  .... + a0 is,
waarvan de coëfficiënten gehele getallen zijn,  
dan is  p een deler van a0  en q een deler van an
       
Waarom is dat zo?

Nou, als x =  p/q  een nulpunt is, dan is het polynoom te schrijven als:
an · xn +  an - 1 · xn - 1 +  .... + a0 =  (qx - p) ·(bn - 1 · xn - 1 + bn - 2 ·  xn - 2 +  .... + b0)
Als je dan de haakjes wegwerkt krijg je als hoogste macht natuurlijk weer xn maar de coëfficiënt daarvan is  q · bn - 1  en dat moet dus gelijk zijn aan an . Omdat dat gehele getallen zijn is q een deler van an
Volgens dezelfde redenatie wordt de term zonder macht van x (eigenlijk met x0) gelijk aan   p · b0  en dat moet gelijk zijn aan a0, dus is p een deler van a0.

Wat heb je d'r aan?

Deze eigenschap kan je helpen om zulke nulpunten op te sporen. Als je de delers van a0 en van an bekijkt, dan weet je alvast welke breuken eventueel  als nulpunt in aanmerking komen.
Met synthetisch delen (hoe dat werkt staat uitgelegd in deze les) kun je dan snel controleren of ze inderdaad kloppen.

Voorbeeld
Zoek algebraïsch een nulpunt van  y = 2x4 + 3x3 - 6x2 - 11x - 60

De delers van an = 2  zijn  ±1 en ±2  en de delers van  a0 = -60 zijn  ±1, ±2, ±3, ±5,  ±6, ±10, ±12, ±20, ±30 en  ±60   
Dat geeft maar liefst 40 mogelijke breuken:   ±1/±1 en ±1/±2 en ±2/±1 en ±2/±2 en ±3/±1 en ±3/±2 en ..... en ±60/±1 en ±60/±2
Dat zijn de getallen:  ±1, ±1/2, ±2, ±3, ±11/2, ±5, ±21/2, ±6, ±10, ±12, ±20, ±30, ±15, ±60 
en dat zijn 28 mogelijke nulpunten.

Laten we ze allemaal gaan uitproberen, te beginnen met de gehele getallen.
Daarvoor moet je eigenlijk elke keer een staartdeling maken en kijken of er geen rest overblijft, maar het kan sneller met synthetisch delen.
De eerste paar:

       
Helaas, nog geen rest NUL, dus nog geen nulpunten. Maar voordat je nu als een blindeman verder gaan proberen, moet je iets opvallen....  JUIST!   Je ziet hierboven dat  P(2) = -50  en  P(3) = 96  dus het polynoom wisselt tussen x = 2 en x = 3 van teken, dus daar moet een nulpunt zitten! En de enige mogelijkheid uit de lijst is 21/2.
Laten we daarom direct 21/2 proberen:

       
YES!   x = 21/2 is inderdaad een nulpunt, en het polynoom is te schrijven als   (x - 21/2) • (2x3 + 8x2 + 14x + 24)

Als je zou willen kun je nu het zelfde proces weer gaan toepassen op  2x3 + 8x2 + 14x + 24 door de delers van 2 en 24 te nemen. Dan vind je misschien nog meer nulpunten  (ik zal vast verraden dat x = -3 er ook eentje is).
Ik wou het hier maar bij laten, het idee is wel duidelijk denk ik.
       
         
1. a. Zoek een nulpunt van f(x) = 2x3 - 2x2 + 6x - 6
       

x = 1
  b. Zoek een nulpunt van f(x) = 4x4 - 4x3 + 5x2 + 34x - 18
       

x = 1/2
  c. Zoek een nulpunt van  f(x) = 5x5 - 2x4 + 10x3 - 9x2 - 3x + 2
       

x = 2/5
         
       

© h.hofstede (h.hofstede@hogeland.nl)