|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Synthetisch delen is een handig
maniertje voor als je een polynoom moet delen door (x - p)
met p één of ander getal. (een polynoom ziet er uit als a + bx + cx2 + dx3 + .....) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
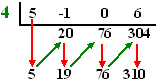
| Dat is er dus zo eentje. Schrijf nu eerst de coëfficiënten bij de machten van x op een rijtje neer van hoge macht naar lage macht. Denk eraan dat een macht die mist eigenlijk coëfficiënt NUL heeft. In dit voorbeeld geeft dat het rijtje: 5 -1 0 6 Zet dat getal p ervoor, met voor de duidelijkheid een streep tussen p en de coëfficiënten. Dat geeft dus 4 | 5 -1 0 6 Het volgende schemaatje laat nu zien hoe ontzettend simpel synthetisch delen werkt. Volg gewoon de pijlen!!!! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De rode
pijlen staan voor het optellen van de getallen die onder
elkaar staan. De groene pijlen staan voor vermenigvuldigen met p (in dit geval 4). Daar op de onderste rij vind je nu precies de coëfficiënten van het antwoord, met op het eind de rest. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| of ook : 5x3 - x2 + 6 = (x - 4) • (5x2 + 19x + 76) + 310, dat is hetzelfde natuurlijk. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
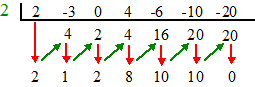
| Voorbeeld. Onderzoek of 2x6 - 3x5 + 4x3 - 6x2 - 10x - 20 nul oplevert als x = 2 Als dat zo is, dan is die formule deelbaar door (x - 2) dus moet er bij delen rest nul uitkomen: Synthetisch delen: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Er komt inderdaad rest nul uit, dus de gegeven formule levert nul op bij x = 2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Delen door "iets anders lineairs". | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Als je moet delen door x
+ p dan schrijf je dat gewoon als x
- (-p)
. Dus dan komt daar linksboven in het schema een negatief getal te
staan. Verder niks aan de hand. En als je moet delen door bijvoorbeeld 2x - 4 dan zou ik dat schrijven als 2(x - 2) en dan eerst delen door x - 2 en in het antwoord daarvan nog eens alles door 2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
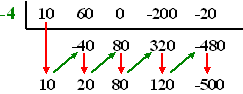
| Voorbeeld:
Deel 10x4 + 60x3
- 200x - 20 door 2x + 8 2x + 8 = 2(x + 4) We delen daarom eerst alles door x + 4 = x - (-4). Dat geeft dit schema: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vervolgens delen we die coëfficiënten 10, 20, 80, 120 en -500 allemaal nog door 2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Waarom werkt dit? Tja, daar moet je eigenlijk de les over staartdelingen voor doen. Daar is dit een speciale notatie van. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
