Doe de normaal-test!

© h.hofstede (h.hofstede@hogeland.nl)
 

We weten nu dat de normale verdeling ongeveer zo'n klokvorm geeft, maar er zijn zovéél histogrammen die ongeveer zo'n vorm hebben. Hoe kun je nou onderzoeken of ze wel precies aan die moeilijke formule van Gauss voldoen?  Neem de volgende drie histogrammen:
 

 
Welk van de drie geeft een echte klokvorm?
Het zijn allemaal  wel ongeveer klokvormen. De vraag is eigenlijk of de kromming van de  klokvorm past bij een normale verdeling. Er is gelukkig een eenvoudige methode om dat te onderzoeken. Daarvoor moet je wel weten wat een cumulatief frequentiepolygoon is. Als je dat bent vergeten neem dan eerst deze les weer door. Onthoud de volgende zaken:
 
1.  De frequenties moeten in procenten.
2.  De stippen staan bij het rechter-klasseneinde.
 
Als je van een normale verdeling een cumulatief frequentiepolygoon tekent dan krijg je een soort S-vormige kromme (zie hiernaast). Daarmee gaan we een gedachte-experiment uitvoeren........
Teken die S-kromme op een stuk rubber.
Spijker het midden horizontaal vast op een plank, en rek het rubber daarna ietsje uit. Omhoog en omlaag.
Spijker het daarna ook ietsje boven en onder het midden vast, en rek de uiteinden nog wat verder uit.
Ga zo alsmaar door: spijker vast en rek uit, spijker vast en rek uit, spijker vast en rek uit....
Als je dat een beetje handig en nauwkeurig doet dan kun je er voor zorgen dat de S-kromme verandert in een rechte lijn!
Natuurlijk heeft jouw rubberpapier dan wel een beetje rare y-as gekregen.

 

Er is papier dat zó gemaakt is dat cumulatieve normale verdelingen op dat papier rechte lijnen opleveren. Dat papier heet heel toepasselijk normaal-waarschijnlijkheids-papier (meestal zeg je gewoon normaal-papier) HIER kun je een velletje bewonderen. Let op de vreemde verdeling van de y-as: Vanaf het midden naar boven en naar beneden toe is de schaal steeds verder "uitgerekt".
Laten we de drie histogrammen van het begin van deze les meteen gaan testen.
Maak de gegevens cumulatief en in procenten. Dat geeft de volgende drie tabellen:
rechter
klasseneinde		 cumulatieve
frequentie
6
7
8
9
10
11
12		 7
16
31
50
69
84
93
 
rechter
klasseneinde		 cumulatieve
frequentie
6
7
8
9
10
11
12		 2
12
30
50
70
88
98
 
rechter
klasseneinde		 cumulatieve
frequentie
6
7
8
9
10
11
12		 2
5
15
50
85
95
98
         
En dat geeft op normaalpapier de volgende drie grafieken:

Zo te zien hoort het eerste histogram bij een "echte"  klokvorm. Dat geeft namelijk op normaalpapier het mooist een rechte lijn. In de andere twee zit een soort van kromming.

Er valt nog iets op......

De klasse >12 konden we niet tekenen omdat immers de rechtergrens onbekend is. Maar dat geeft niet. Ook al was die grens wél bekend, dan konden we het punt nóg niet tekenen. Dat komt omdat 100% niet op de y-as van ons normaalpapier te vinden is! In theorie loopt zo'n klokvorm namelijk aan beide kanten oneindig ver door. De x-as is een horizontale asymptoot. Dus liggen 0% en 100% oneindig ver omlaag en omhoog. Dat papier is steeds meer en meer uitgerekt.
 
 
100% en 0% zijn op normaalpapier niet te vinden.
 
Gemiddelde en Standaarddeviatie.
Als je zo'n histogram eenmaal op normaalpapier hebt getekend kun je uit die grafiek het gemiddelde en de standaarddeviatie vrij eenvoudig aflezen.
Het gemiddelde dat kun je zelf wel verzinnen hoop ik; dat zit uiteraard bij 50% want omdat de klokvorm symmetrisch is, is het gemiddelde gelijk aan de mediaan en dus zit 50% van de metingen daar onder.
De standaarddeviatie kun je vinden als je de figuur hiernaast weer even voor ogen haalt. Tussen μ+σ en  μ-σ zat 68% van de meetwaarden. Dat betekent dat onder m-σ  nog 16% zit, en boven  m+σ ook.

Kortom:  μ-σ kun je vinden bij 16% en  μ+σ bij 100-16 = 84%.
σ  is dan uiteraard de horizontale afstand tussen μ en μ+σ .
Dat zie je samengevat in de figuur hiernaast.

Uit die figuur blijkt ook meteen dat σ  in feite de helling van de lijn bepaalt: hoe groter σ, des te kleiner de helling. Twee normale verdeling met dezelfde standaarddeviatie zullen op normaalpapier evenwijdige grafieken opleveren. Dat kun je handig gebruiken bij opgaven als deze:

voorbeeld:
Van een normaal verdeelde grootheid is 10% kleiner dan 40 en de standaarddeviatie is 12. Bepaal met normaalpapier hoeveel procent groter is dan 60.
 

Teken op normaalpapier een lijn met een willekeurig gemiddelde en met standaarddeviatie 12.
Bijvoorbeeld een lijn door (40, 50%) en (52, 84%).
Teken vervolgens door het punt (40, 10%) een tweede lijn evenwijdig aan de eerste. Deze tweede lijn heeft dan ook standaarddeviatie 12. Lees op deze lijn bij 60 af hoeveel procent kleiner dan 60 is. Dan weet je ook hoeveel procent groter dan 60 is. (Doe het zelf maar, er komt ongeveer 65% uit).
   
  OPGAVEN
   
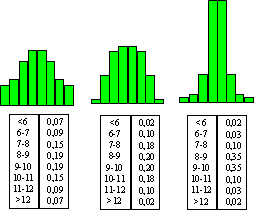
1. Onderzoek of de volgende tabellen een normale verdeling beschrijven.
         
 
meting <35 35-42 42-49 49-56 56-63 63-70 >70
frequentie 9 128 514 611 215 22 1
         
 
meting 0-8 8-16 16-24 24-32 32-40 40-48 48-56 56-64 64-72
frequentie 6 9 45 540 1200 600 300 180 120
         
2. De volgende tabel beschrijft een normale verdeling.
         
 
meting 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100
frequentie (%) 2,2 4,9 10,1 16,5 20,5 19,5 14,0 7,7 4,6
         
  Bereken van deze verdeling het gemiddelde en de standaarddeviatie. Doe dat op twee manieren:
       
  a. Met de functie STAT-CALC van je rekenmachine.  
       
  b. Met normaal-waarschijnlijkheidspapier  
         
3. Het gewicht van de eieren die de kippen op een kippenfarm leggen is normaal verdeeld.
8% van de eieren is lichter dan 58 gram en 21% is zwaarder dan 69 gram.
Bepaal het gemiddelde en de standaarddeviatie van deze eieren.
       

μ = 65, σ = 5
   
4. De vleugelspanwijdte van de volwassen zeearend is normaal verdeeld met een standaarddeviatie van 15 cm..
9% van de vogels blijkt een spanwijdte van meer dan 250 cm te hebben.
Hoeveel procent zal dan een spanwijdte van minder dan 200 cm hebben?
Onderzoek dat met behulp van normaal-waarschijnlijkheidspapier.
       

2,3%
   
5. Een nieuw onderdeel op de volgende winterspelen zal de 4 × 500 meter estafette schaatsen zijn. Nederland zal vertegenwoordigd worden door de sprinters  Bos, Wennemars, van Velde en Nijenhuis. De persoonlijke tijden van deze schaatsers zijn normaal verdeeld. De gegevens staan in onderstaande tabel. Neem voor de rest van deze opgave aan dat deze gegevens kloppen.
         
 
schaatser gemiddelde standaardafwijking
Bos 35,65 0,4
Wennemars 34,78 0,3
Van Velde 34,98 0,5
Nijenhuis 35,70 0,2
         
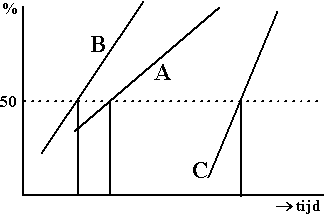
  De figuur hiernaast geeft de tijden van Wennemars, van Velde en Nijenhuis op normaal waarschijnlijkheidspapier.

Leg uit welke lijn bij welke schaatser hoort.

Neem de figuur over en schets de lijn die bij Bos hoort erbij in.

         
6. De voedselgigant MACDONALDS heeft iets nieuws: de "Supermegamac". Deze hamburger is nog groter dan alle voorgaande, en verder geen flauwekul meer met groenvoer erop. Gewoon vlees, vlees en nog meer vlees met als enig toevoegsel een lekkere vette lading mayonaise. De consumentenman vertrouwt het zaakje niet, en controleert de supermegamacs nauwgezet. Uit de totale dagvoorraad van de MACDONALDS-vestiging in de Herestraat heeft men 250 supermegamacs onderzocht. Het aantal coli-bacteriën en deze macs is gemeten, en die blijken normaal verdeeld te zijn. Daarom worden de resultaten van deze proef op normaal-waarschijnlijkheidspapier weergegeven. Het blijkt een rechte lijn door (510,4) en (690,97) te worden.
         
  a. Teken die lijn en geef met deze figuur een schatting van het aantal macs dat tussen de 525 en 660 bacteriën bevatte. Geef ook een schatting voor de standaarddeviatie van het aantal bacteriën
       

82,5%, 49.6
  Neem aan dat elke dag geldt: het aantal bacteriën in de voorraad van die dag is normaal verdeeld met een standaarddeviatie van 50. Het gemiddeld aantal (μ) hangt van een aantal factoren af, en is onbekend. Omdat MACDONALDS beweert dat zijn hamburgers van goede kwaliteit zijn, wil men dat hoogstens 7% van de hamburgers uit een dagvoorraad meer dan 500 bacteriën bevat.
         
  b. Bereken de grootste waarde van μ waarvoor dit nog het geval is.
       

426
         
7. examenvraagstuk VWO wiskunde A, 1987.

In 1787 en 1788 schreven Alexander Hamilton en James Madison de zogenaamde The Federalist Papers, om de inwoners van New York te overreden de Constitutie te ratificeren. Beide schrijvers ondertekenden met "Publius".
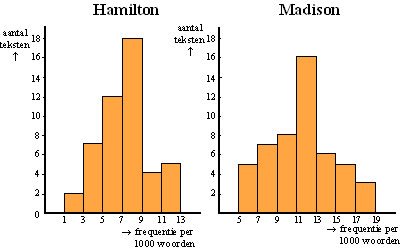
Van 48 van deze teksten is bekend dat zij van Hamilton zijn en van 50 dat zijn van Madison zijn. Om ook van de overige teksten de auteur te achterhalen, heeft men van diverse woorden geteld hoe vaak ze in een tekst van Hamilton voorkomen en hoe vaak in een tekst van Madison. Voor elk van die teksten heeft men daarna de frequentie per 1000 woorden berekend.
Dit heeft men onder andere gedaan voor het woordje "by".
Het resultaat is weergegeven in onderstaande histogrammen.
         
 

         
  Verwerk deze gegeven, zowel voor Hamilton als voor Madison, op normaal-waarschijnlijkheidspapier. Neem aan dat men mag concluderen dat de frequenties normaal verdeeld zijn. Geef dan in beide gevallen het gemiddelde en de standaarddeviatie.
         
8. examenvraagstuk VWO Wiskunde A, 1987.

Onderstaande tabel is afkomstig  uit het Statistisch Zakboek 1983 van het Centraal Bureau voor de Statistiek.

         
 
Dienstplichtigen naar lichaamslengte
  17,5 jarigen
1982
Lengte in cm
<160
160 - 164
165 - 169
170 - 174
175 - 179
180 - 184
185 - 189
190 - 194
195 - 199
200 en meer		 percentage dienstplichtigen
0,2
0,9
4,1
12,9
25,1
28,5
18,7
7,4
1,8
0,4
aantal dienstplichtigen (abs.): 105.897
gemiddelde lengte (cm): 180,7
Bron: Inspectie Geneeskundige Dienst Koninklijke Landmacht
         
  a. Toon met normaal-waarschijnlijkheidspapier aan dat de lichaamslengten vrijwel normaal verdeeld zijn; controleer of het vermelde gemiddelde juist is en bepaal de standaarddeviatie.
         
  Voor de marechaussee geldt een minimumlengte van 170 cm en voor de luchtmacht een maximumlengte van 193 cm
         
  b. Bereken het percentage van de dienstplichtigen van wie de lengte zowel geen belemmering is voor dienst bij de marechaussee als bij de luchtmacht (in gehele procenten nauwkeurig)
         
9. examenvraagstuk VWO Wiskunde A, 1984.

De researchafdeling van een fabriek heeft een nieuw type batterij ontwikkeld, dat bijzonder geschikt is voor het aandrijven van speelgoedmotortjes. In de fabriek wordt de eerste dagen de productie nauwgezet gecontroleerd. Daarbij let men vooral op de levensduur van de batterijen bij aanhoudende belasting. Uit de totale productie van de eerste dag heeft men aselect 250 batterijen genomen en aan een duurproef onderworpen. Het aantal 'lege' batterijen is geregistreerd na perioden van steeds 30 minuten. De ervaring leert dat de levensduur van de batterijen uit een dagproductie vrijwel normaal verdeeld is. Daarom zijn de resultaten van de duurproef op het normaal-waarschijnlijkheidspapier hieronder weergegeven.

         
 

         
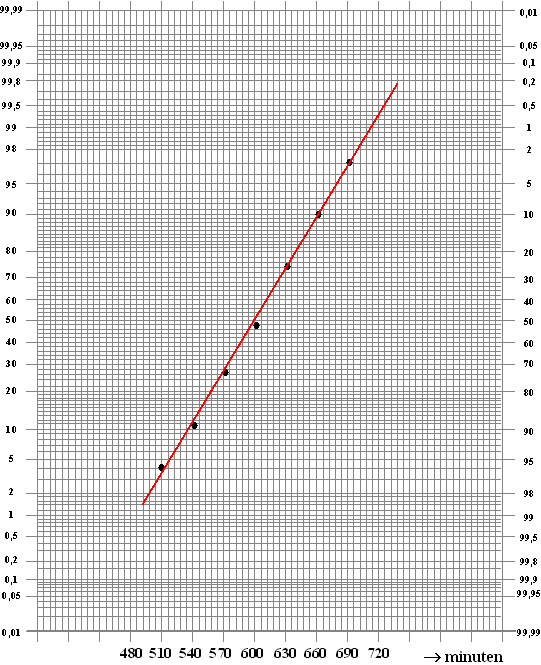  a. Geef met behulp van deze figuur een schatting van het percentage batterijen van de gehele dagproductie waarvoor de levensduur tussen 8,75 en 11 uur lag. Licht het antwoord toe.
         
  Neem aan dat voor elke productiedag geldt: de levensduur van die dag geproduceerde batterijen is normaal verdeeld met een standaarddeviatie van 50 minuten. Het gemiddelde (μ) in minuten is afhankelijk van een aantal factoren in het fabricatieproces.

Omdat de fabrikant in reclameboodschappen beweert dat zijn batterijen erg lang meegaan, wil hij ervoor zorgen dat hoogstens 7% van de batterijen uit de dagproductie een levensduur heeft van minder dan 8,5 uur.
         
  b. Bereken in minuten nauwkeurig de kleinste waarde van μ waarvoor dit nog het geval is.
         
10. examenvraagstuk VWO Wiskunde A, 2002.
         
  Vogels die hun voedsel in bomen en struiken zoeken doen dat vaak bij voorkeur op een specifieke hoogte.
Gedurende een winter zijn in een bos voedselzoekende vogels geobserveerd. In de tabel hieronder staat de verdeling over verschillende hoogtes van 400 waarnemingen bij pimpelmezen.
         
 
hoogte in meters <1,5 1,5 - 3 3 - 5 5 - 7 7 - 10 10 - 15 >15
aantal waarnemingen 24 26 51 72 122 92 13
         
  Toon aan dat de waargenomen hoogtes bij benadering normaal verdeeld zijn; maak gebruik van normaal waarschijnlijkheidspapier. Lees uit je tekening af hoe groot het gemiddelde en de standaardafwijking van deze verdeling zijn. Geef beide antwoorden in dm nauwkeurig. Licht je werkwijze toe.
       

76 dm - 40 dm
         
11. examenvraagstuk VWO Wiskunde A, 2008.

Een tennisballenfabrikant produceert drie types tennisballen: Yellow, Silver en Gold. Van elk type is de diameter (bij benadering) normaal verdeeld. De fabrikant geeft de diameter van een tennisbal altijd op in inches. De fabrikant heeft bij 400 tennisballen van het type Yellow de diameters laten opmeten. Het resultaat daarvan zie je in tabel 1.
         
 
400 waarnemingen bij tennisballen van het type Yellow
diameter in inches <2,4 2,4 - <2,5 2,5- <2,6 2,6- <2,7 2,7- <2,8 ³2,8
aantal waarnemingen 1 4 98 232 63 2
         
  a. Zet de gegevens uit op normaal waarschijnlijkheidspapier en toon daarmee aan dat de waargenomen diameters van Yellow inderdaad bij benadering normaal verdeeld zijn.
         
  Uit de tekening die je bij de vorige vraag hebt gemaakt kun je aflezen hoe groot het gemiddelde en de standaardafwijking van de diameter van een bal van het type Yellow is.
         
  b. Bepaal het gemiddelde en de standaardafwijking van de diameter van een bal van het type Yellow. Licht je werkwijze toe.
       

2,62 en 0,08
  Bij officiële wedstrijden mag een tennisbal niet te groot en ook niet te klein zijn. In de spelregels staat daarover het volgende:
         
 

Bij alle proeven ter bepaling van de omvang moet een omvangmeter gebruikt worden. De omvangmeter bestaat uit een metalen plaat. In de plaat zitten twee cirkelvormige openingen met een diameter van respectievelijk 2,575 inch en 2,700 inch. De bal mag niet door zijn eigen gewicht door de kleine opening vallen, maar moet wel door zijn eigen gewicht door de grootste opening vallen.
         
  Van het type Gold is de diameter (bij benadering) normaal verdeeld met een gemiddelde van 2,620 inch en een standaardafwijking van 0,048 inch. De tennisballenfabrikant krijgt de opdracht 1200 tennisballen van het type Gold te leveren die gebruikt kunnen worden bij officiële wedstrijden.
         
  c. Bereken hoeveel tennisballen de fabrikant naar verwachting moet produceren om aan deze opdracht te voldoen.
       

1543
         

© h.hofstede (h.hofstede@hogeland.nl)