|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. | a. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
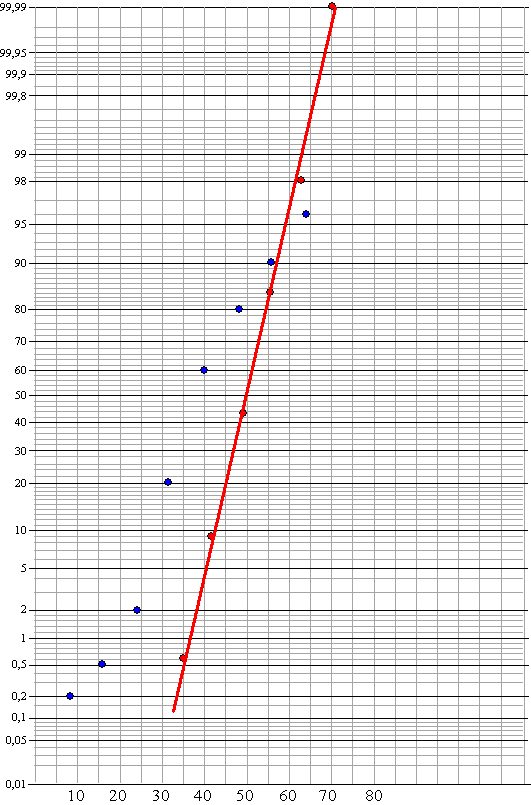
| zie de rode lijn in de figuur
hieronder. dat ligt aardig op een rechte lijn, dus dat zal wel een normale verdeling zijn. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| zie de blauwe stippen
in de figuur hieronder. Daar gaat geen rechte lijn door dus dit zal geen normale verdeling zijn. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | a. | L1 = 15, 25, 35, ..., 95 L2 = 2.2, 4.9, 10.1, ..., 4.6 stat-calc-1Vat Stats (L1m L2) geeft gemiddelde 57,88 en standaarddeviatie 18,6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| b. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
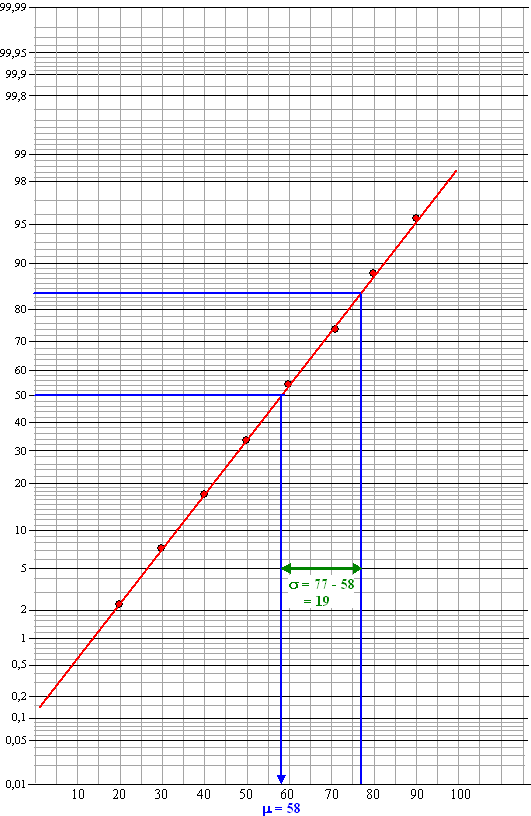
| dat geeft op normaal waarschijnlijkheidspapier: | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| μ
aflezen bij 50% en dat is ongeveer 58. σ aflezen tussen 84% en 50% en dat is ongeveer 19. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
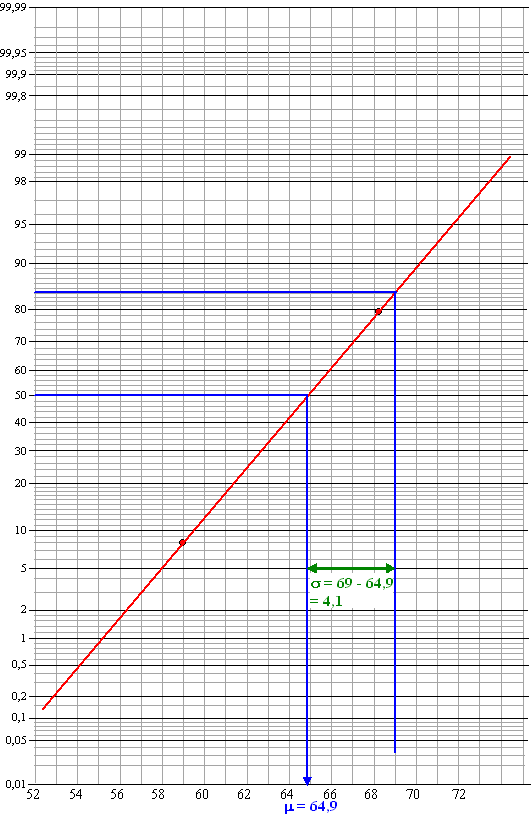
| 3. | Als 21% zwaarder is
dan 69 gram dan is dus 79% lichter dan 69 gram. De lijn op normaalpapier gaat door (69, 79) en (58, 8). Dus dat ziet er zó uit: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dat geeft μ = 64,9 en σ = 4,1 zoals je in de figuur hierboven kunt zien. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
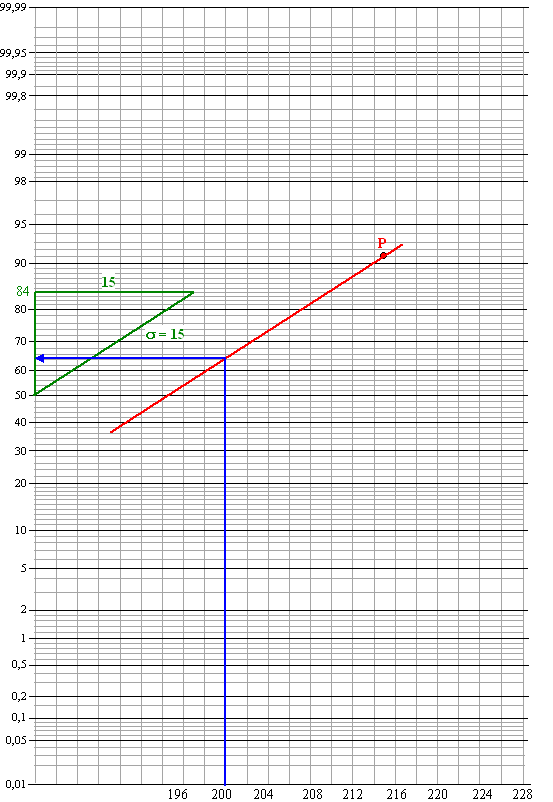
| 91% heeft minder dan
215, dus de lijn moet door punt P(215, 91%) gaan. Teken een willekeurige lijn met σ = 15. De groene lijn (tussen 50% en 84% een breedte 15) Teken dan door P de rode lijn evenwijdig aan de groene. Aflezen bij 200 cm geeft 64%. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
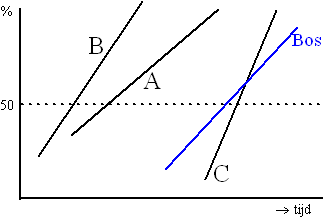
| 5. | Het gemiddelde vind je op de 50%
lijn. Wennemars heeft het laagste gemiddelde en is dus B Van Velde is dan A en Nijenhuis is C Bos heeft gemiddelde net iets minder dan Nijenhuis, dus zal net links van Nijenhuis op de 50% lijn zitten. Als de standaarddeviatie kleiner is, loopt de lijn steiler. Bos heeft standaarddeviatie 0,4 dus zijn lijn loopt steiler dan die van Van Velde (A) maar vlakker dan die van Wennemars (B) Zie de figuur hiernaast. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. | a. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
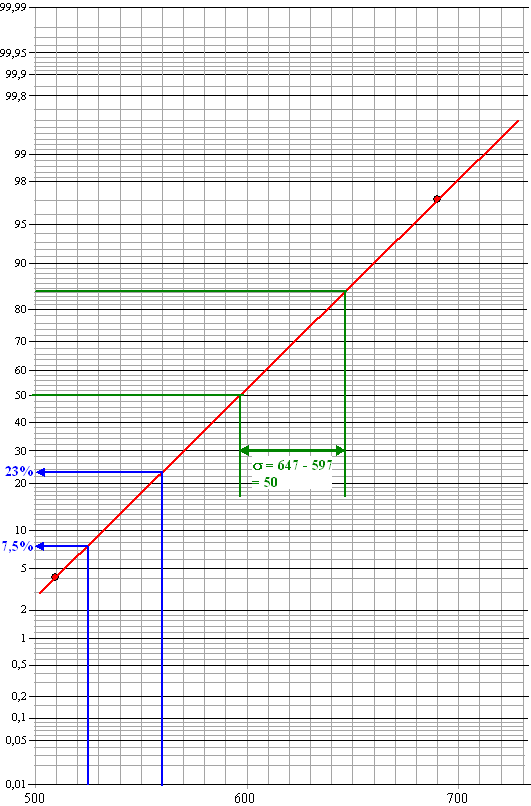
| tussen 525 en 116:
23% - 7,5% = 15,5% (blauw in de figuur) standaarddeviatie: tussen 84% en 50%: 647 - 597 = 50 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Y1 = normalcdf(500,
1099, X, 50) Y2 = 0,07 intersect geeft X = μ = 426 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. | Hamilton: | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| Madison: | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
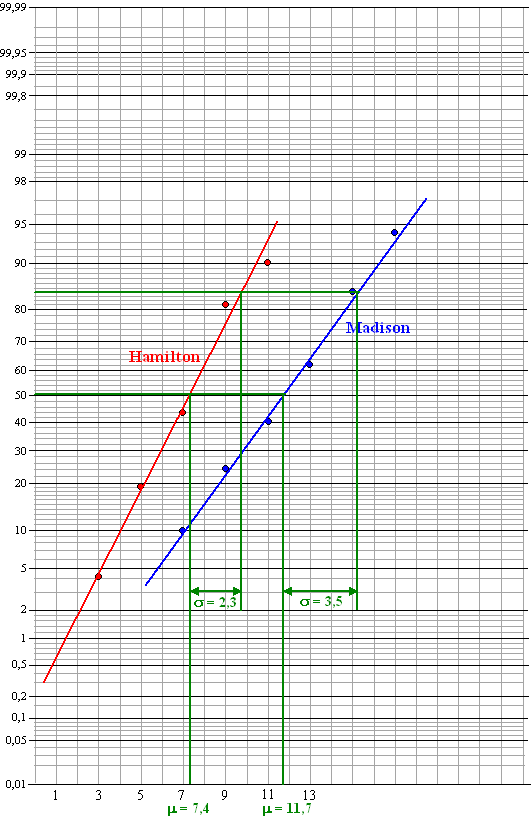
| Hamilton:
μ = 7,4 en
σ = 2,3 Madison: μ = 11,7 en σ = 3,5 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. | a. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
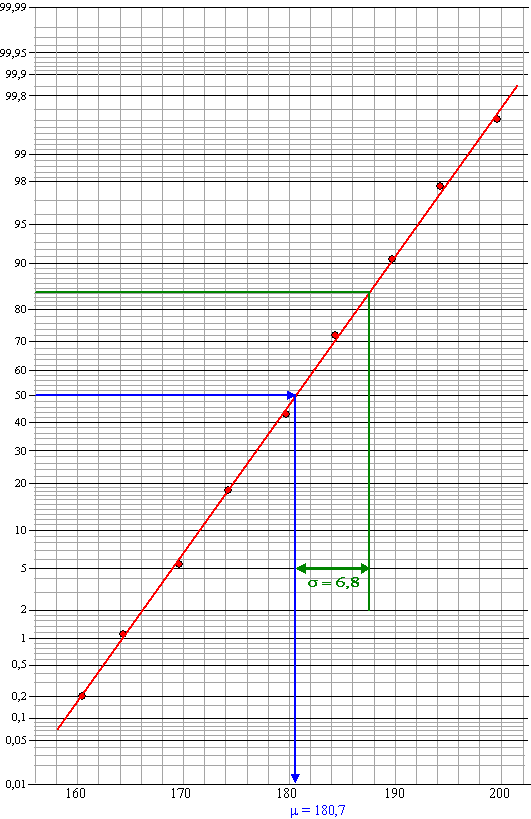
| De rechtergrenzen
zijn onder de aanname dat de lengtes afgerond zijn (en niet afgekapt). Dat geeft op normaalpapier: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| μ
= 180,7 zou goed kunnen kloppen (blauw) de standaarddeviatie (groen) is ongeveer 187,5 - 180,7 = 6,8 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | normalcdf(170, 193, 180.7, 6.8) = 0,9069 dus dat is ongeveer 91% | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. | a. | 8,75 uur is 525
minuten en daar lees je af ongeveer 6,5% 11 uur is 660 minuten en daar lees ja af ongeveer 90% Daartussen ligt dus ongeveer 83,5% |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | 8,5 uur is 510
minuten Y1 = normalcdf(0, 510, X, 50) Y2 = 0,07 intersect geeft X = μ = 583,7 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
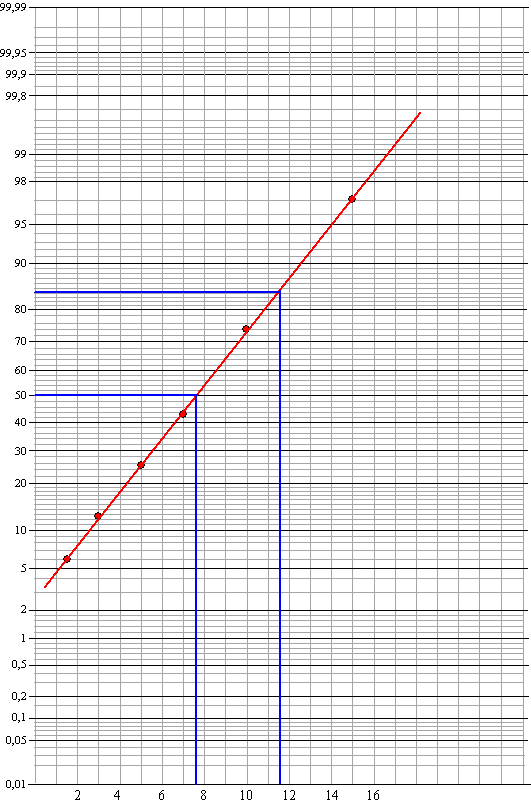
| 10. | De
grafiek moet cumulatief en in procenten. De stippen moeten bij het einde
van de klassen. De grafiek gaat dan door de punten: (1.5 , 6) (3 , 12.5) (5 , 25.25) (7 , 43.25) (10 , 73.75) en (15 , 96.75) De laatste klasse is niet te tekenen. De grafiek wordt goed een rechte lijn dus de gegevens zijn bij benadering normaal verdeeld, kijk maar: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het gemiddelde m is af te lezen bij 50% en is
ongeveer 7,6 meter dus
μ is ongeveer 76
dm Bij 84% is μ + σ af te lezen. Dat is ongeveer 11,6 meter dus 116 dm. Dus σ is ongeveer 116 - 76 = 40 dm. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. | a. | Op normaal
waarschijnlijkheidspapier staan de gegevens cumulatief en relatief (in
procenten). Omdat de gegevens cumulatief zijn staan de stippen bij de rechter klassengrenzen, dus bij 2,4 en 2,5 enz. Dit wordt de tabel cumulatief relatief: |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
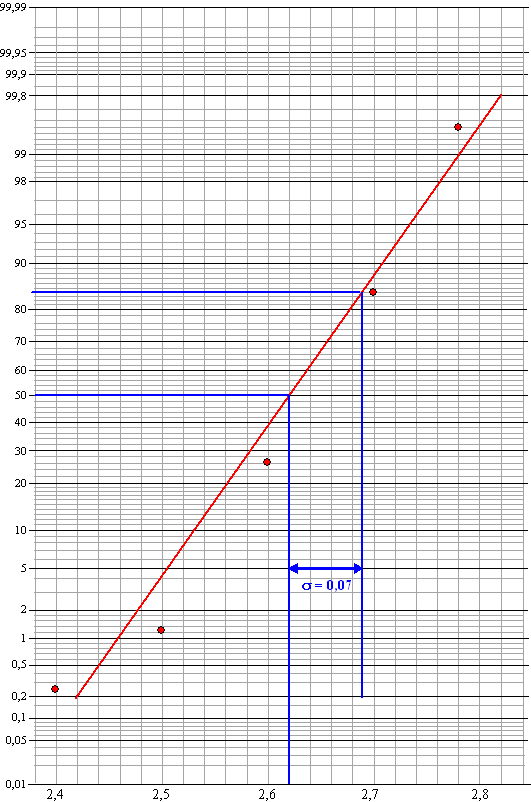
| De onderste twee rijen geven op normaal waarschijnlijkheidspapier deze grafiek (de antwoorden van vraag b staan er ook al in): | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| Zie de figuur
hierboven. Het gemiddelde vind je bij 50% en is ongeveer μ = 2,62 μ + σ vind je bij 84% en dat is ongeveer 2,69, dus σ = 2,69 - 2,62 = 0,07 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | normalcdf(2.575,
2.700, 2.620, 0,048) = 0,7780 77,80% moet gelijk zijn aan 1200 ballen. Dan is 100% gelijk aan 1200/77,80 • 100 = 1542 ballen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||