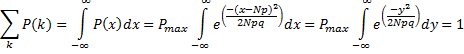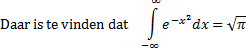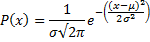| De Normale verdeling afleiden uit de Binomiale. | ||||
| Dit wordt een
behoorlijk theoretische les, waarin we zullen bekijken hoe de normale
verdeling uit de binomiale verdeling is af te leiden als N erg groot
wordt. De binomiale verdeling is: |
||||
|
|
||||
| We nemen nu eerst de natuurlijke logaritme van deze P (met gebruik van de rekenregels voor logaritmen): | ||||
|
lnP = lnN! - lnk! - ln(N - k)! + klnp + (N - k)ln(1 - p) |
||||
| Maar voor grote
waarden van x geldt dat lnx!
≈ xlnx - x
(De afleiding daarvan kun je
hier vinden). Voor de afgeleide daarvan geldt dan (productregel): (lnx!)' ≈ 1 • lnx + x • 1/x - 1 = lnx De lnP hierboven is een functie van k. Laten we de afgeleide ervan bekijken: |
||||
|
(lnP)' = -lnk + ln(N - k) + lnp - ln(1 - p) ......(1) |
||||
| Om het maximum van
lnP (en dus ook van P) te vinden stellen we die afgeleide gelijk aan
nul: -lnk + ln(N - k) + lnp - ln(1 - p) = 0 en dat kun je met de rekenregels voor logaritmen weer samennemen: |
||||
|
|
||||
| ⇒
(N - k)p = k(1 - p) ⇒ Np = kp + k(1 - p) ⇒ k = Np Oké, nog niet echt verrassend; we hebben gevonden dat P maximaal is bij het gemiddelde k = Np dus daar ligt de top van de binomiale verdeling. Nu gaan we de binomiale verdeling benaderen met een Taylorreeks rond dat gemiddelde Np: |
||||
|
f (x) = f(Np) + f '(Np) • (x - Np) + 1/2! • f ''(Np) • (x - Np)2 + 1/3! • f '''(Np) • (x - Np)3 + ..... |
||||
| (Daarbij
is die f uiteraard onze lnP, en is x gelijk aan onze k) Die eerste afgeleide wordt uiteraard nul (bij x = Np is er immers een maximum). Die tweede afgeleide is interessanter: voor (lnP)'' moeten we vergelijking (1) hierboven nog een keer naar k differentiëren: (lnP)'' = -1/k - 1/(N - k) en voor k = Np geeft dat: |
||||
|
|
||||
| De eerste drie termen
van de Taylorreeks geven dan (met q = 1 - p):
lnP = (lnPmax) - 1/(2Npq) • (x
- Np)2 Nu van beide kanten de e-macht nemen en we hebben P gevonden: |
||||
|
|
||||
| Pmax kunnen we vinden doordat we weten dat de som van alle kansen samen gelijk moet zijn aan 1. Als we die som weer benaderen door een integraal, dan geeft dat: | ||||
|
|
||||
| Die laatste integraal heet de Gauss-integraal en is in deze les te vinden. | ||||
|
|
||||
| als we x
daarin vervangen door y/√(2Npq)
dus dx = √2Npq •
dy dan geeft onze integraal dat: 1 = Pmax
• √(2πNpq) Noem tenslotte √(Npq) = σ en Np = μ, en dan wordt de formule voor P(x): |
||||
|
||||
|
|
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
||||