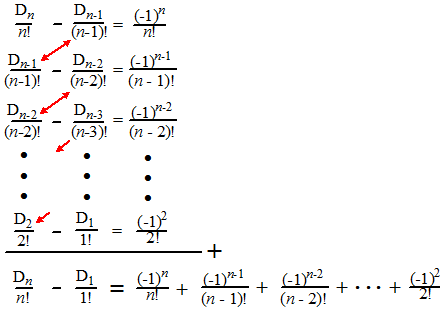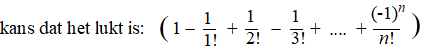lootjes trekken


Lootjes trekken.	© h.hofstede (h.hofstede@hogeland.nl)

Iedereen die ooit Sinterklaas met een groep volwassenen heeft gevierd kent ongetwijfeld dit probleem.
Er zijn een aantal (n) volwassen mensen, genaamd A, B, C, D, .... die onder elkaar een aantal lootjes genaamd a, b, c, d, ... moeten verdelen. Maar A mag niet lootje a krijgen en B niet lootje b, enz.... ofwel:

Hoe groot is de kans dat niemand zijn eigen lootje trekt?

Om die kans te berekenen gebruiken we uiteraard weer de kansdefinitie: kans = ^{aantal gunstig}/_{aantal mogelijk.}Het totaal aantal manieren om n lootjes onder n mensen te verdelen is makkelijk: dat is natuurlijk n!. (voor het eerste lootje zijn n mogelijkheden, voor het tweede lootje nog n - 1 enz.

Maar hoe groot is het aantal gunstige manieren?
Noem D_n = aantal manieren om n lootjes onder n mensen te verdelen waarbij niemand zijn eigen lootje krijgt.

Neem eerst lootje a.
Er zijn n - 1 manieren om dat lootje aan een ander persoon dan A te geven.

Stel dat lootje a aan persoon B is gegeven.
Dan zijn er twee verschillende manieren waarop lootje b kan worden toegewezen:

Lootje b wordt aan persoon A gegeven.
Dan blijven er nog over de lootjes c, d, e, ... en de personen C, D, E, ....
Die kunnen op D_{n - 2} manieren "goed" verdeeld worden.

Lootje b wordt aan een ander gegeven.
Dan blijven nog over de lootjes b, c, d, e, ... en de personen A, C, D, E, ...
Omdat b niet aan A gegeven mag worden (dat was geval 1) is het nu net alsof er n - 1 lootjes over n - 1 personen moeten worden verdeeld (je kunt persoon A wel hernoemen als "B" omdat hij niet lootje b mag krijgen).
Die kunnen op D_{n - 1} manieren "goed" verdeeld worden.

Het totaal aantal manieren waarop de lootjes b, c, d, ... verdeeld kunnen worden is dan gelijk aan D_{n - 2} + D_{n
- 1}Maar deze hele redenering ging ervan uit dat lootje a aan persoon B werd gegeven. Dat kan natuurlijk aan n - 1 personen en voor elk van die personen geldt de redenering hierboven..
Daarom geldt D_n = (n - 1) × (D_{n - 2} + D_{n - 1})
En verder is ook wel duidelijk dat D₁ = 0 en D₂ = 1 (in je eentje kun je geen lootjes trekken en met z'n tweeën is er maar één manier om ze te verdelen).

Hè Hè, we hebben een vergelijking: D_n = (n - 1) × (D_{n - 2} + D_{n
- 1}) . Hoe verder?

Haakjes wegwerken: D_n = nD_{n - 2} + nD_{n
- 1} - D_{n - 2} - D_{n - 1}.
Daar zit een soort symmetrie in. Herrangschik zó: D_n - nD_{n
- 1} = (n - 1)D_{n - 2} - D_{n - 1} = -{D_{n
- 1} - (n - 1)D_{n - 2}}
Als je nu D_n - nD_{n
- 1} een nieuwe naam geeft, bijvoorbeeld P_n dan staat daar P_n = -P_{n - 1}
Maar dan kunnen we helemaal teruggaan naar het begin:
P_n = -P_{n -
1} = (-1)² P_{n - 2} = (-1)³P_{n
- 3} = .... = (-1)^{n - 2}P₂En die P₂ kunnen we uitrekenen: P₂ = D₂ - 2D₁ = 1
Dus P_n = (-1)^{n
- 2} = (-1)ⁿ

En nu terug naar de D-wereld: D_n - nD_{n - 1} = (-1)ⁿ

Het mooie komt pas als je een serie gaat opschrijven:

Al die termen met de rode pijlen ertussen zijn gelijk, dus vallen weg als je ze allemaal optelt.
Met D₁ = 0 en die n! naar de andere kant geeft dat voor het aantal gunstige manieren om n lootjes "goed" onder n mensen te verdelen:

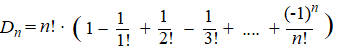Dit is het aantal gunstige manieren.
Omdat het totaal aantal manieren gelijk was aan n!, vinden we voor de kans dat het lukt:

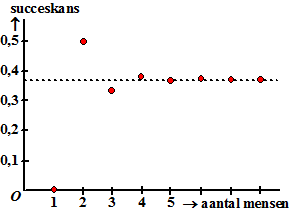
Hiernaast zie je een grafiek voor de succeskans (P) als functie van het aantal mensen (n).
Je ziet dat dat erg snel nadert naar een waarde van ongeveer 0,37.

(de echte wiskunde-experts zullen misschien zelfs zien dat die waarde exact gelijk is aan ¹/_e = 0,3678794412.....)

NAWOORD.
Als je ook nog geïnteresseerd bent in de kans op 1, 2, 3.... mensen die hun eigen lootje trekken, dan moet je deze les maar bestuderen.

OPGAVEN

Een postbode moet 6 brieven bij 6 verschillende adressen bezorgen.
Hij gooit er met de pet naar en stopt in elk van de 6 brievenbussen willekeurig één van de zes brieven.
Hoe groot is de kans dat geen enkele brief in de goede brievenbus zit?

0,3681

Een deelnemer aan een quiz moet 5 verschillende prijskaartjes bij 5 verschillende artikelen proberen te leggen.
Hoe groot is de kans dat hij er precies één goed heeft als hij volledig moet gokken?
Geef je antwoord exact.

3/8

Een gezin van 5 (twee ouders en 3 kinderen) gaan voor Sinterklaas lootjes trekken.
Hoeveel keer zullen ze dat gemiddeld moeten doen voordat niemand zijn eigen lootje heeft?
Geef je antwoord in 2 decimalen.
(voor een exact antwoord moet je eigenlijk eerst deze les doornemen)

³⁰/₁₁=2,73