oneindige kansbomen


Oneindige Kansbomen.	© h.hofstede (h.hofstede@hogeland.nl)

Sommige kansexperimenten kunnen in theorie oneindig lang doorgaan.

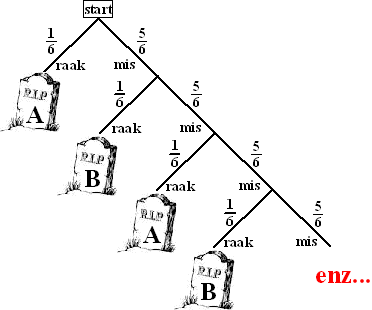
Neem bijvoorbeeld het spannende "spel" Russisch Roulette.
Dat gaat als volgt:
Twee spelers zitten tegenover elkaar met een pistool waarbij in één van de zes kamers een kogel zit.
Speler A draait een willekeurige kamer voor de loop van het pistool, zet het pistool tegen zijn slaap en haalt de trekker over. Als hij zichzelf doodschiet heeft speler B gewonnen. Als de kamer voor de loop leeg was moet nu speler B hetzelfde doen.

En dat gaat zo alsmaar verder totdat één van beide spelers zichzelf doodschiet.
Daar hoort de volgende kansboom bij:

Deze kansboom is oneindig groot! Die rechtertak gaat alsmaar verder, want er kán elke keer weer gemist worden!!
Laten we de kans dat A wint gaan opschrijven. Dat zijn dus de takken van die boom met een grafsteen voor speler B.

De kansen op die takken zijn:
⁵/₆ • ¹/₆ en ⁵/₆ • ⁵/₆ • ⁵/₆ • ¹/₆ en ⁵/₆ • ⁵/₆ •⁵/₆ • ⁵/₆ • ⁵/₆ • ¹/₆ enz.
Bij twee opeenvolgende takken komt steeds een factor ⁵/₆ • ⁵/₆ = ²⁵/₃₆.
Maar dat betekent dat dit een meetkundige rij is, met factor a = ²⁵/₃₆ en beginwaarde b = ⁵/₃₆ en voor de som daarvan geldt S = ^b/_{(1
- a)} (de afleiding daarvan staat in deze les)
In dit geval geeft dat een kans ⁵/₁₁dat A de winnaar zal zijn.

Kans-Aantal-Formules.

Een interessante vraag is natuurlijk: hoe lang zal zo'n spelletje gemiddeld duren?
Die vraag kun je op de "standaardmanier" beantwoorden door de verwachtingswaarde van het aantal schoten te berekenen. Dat wordt dan weer een oneindige rij waarvan je misschien de som kunt berekenen (misschien ook niet, ik weet niet hoe goed jij in wiskunde bent...).

Maar het kan veel leuker....en sneller....

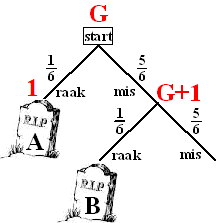
Kijk naar het begin van de kansboom.

Stel dat het spel vanaf dat begin gemiddeld G schoten zal duren.
Eén schot later zijn er dan twee mogelijkheden: Als het raak was, dan is het spel afgelopen en duurt het dus nog nul schoten.
Als het schot mis was, dan zijn we in precies dezelfde situatie als in het begin! Dat betekent dat het spel vanaf daar weer gemiddeld G schoten zal duren, dus vanaf het begin G + 1 schoten.

Maar dat betekent dat G = ¹/₆ • 0 + ⁵/₆ • (G + 1)
Daaruit vind je snel G = 6
Deze erg elegante methode heet een kans-aantal-formule (Ik noem het voortaan een KAF)

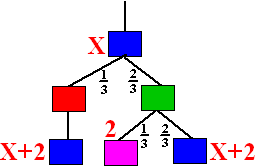
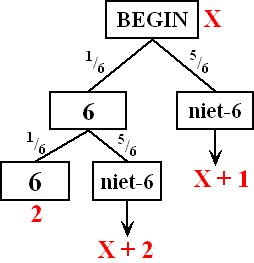
Voorbeeld.

Hoe lang duurt het gemiddeld om met een dobbelsteen twee keer achter elkaar zes te gooien?

De kansboom hiernaast geldt.

Aan de rode X-en lees je af dat:
X = ¹/₆ • ¹/₆ • 2 + ¹/₆ • ⁵/₆ • (X + 2) + ⁵/₆ • (X + 1)

Dat lost makkelijk op tot X = 42.

Prachtige methode toch??

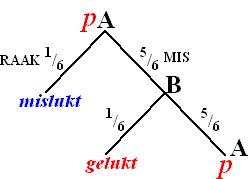
KAF's met kansen.

Maar wacht eens even...wat met gemiddelden kan dat kan natuurlijk ook met kansen.
Stel dat de kans dat russisch roulettespeler A wint p is, dan geldt in de kansboom hiernaast:
p = ⁵/₆ • ¹/₆ + ⁵/₆ • ⁵/₆ • p

Daaruit volgt meteen dat p = ⁵/₁₁

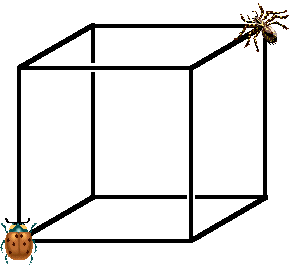
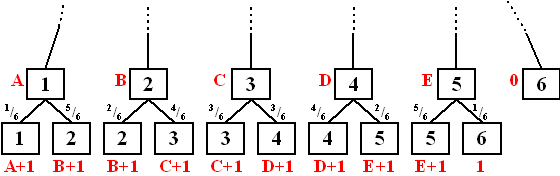
Een beroemd raadsel.

Op een hoek van een draadkubus zit een kever. Diagonaal er tegenover zit een spin. De spin blijft op zijn plaats zitten, maar de kever gaat over de ribben van de kubus kruipen. Over elke ribbe doet hij 5 minuten. Bij een hoekpunt aangekomen kiest hij willekeurig één van de drie ribben die daar samenkomen om zijn weg te vervolgen (terugkruipen kan dus ook)
Bij de spin aangekomen wordt de kever opgegeten.

Wat is de gemiddelde tijd die zo'n kever op de kubus doorbrengt?

Je kunt dit raadsel vrij eenvoudig oplossen door eens goed te kijken hoe zo'n kubus er nou schematisch uitziet:

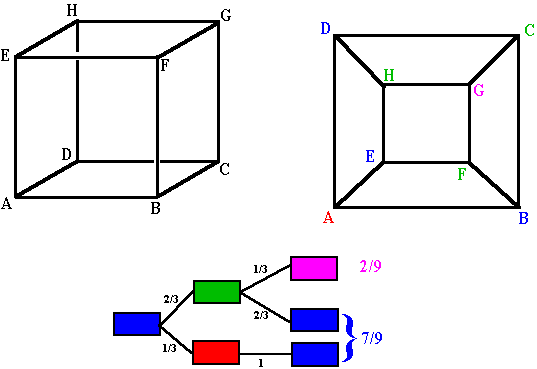
Noem de hoekpunten van de kubus ABCD.EFGH. In de figuur rechtsboven zijn de verbindingen van de hoekpunten schematisch weergegeven, maar de hoekpunten zijn verschillend gekleurd, met de volgende reden:
De kever begint op het rode hoekpunt A. Na 5 minuten is hij in ieder geval op een blauw hoekpunt. Vanaf een blauw hoekpunt kan hij naar een groen hoekpunt kruipen of naar het rode hoekpunt. Van een groen hoekpunt kan hij naar een blauw hoekpunt kruipen of naar het paarse (de spin).
We kijken dus niet naar de precieze hoekpunten waar de kever zich bevindt, maar naar de TOESTANDEN die gelijkwaardig zijn.
De mogelijke overgangen (vanaf een blauw hoekpunt) staan in de kansboom onderaan. Samengevat levert dat op, dat een kever die nu op een blauw hoekpunt staat, na 10 minuten kans ⁷/₉ heeft om weer op een blauw hoekpunt te staan, en kans ²/₉ om dood te zijn.

Uit de kansboom volgt (zie hiernaast):
X = ¹/₃(X+2) + ²/₃ • ¹/₃ • 2 + 2/₃ • 2/₃ • (X + 2)
Dat levert vrij eenvoudig op dat X = 9

Maar dat was vanaf een blauwe toestand, dus vanaf het begin kost dat gemiddeld 10 stappen; de kever leeft gemiddeld 50 minuten.

Hoe vaak zul je gemiddeld met een muntstuk moeten gooien om drie keer achter elkaar KOP te gooien?

14 keer

Spelers A en B houden een weddenschap. Ze gooien met twee dobbelstenen en kijken naar de som van beide ogen. Als dat 12 is heeft speler A gewonnen, als dat twee keer achter elkaar 7 is heeft speler B gewonnen. Als geen van beiden heeft gewonnen gooien ze steeds weer.
Hoe groot is de kans dat A wint?

⁷/₁₃

Het probleem van de verzamelaar

Stel de fabrikant van AMSTEL-bier houdt een actie: aan de onderkant van elke dop staat een letter, namelijk A, M, S, T, E of L. Wie alle letters verzameld, kan ze inleveren en daarvoor gratis een flesje AMSTEL witbier krijgen. Neem aan dat alle letters in gelijke mate over de flesjes verdeeld zijn.
De vraag is: hoeveel flesjes moet je gemiddeld openen (en eventueel leegdrinken) om alle letters te hebben?

Nou, laten we een stukje midden uit de kansboom tekenen. De getallen stellen voor hoeveel verschillende letters we op dat moment al hebben. Dat ziet er zó uit:

Bereken hoeveel flesjes de verzamelaar gemiddeld moet kopen.

14,7

Een muis heeft drie kamers om kaas in te zoeken.
Als de muis kamer 1 binnengaat zal hij de kaas na 3 minuten vinden.
Als de muis kamer 2 binnengaat zal hij 4 minuten zoeken en niets vinden. In dat geval verlaat hij de kamer.
Als de muis kamer 3 binnengaat zal hij 5 minuten zoeken en niets vinden. In dat geval verlaat hij de kamer.

Als de muis kamer 2 of 3 heeft verlaten kiest hij willekeurig een nieuwe kamer om binnen te gaan (het kan best wéér kamer 2 of 3 zijn).

Wat is de gemiddelde tijd voordat de muis kaas vindt?

12 minuten

Leuk! Een Dubbele KAF!

Die komt voor in het beroemde probleem van de knikkers van Markov. Dat luidt als volgt:

Twee spelers mogen om de beurt aselect een bal uit een bak trekken. In de bak zitten in het begin 2 groene en 8 rode ballen.
Als een speler een rode bal trekt, dan moet hij die weer terugleggen.
Als een speler een groene bal trekt, dan moet hij die houden.
Degene die de tweede groene bal pakt heeft gewonnen.

Hoe groot is de kans dat de speler die begint ook wint?

Dit wordt als je hem gaat tekenen een oneindige kansboom. Het kan immers alsmaar doorgaan (in theorie).
In die kansboom zijn er eigenblijk twee verschillende toestanden te onderscheiden:

•

toestand I: er is nog geen groene knikker getrokken (dus er zitten er nog twee in).

•

toestand II: er is al wel een groene knikker getrokken (dus er zit er nog maar eentje in).

Vanuit toestand I is er ²/₁₀ kans dat je in toestand 2 terechtkomt, en ⁸/₁₀ kans dat je in toestand I blijft.
Vanuit toestand II is er ¹/₉ kans dat je wint, en ⁸/₉ kans dat je in toestand II blijft.

Eerste KAF.

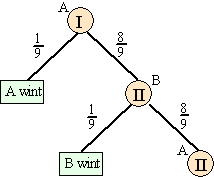
Stel dat we in toestand II zijn, en speler A is aan de beurt. Dan geldt de kansboom hiernaast.

Als de kans dat speler A in toestand II wint gelijk is aan p dan moet er gelden: ¹/₉ + ⁸/₉ • ⁸/₉ • p = p
Daaruit volgt dat p = ⁹/₁₇Conclusie

een speler in toestand II heeft ⁹/₁₇ kans om te winnen

Tweede KAF.

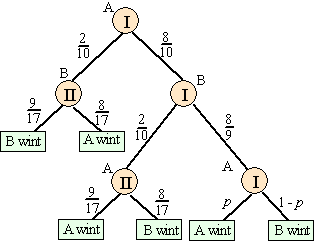
Met het resultaat hierboven in ons achterhoofd gaan we nu naar het begin van het spel, met speler A aan zet.
Daarvoor geldt de kansboom hiernaast, met die ⁹/₁₇ (en ⁸/₁₇van niet-winnen) erbij.

Stel dat de kans dat A in toestand I wint gelijk is aan p.

Dan zie je hiernaast dat moet gelden:
p = ²/₁₀ •⁸/₁₇ + ⁸/₁₀ • ²/₁₀ • ⁹/₁₇ + ⁸/₁₀ • ⁸/₉ • p

Daaruit volgt: ³⁶/₁₀₀ • p = ⁷⁶/₄₂₅
Dus p = ⁷⁶/₁₅₃≈ 0,4967....

ofwel: Je kunt beter niet beginnen!