Logaritmisch papier

© h.hofstede (h.hofstede@hogeland.nl)
Logaritmisch papier is een speciaal soort papier, waarbij één of beide coördinaatassen een logaritmische schaalverdeling hebben. Er zijn twee soorten. Als één as logaritmisch is, dan spreken we van enkellogaritmisch papier, en als beide assen logaritmisch zijn, dan heet het dubbellogaritmisch papier. Die laatste komt in de volgende les, deze les beperken we ons tot enkellogaritmisch papier.
Enkellogaritmisch papier.
De x-as van dit papier is "normaal" maar de schaalverdeling van de y-as is logaritmisch.
Wat heeft dat voor gevolgen?
Om de plaats van bijvoorbeeld het getal 200 op een logaritmische schaal te vinden moesten we de macht van 10 vinden.
10? = 200 geeft  ? = LOG200 = 2,3  en die 2,3 bepaalt de plaats van het getal 200.
Dat betekent dat op de y-as de afstand niet gelijk is aan y (zoals we gewend zijn op normaal papier) maar gelijk aan LOG y
Eigenlijk staat er dus niet y uitgezet, maar LOG y:

ypapier = LOG(y)

Neem iets simpels als de grafiek van y = x2 . Als je die op enkellogaritmisch papier gaat tekenen dan geeft dat precies dezelfde vorm als de grafiek van  ypapier = LOG y = LOG(x2) op gewoon papier. Kijk maar:

Het wordt pas interessant als we de grafieken van exponentiële functies op dit papier gaan tekenen.
Laten we voorspellen wat er zal gaan gebeuren.
Neem de functie  y = B •  gx
Op enkellogaritmisch papier zal dat worden  ypapier = LOG(y) = LOG(B • gx) = LOG(B) +  x • LOG(g)
Maar LOG(g) en LOG(B) zijn constanten, dus staat er  ypapier= a • x + b
Het wordt een rechte lijn!

Enkellogaritmisch papier maakt van exponentiële functies rechte lijnen

Het beginpunt van die lijn zal  (0, 10B) zijn, en de helling is LOG g.
Dat geeft natuurlijk een handige manier om te onderzoeken of een verband exponentieel is of niet: Teken de gevonden meetwaarden op enkellogaritmisch papier, en als er (ongeveer) een rechte lijn uitkomt dan is het verband (ongeveer) exponentieel.
   
OPGAVEN
1. Onderzoek of de volgende tabel een exponentieel verband beschrijft voor P als functie van q.
q 4,1 8,9 9,5 12,0 13,3
P 4,0 67,3 95,8 416,5 894,2
2. Eén van beide onderstaande tabellen beschrijft een exponentieel proces.
Laat met enkel-logaritmisch papier zien welke tabel dat is en geef een functievoorschrift voor de tabel die bij die exponentiële groei hoort.
   
 
x 5,4 8,0 1,2 9,8 4,6 2,8
y 7040 76300 165 397000 3380 650
   
 
x 28 10 16 32 40 52
y 6580 300 1230 9830 15000 18500
   
   
3. Welke hoek maakt de grafiek van   y = 3 • 2,5x  op enkellogaritmisch papier met de x-as?
Geef je antwoord zonder de lijn werkelijk te tekenen.

22º
4. De KNVB (Koninklijke Nederlandse Vegetariërs Bond)  heeft in de loop der jaren steeds meer leden gekregen. Voor een  bepaalde periode staan de ledenaantallen in de tabel hiernaast.
jaar aantal leden
1950
1951
1952
1953
1954
1955		 10000
10803
11666
12597
13605
14694
a. Bewijs dat de groei van het aantal leden (A) over deze periode exponentieel is. Stel een formule voor A(t) op en bereken daarmee wanneer er meer dan 100000 leden zullen zijn als deze groei zo doorgaat. Neem t = 0 in 1950.

t  ≈ 29,9
Ook de contributie (C) is in de loop der jaren gestegen. De gegevens daarvan staan in de volgende tabel.
jaar contributie
1950
1952
1954		 8,50
9,80
11,25
jaar contributie
1956
1958
1960		 12,95
14,85
17,10
b. Bewijs met enkellogaritmisch papier dat deze groei ook exponentieel is en geef een formule voor  C(t).
     
c. Het totale inkomen (I) van de penningmeester van de KNVB ten gevolge van alle contributie van alle leden is ook een exponentiële functie. Leg met de formules voor het ledenaantal en de contributie uit dat dat zo is, en bereken de groeifactor van dit totale inkomen.
   

g ≈ 1,156
d. Hoe ontstaat de grafiek van I(t)  op enkellogaritmisch papier uit de grafieken van A(t) en C(t)?
Leg duidelijk uit.
5.
Ik heb zojuist een erfenis van 8000 euro gekregen en wil het geld graag op een bankrekening zetten.
De bank geeft mij twee mogelijke spaarvormen:

1.  Spaarvorm A. 
Elke maand krijg ik, zolang het bedrag op mijn rekening minder dan 10000 euro is, een rente van 0,5%. Als het bedrag meer dan 10000 euro is wordt de rente verhoogd naar 2%

2. Spaarvorm B.
Ik krijg elke maand 1% rente, ongeacht het bedrag op mijn rekening. 
a. Geef een formule voor het bedrag bij spaarvorm A zolang dat kleiner is dan 10000 euro. Bereken vervolgens wanneer er 10000 euro op mijn rekening zal staan. Neem t in maanden met t = 0 op het moment dat ik het geld op de bank zet. 

t = 44,74
b. Teken de bedragen op de rekening volgens spaarvorm A en spaarvorm B in één figuur op enkellogaritmisch papier. Lees af wanneer beide spaarvormen een even groot bedrag op de rekening leveren.
c. Bereken het antwoord op vraag b) exact.

t = 68
d. Welk beginbedrag zou volgens spaarvorm A na 40 maanden een eindbedrag van 15000 euro opleveren?  Beantwoord je vraag met behulp van het logpapier en ook met een berekening.
     

t = 68
       
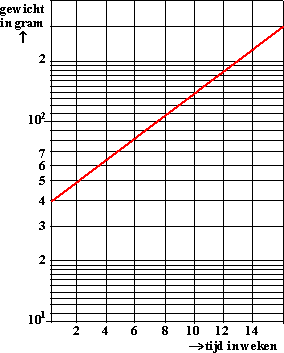
6. Een bloemenkweker verzorgt zijn bloemen goed. Hij plant regelmatig nieuwe bloemen, en houdt de gegevens daarvan vervolgens nauwkeurig bij. Dat leverde hem bijvoorbeeld voor zijn tulpen de grafiek hiernaast op enkellogaritmisch papier.
Op de x-as staat de tijd na planten in weken, op de y-as het gewicht van een bloem.
     
  a. Stel een vergelijking op voor het gewicht G als functie van de tijd t
   

G = 40 • 1,13t
  Voor het gewicht van narcissen hebben twee werknemers ook geprobeerd een vergelijking op te stellen.
Zij kwamen met het volgende resultaat:
werknemer I:   G(t) = 20 • 1,22t
werknemer II:  G(t) = 60 • 1,12t 
     
  b. Teken de bijbehorende grafieken in de figuur hiernaast.
       
  De narcissen worden geplukt om verkocht te worden bij een gewicht van 120 gram.
       
  c. Bepaal met de figuur hoeveel weken eerder dat volgens werknemer II gebeurt vergeleken met werknemer I. Geef vervolgens ook een exacte berekening van dit tijdsverschil..
     

2,895 weken
  d. Werknemer I ging bij het maken van zijn formule uit van een te laag begingewicht.
Hoe groot zou zijn begingewicht (bij een groeifactor van 1,22) moeten zijn als de narcissen volgens beide formules tegelijk geplukt kunnen worden? Onderzoek dat eerst met de figuur, geef vervolgens een berekening.
     

35,6 gram
   
7. Een zwangere vrouw laat elke week bij het consultatiebureau het gewicht en de lengte van het embryootje bepalen. Dat levert voor het gewicht tussen de tiende en de twintigste week de volgende gegevens: 
       
 
week 10 11 12 13 14 15 16 17 18 19 20
gewicht in gram 4 7 14 20 23 50 65 103 131 240 298
       
  Zet deze gegevens uit op enkellogaritmisch papier, laat zien dat er een exponentieel verband geldt en stel daar een formule voor op.
       
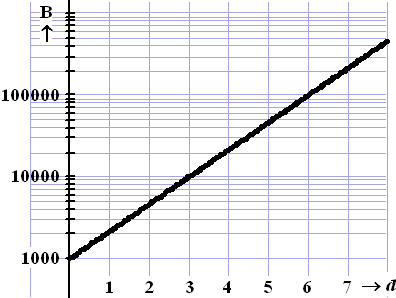
8. In een koelkast blijven eieren langer goed, want in eieren die niet koel bewaard worden groeien salmonella-bacteriën sneller. In de figuur hieronder staan de resultaten van een proef waarbij een ei werd bewaard in een koelkast die op 0ºC was afgesteld. Er werd bijgehouden hoe het aantal salmonella bacteriën (B) zich in de loop van de tijd ontwikkelde. Op de x-as staat het aantal dagen (d) vanaf het begin van de koeling. 
       
 

       
  Volgens de warenwet mogen er ten hoogste 2 miljoen bacteriën aanwezig zijn in een ei. Zijn er meer bacteriën aanwezig dan wordt het ei afgeleurd en mag het niet meer gegeten worden.
       
  a. Geef een formule voor B(d) en bereken of het ei na 10 dagen in de koelkast nog gegeten mag worden.
     

nee: 2154434
  Voor een ei dat in het begin 1000 salmonella bacteriën bevat en in een koelkast wordt gelegd blijkt de volgende formule te gelden:   log B = 1/3 • 1,32T • d + 3
Hierin is B het aantal bacteriën, T de koelkast-temperatuur in ºC en d het aantal dagen dat het ei in de koelkast ligt.
       
  b. Leg uit hoe het getal 3 uit de formule al volgt uit bovenstaande gegevens.
       
  c. Het ei blijkt bij een bepaalde temperatuur van de koelkast na precies 4 dagen koelen al 5 miljoen salmonella bacteriën te bevatten. Bereken dan in één decimaal nauwkeurig op welke temperatuur de koelkast staat afgesteld.
     

3,7 °C
  d. Uit bovenstaande formule is af te leiden dat bij elke waarde van T het verband tussen B en d exponentieel is. Neem aan dat de koelkast op 2ºC is afgesteld.
Geef dan de groeifactor van het exponentiële verband B(d). Geef je antwoord in twee decimalen nauwkeurig. 
     

3,81
       
9. In de Noordzee werden in 1992 twee aardgasvelden ontdekt die beiden de moeite van het exploiteren waard zijn.
De inhoud van de beide velden is 6 miljard m3 gas. In het begin levert zo'n gasveld veel gas, maar in de loop van de tijd wordt het steeds moeilijker er gas uit te winnen. Zolang dat meer dan 1 miljard m3 per jaar is, is het rendabel om het gas te winnen.

In 1995 begon met het exploiteren van het eerste gasveld. Voor de aanwezige hoeveelheid gas gold in de loop van de eerste paar jaren de volgende tabel:
       
 
gasinhoud veld I (in miljarden m3) 6,0 4,7 4,3 3,8 3,4 3,1
jaartal 1995 2001 2003 2006 2009 2011
       
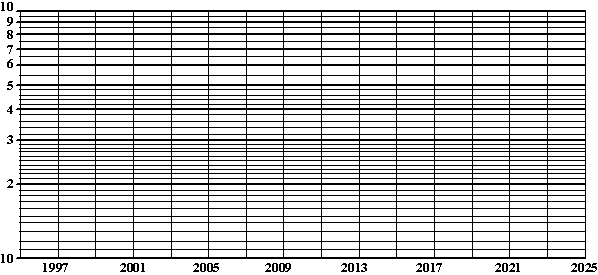
  a. Laat met een grafiek op het logpapier hieronder zien dat deze gashoeveelheid exponentieel verloopt.
       
 

       
  b. Bepaal met deze grafiek zo goed mogelijk hoe lang dit gasveld rendabel zal zijn.
     

2039
  Het tweede gasveld was pas in 2010 klaar om leeggehaald te gaan worden.
Door de intussen iets geavanceerdere apparatuur was men in staat uit dit veld jaarlijks 8% van de aanwezige hoeveelheid gas te winnen.
       
  c. Teken in je eerdere figuur ook de grafiek van de gashoeveelheid in dit tweede veld, en lees af wanneer beide velden even vol zullen zijn.
     

2023

© h.hofstede (h.hofstede@hogeland.nl)