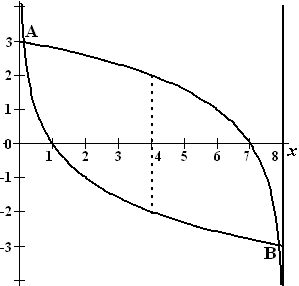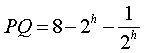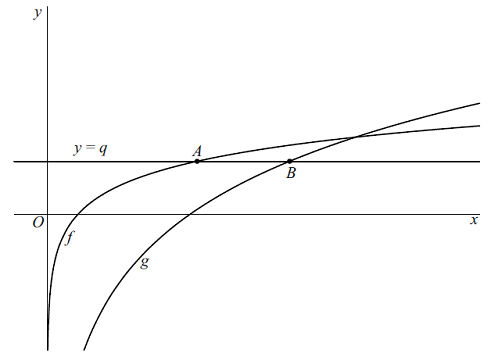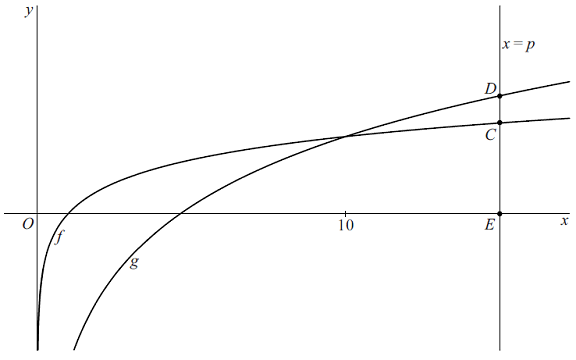Lijnstukken in grafieken.

© h.hofstede (h.hofstede@hogeland.nl)
   
Een algemene aanpak om lengtes van lijnstukken bij grafieken te berekenen staat in  les C9.

Doe die eerst.....

Je kunt de opgaven bij die les wel overslaan, en meteen de opgaven die hieronder staan gaan proberen.
Die opgaven zijn namelijk toegespitst op logaritmische en exponentiële functies.

Veel plezier ermee!
   
   
1. Gegeven zijn de functies  f(x) = 2log(x + 4)  en  g(x) = 5 - 2log x
       
  a. Schets de grafieken van f en g en los op:  f(x) ≤ g(x).
     

〈0, 4]
  b. De lijn x = p snijdt de grafieken van f en g in de punten A en B zodat AB = 2.
Bereken p op algebraïsche wijze.
     

-2 + 2√3
-2 + √132
  c. De lijn y = q snijdt de grafieken van f en g in de punten C en D zodat CD = 10.
Bereken q op algebraïsche wijze.
     

  q = 1,77 of 4
   
2. Gegeven zijn de functies  f(x) = 4x - 1  en  g(x) = 40 - 4x
       
  a. Schets de grafieken van f en g en los op:  f(x) ≤ g(x).
     

〈←, 2.5]
  b. De lijn x = p snijdt de grafieken van f en g in de punten A en B zodat AB = 30.
Bereken p op algebraïsche wijze.
     

p = 1,5 of 2,90
  c. De lijn y = q snijdt de grafieken van f en g in de punten C en D zodat CD = 1.
Bereken q op algebraïsche wijze.
Geef je antwoord in twee decimalen.
     

q = 20 of 2,35
       
3. Gegeven zijn de functies  f(x) = 0,5x - 2  en  g(x) = 5 - 0,5x
Maak voor het vervolg van deze opgave eerst een schets van de grafieken van f en g.
       
  a. De lijn y = q snijdt de y-as in punt A, de grafiek van f  in punt B en de grafiek van g in punt C.
Bereken algebraïsch q als gegeven is dat A het midden van BC is.
     

q = 1 of q = 2,5
  b. De lijn x = p  (p > 0) snijdt de x-as in punt P, de grafiek van f  in Q en de grafiek van g in R.
Bereken algebraïsch p als gegeven is dat PQ : QR = 4 : 35.
     

p = 3
       
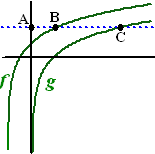
4. Gegeven zijn de functies
f(x) = 6log(x + 2) en  g(x) = 6log(x)-1/5
De grafieken staan hiernaast.

     
  De lijn y = q snijdt de y-as in punt A en de grafieken van f en g achtereenvolgens in de punten B en C.
Bereken algebraïsch q als geldt dat AB : BC = 3 : 2
Geef je antwoord in twee decimalen nauwkeurig.
   

q =1,48
       
5. Examenvraagstuk

Gegeven zijn de functies:  
f(x) = 2log (1/x)  en  g(x) = 2log(8 - x)

We nemen in dit vraagstuk alleen die waarden van x waarvoor f en g beiden betekenis hebben, 
dus 0 < x < 8. De grafieken snijden elkaar in de punten A en B.
     
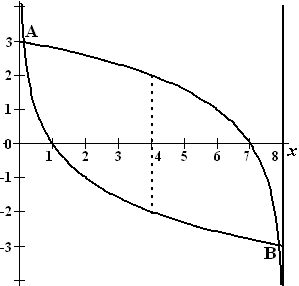  a. Bereken algebraïsch de coördinaten van A en B. Geef je antwoord in twee decimalen nauwkeurig.
   

(7.87,-2.98) en (0.13, 2.98)
  Bekijk alle verticale verbindingslijnstukken van de twee grafieken, voor zover die tussen A en B liggen. Bij  x = 4 is de lengte van het verbindingslijnstuk gelijk aan 4 (zie de figuur)
     
  b. Onderzoek of zo'n verticaal lijnstuk langer kan zijn dan 4.
   

NEE
 
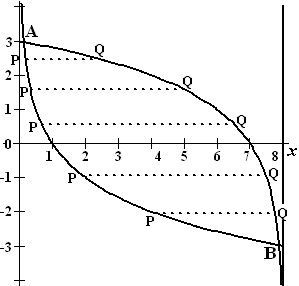
  PQ is een horizontaal verbindingslijnstuk. In de figuur hiernaast zijn een aantal zulke lijnstukken getekend. Bekijk een horizontaal lijnstuk op hoogte h ten opzichte van de x-as. De lengte PQ wordt gegeven door de formule:
 
 
     
  c. Toon aan dat deze formule correct is.
     
  d. Bereken algebraïsch de waarden van h waarvoor geldt dat
PQ = 5,5.
   

h = 1 of h = -1
       
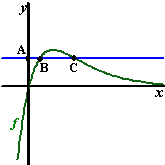
 6. Gegeven is de functie  f(x) = 2 • (1/3)x • x.

De lijn y = q snijdt de y-as in punt A en de grafiek van f in de punten B en C, zoals in de figuur hiernaast.

Bereken q als geldt dat AB : BC = 1 : 2.

   

p = 1/3√3
       
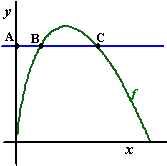
7. Gegeven is de functie f(x) = -4x • 2logx  met domein  〈0, 1]

De lijn y = q snijdt de y-as in punt A en de grafiek van f in de punten B en C, zoals in de figuur hiernaast.

Bereken q als geldt dat  AB : BC = 2 : 3
Geef je antwoord in 4 decimalen nauwkeurig.

   

q ≈ 1,9137
       
8. Gegeven zijn de functies  f(x) =  2log(x + 4)  en  g(x) = 8 - 2log x
       
  a. De grafieken snijden van de lijn x = a een lijnstuk af met lengte 3. Bereken a.
     

a = 4 of a ≈ 43,3
  b. De grafieken snijden van de lijn y = b een lijnstuk af met lengte 130. Bereken b.
     

b = 1 of b ≈ 7,09
       
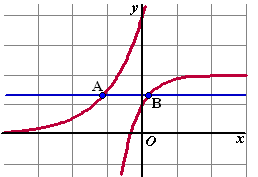
9. Hiernaast zie je de grafieken van y = 4ex  en  y = 2 - e-2x 
De lijn y = p snijdt de grafieken in de punten A en B.

     
  a. Toon aan dat xA = ln(p/4)
     
  b.

       
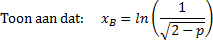  c. Toon aan dat voor de lengte L van AB geldt:  L = ln4 - lnp - 0,5ln(2 - p)
       
  d. Bereken algebraïsch de minimale lengte van AB in twee decimalen nauwkeurig..
     

1,30   (p = 4/3)
       
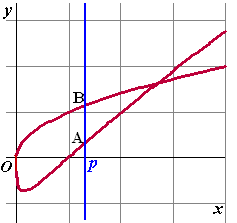
10. Hiernaast zie je de grafieken van y = √x • lnx  en y = √x
De lijn x = p (met p < 1) snijdt deze grafieken in de punten A en B.

Voor de lengte van lijnstuk AB geldt dan AB = √p(1 - lnp)

     
  a. Toon dat aan.
     
  b. Bereken voor welk p lijnstuk AB maximale lengte heeft.
   

p = e-1
  c. Bereken voor welke p driehoek OAB maximale oppervlakte heeft.
   

p = e1/3
 
       
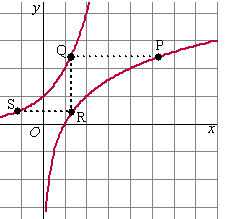
11. Hiernaast zie je in één figuur de grafieken van y = 2x  en  y = 2logx
Een punt P ligt op de grafiek van y = 2logx.
De lijn door P evenwijdig aan de x-as snijdt de grafiek van y = 2x in het punt Q.
De lijn door Q evenwijdig aan de y-as snijdt de grafiek van y = 2logx in punt R.
De lijn door R evenwijdig aan de x-as snijdt de grafiek van y = 2x  in punt S.

     
  a. Bereken de coördinaten van P als de y-coördinaat van R gelijk is aan 1.
   

(16, 4)
  b. Voor welke punten P bestaat er geen punt S?
   

xP ≤ 4
 
       
12. Examenopgave VWO,  Wiskunde B, 2019-II
       
 

De functies f en g worden gegeven door:

f (x) = log(√x)   en g(x) = log(x√x) - 1

De lijn met vergelijking y = q snijdt de grafiek van f  in het punt A en de grafiek van g in het punt B. Zie de figuur.
       
 

       
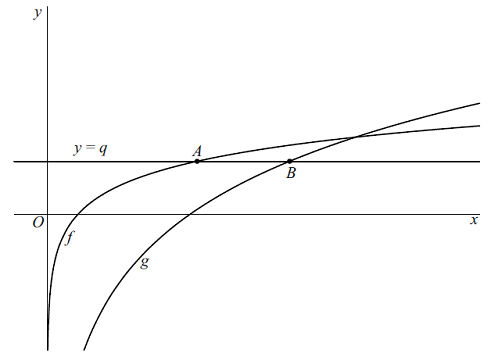  a. Voor welke q -waarden is AB = 3?
     

0,34 en -0,20
  Het snijpunt van de twee grafieken ligt bij x = 10.
Gegeven is p > 10. De lijn met vergelijking x = p ligt dan rechts van het snijpunt van de twee grafieken.
De lijn met vergelijking x = p snijdt de grafiek van f in het punt C, de grafiek van g in het punt D en de x-as in het punt E.
Doordat p > 10 , ligt D boven C. Zie onderstaande figuur.
       
 

       
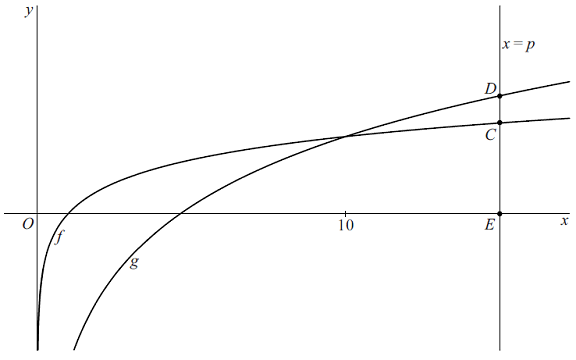  De verhouding tussen de lengte van lijnstuk CD en de lengte van lijnstuk CE hangt af van p.
Er geldt:  CD/CE = (2logp - 2)/logp
       
  b. Bewijs dat deze formule voor CD/CE  juist is.
       
  Als p onbegrensd toeneemt, nadert de verhouding CD/CE tot een grenswaarde.
       
  c. Bereken exact deze grenswaarde.
     

 2 

13. Examenopgave HAVO,  Wiskunde B, 2021-III

De functies f en g worden gegeven door

    f(x) = log(2x - 4)
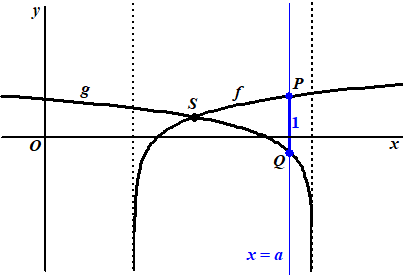
g(x) = log(6 - x)
       
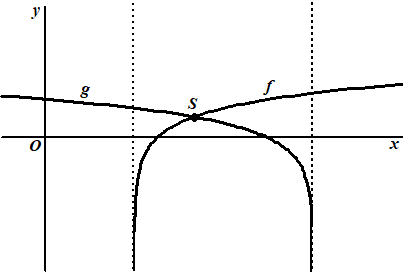
  Beide grafieken hebben een verticale asymptoot. Het punt S is het snijpunt van de grafieken van f en g. Zie de figuur.
       
 

       
  De afstand van S tot de asymptoot van de grafiek van g is groter dan de afstand van S tot de asymptoot van de grafiek van f.
       
  a. Bereken exact hoeveel keer zo groot.
     

 twee keer 

  De lijn met vergelijking x = a ligt rechts van S en snijdt de grafieken van f en g in de punten P en Q.
De waarde van a is zo gekozen dat de lengte van lijnstuk PQ gelijk is aan 1. Zie onderstaande figuur.
       
 

       
  b. Bereken exact de waarde van a.
     

 51/3 

     

© h.hofstede (h.hofstede@hogeland.nl)