Nieuwe pagina 1

© h.hofstede (h.hofstede@hogeland.nl)

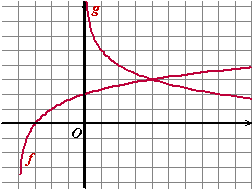
Zie de figuur hiernaast.

²log(x + 4) = 5 - ²logx
²log(x + 4) + ²logx = 5
²log(x(x + 4)) = 5
x(x + 4) = 2⁵ = 32
x² + 4x - 32 = 0
(x - 4)(x + 8) = 0
x = 4 ∨ x = -8
Alleen x = 4 voldoet.

f(x) ≤ g(x) geldt dan voor 〈0, 4] (zie de figuur)

x = p geeft f(x) = ²log(p + 4) en g(x) = 5 - ²logp

Voor 0 < p < 4 is g > f
Dan is AB = 5 -²logp -²log(p + 4) = 2
3 = ²logp +²log(p + 4)
3 =²log(p(p + 4))
8 = p(p + 4)
p² + 4p - 8 = 0
p = ^{(-4 ±
√(16 + 32))}/₂
p = ^{(-4 ±
√48)}/₂
p = -2 ± 2√3 en de waarde tussen 0 en 4 is p = -2 + 2√3

Voor p > 4 is f > g
Dan is AB = ²log(p + 4) - 5 + ²logp = 2
7 = ²log p(p + 4)
p(p + 4) = 2⁷ = 128
p² + 4p - 128 = 0
p = ^{(-4 ±
√(16 + 512))}/₂
p = ^{(-4 ±
√528)}/₂p = -2 ± √132 en de waarde groter dan 4 is p = -2 + √132

Stel dat de snijpunten van y = q met de grafieken van f en g liggen bij x = p en x = p + 10

Voor q > 3 geldt : g(p) = f(p + 10)
5 - ²logp = ²log(p + 10 + 4)
5 = ²log(p + 14) + ²logp
5 = ²log(p(p + 14))
32 = p² + 14p
p² + 14p - 32 = 0
p = ^{(-14 ±
√(196 + 128))}/₂
p = ^{(-14 ±
√324)}/₂
p = 2 ∨ p = -16
de gezochte oplossing is p = 2 en dat geeft q = 5 - ²log2 = 4

Voor q < 3 geldt f(p) = g(p + 10)
²log(p + 4) = 5 -²log(p + 10)²log(p + 4) +²log(p + 10) = 5
²log((p + 4)(p + 10)) = 5
(p + 4)(p + 10) = 32
p² + 14p + 8 = 0
p = ^{(-14 ±
√(196 - 32))}/₂
p = ^{(-14 ±
√164)}/₂
p = -7 ± √41
De gezochte oplossing is p = -7 + √41 (≈ -0,6)
Dat geeft q = f(p) = ²log(p + 4) ≈ 1,77

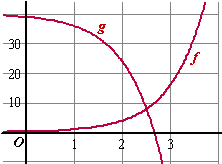
Zie hiernaast

f = g
4^{x - 1} = 40 - 4^x4^x • 4^-1 = 40 - 4^x
0,25 • 4^x= 40 - 4^x1,25 • 4^x = 40
4^x = 32
(2²)^x = 2⁵2^2x = 2⁵
2x = 5
x = 2,5

f ≤ g geldt dan voor x in 〈←, 2.5]

x = p geeft f(x) = 4^{p - 1} en g(x) = 40 - 4^p

Voor p < 2,5:
AB = 30 = 40 - 4^{p -}4^{p - 1}
4^p + 4^{p - 1} = 10
4^p + 0,25 • 4^p = 10
1,25 • 4^p = 10
4^p = 8
(2²)^p = 2³2^2p = 2³
2p = 3
p = 1,5

Voor p > 2,5:
AB = 30 = 4^{p - 1} - 40 + 4^p
70 = 4^{p - 1} + 4^p
70 = 0,25 • 4^p + 4^p
70 = 1,25 • 4^p
4^p = 56
p = ⁴log56(≈ 2,90)

Twee mogelijkheden:

f(p) = g(p + 1)
4^{p - 1} = 40 - 4^p+1
0,25 • 4^p + 4 • 4^p = 40
4,25 • 4^p = 40
4^p = 9,411
p = ⁴log9,411 = 1,62
Dan is q = f(p) = 4^{p - 1} = 2,35

g(p) = f(p + 1)
40 - 4^p = 4^p
4^p= 20
p = ⁴log20
q = g(p) = 40 - 20 = 20

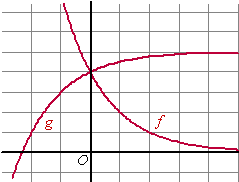
Als A het midden van BC is, dan moet gelden;
f(p) = g(-p)
0,5^{p - 2} = 5 - 0,5^-p
0,5^p • 0,5^-2 = 5 - (0,5^p)^-1
noem 0,5^p= a
Dat geeft 4a = 5 - 1/a
4a² = 5a - 1
4a² - 5a + 1 = 0
a = ^{(5 ±
√(25-16))}/₈ = ^{(5
± 3)}/₈ = 1 of ¹/₄.

a = 1 geeft 0,5^p = 1 ⇒ p = 0 en dat is de flauwe oplossing A = B = C en q = 4

a = ¹/₄ geeft 0,5^p = ¹/₄ ⇒ p = 2

Dan is q = f(2) = 0,5^2-2 = 1

PQ = f(p) = 0,5^{p - 2}
PR = g(p) = 5 - 0,5^p
Als PQ : QR = 4 : 35 dan is PQ = ⁴/₃₉ • PR ofwel 39 • PQ = 4 • PR
39 • 0,5^{p - 2} = 4 • (5 - 0,5^p)
39 • 0,5^p • 0,5^-2 = 20 - 4 • 0,5^p
156 • 0,5^p + 4 • 0,5^p = 20
160 • 0,5^p = 20
0,5^p = ¹/₈
0,5^p = 0,5³p = 3

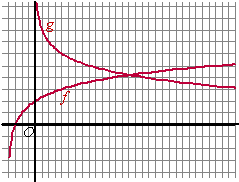
Als AB = 3p dan is AC = 5p
Dus moet gelden f(3p) = g(5p)
⁶log(3p + 2) = ⁶log(5p) - ¹/₅
⁶log(5p) -⁶log(3p + 2) = ¹/₅⁶log(^5p/_{(3p + 2)}) = ¹/₅^5p/_{(3p + 2)} = 6^1/5 =1,435p= 1,43 • (3p + 2)
5p = 4,29p + 2,86
0,71p = 2,86
p = 4,05
Dan is q = f(3p) = 1,48

²log (¹/_x) = ²log(8 - x)
¹/_x = 8 - x
1 = 8x - x²
x² - 8x + 1 = 0
x = ^{(8 ±
√(64 - 4))}/₂ = 7,87 of 0,13
x = 7,87 geeft y = -2,98
x = 0,13 geeft y = 2,98

De lengte van zo'n lijnstuk is L = ²log(8 - x) -²log(1/x) L =²log((8 - x) • x) = ²log(8x - x²)
²logx is maximaal als x maximaal is.
in dit geval moet 8x - x² maximaal zijn en dat is bij de top van deze parabool, dus bij x = ^-8/_-2 = 4
een langer lijnstuk is dus NIET mogelijk.

y = h geeft met de grafiek van f(x) het snijpunt bij ²log(¹/_x) = h
¹/_x = 2^h ⇒ x_P = ¹/₂h

y = h geeft met de grafiek van x het snijpunt bij²log(8 - x) = h8 - x = 2^h ⇒ x_Q = 8 - 2^h De afstand PQ = x_Q - x_P = 8 - 2^h - ¹/₂h

5,5 = 8 - 2^h - ¹/₂h
Noem 2^h = a
Dan staat er 5,5 = 8 - a - ¹/_a
5,5a = 8a - a² - 1
a² - 2,5a + 1 = 0
(a - 0,5)(a - 2) = 0
a = 0,5 ∨ a = 2
2^h = 0,5 ∨ 2^h = 2
h = -1 ∨ h = 1

Stel x_B = p
Dan moet gelden: x_C = 3p dus is f(p) = f(3p)
2 • (¹/₃)^p • p = 2 • (¹/₃)^3p • 3p
2 • (¹/₃)^p = 6 • (¹/₃)^3p
(1/3)^-2p = ⁶/₂ = 3
-2p = -1
p = ¹/₂
q = f(p) = 2 • (¹/₃)^0,5 • 0,5 = √(¹/₃)

Stel x_B = 2p dan is x_C = 5p
Dan moet gelden f(2p) = f(5p)
-4 • 2p • ²log2p = -4 • 5p • ²log5p
2 •²log2p = 5 •²log5p
²log(2p)² =²log(5p)⁵ ⁽2p)² =(5p)⁵ 4p² = 3125p⁵ 4p² - 3125p⁵ = 0p² (4 - 3125p³) = 0p = 0 ∨ 4 = 3125p³
p = 0 ∨ p = (⁴/₃₁₂₅)^1/3 = 0,1086
p = 0,1086 geeft q = f(2p) = -4 • 2p • ²log2p = 1,9137

x = a geeft y_f = ²log(a + 4) en y_g = 8 - ²logaDe afstand is y_f - y_g of y_g - y_f.

y_f - y_g = 3
²log(a + 4) - 8 + ²loga = 3
²log((a + 4)a) = 11
(a + 4)a = 2¹¹ = 2048
a² + 4a - 2048 = 0 de ABC-formule geeft a = 43,3 ∨ a = -47,3
De oplossing die voldoet is a = 43,3

y_g - y_f.= 3
8 - ²loga-²log(a + 4) = 3
5 = ²loga + ²log(a + 4)
5 = ²log(a(a + 4))
2⁵ = 32 = a(a + 4)
a² + 4a - 32 = 0
de ABC-formule geeft dan a = 4 ∨ a = -8
De oplossing die voldoet is a = 4

Er moet gelden f(p) = g(p + 130) of g(p) = f(p + 130)

f(p) = g(p + 130)
²log(p + 4) = 8 -²log(p + 130)²log(p + 4) +²log(p + 130) = 8
²log((p + 4)(p + 130)) = 8
(p + 4)(p + 130) = 2⁸ = 256
p² + 134p + 264 = 0
De ABC-formule geeft dan p = -2 ∨ p = -132 De oplossing die voldoet is p = -2
Dan is b = f(p) = ²log(-2 + 4) = 1

g(p) = f(p + 130)
8 - ²logp = ²log(p + 134)
8 = ²logp + ²log(p + 134)
8 = ²log(p(p + 134))
2⁸ = 256 = p(p + 134)
p² + 134p - 256 = 0
De ABC-formule geeft dan p = 1,88 ∨ p = -135,88
De oplossing die voldoet is p = 1,88
Dan is b = g(p) = 8 - ²log(1,88) = 7,09

4e^x = p
e^x = ^p/₄
x = ln(^p/₄)

2 - e^-2x = p
e^-2x = 2 - p
-2x = ln(2 - p)
x = -¹/₂ln(2 - p)
x = ln(2 - p)^-0,5
x = ln(¹/_{√(2 - p)})

De lengte van AB is L = x_B - x_A = -¹/₂ln(2 - p) - ln(^p/₄)
L = -0,5ln(2 - p) - (ln(p) - ln4)
L = -0,5ln(2 - p) - lnp + ln4

De lengte is minimaal als de afgeleide nul is.
L ' = -0,5 • ¹/_{(2 - p)} • -1 - ¹/_p = 0
^0,5/_{(2 - p)} = ¹/_p
0,5p = 2 - p
1,5p = 2
p = ⁴/₃
Dan is L = -0,5ln(2 - ⁴/₃) - ln⁴/₃ + ln4 = 1,30

10.

x = p geeft y_A = √p • lnp en y_B = √p
Dan is AB = y_B - y_A = √p - √p • lnp = √p (1 - lnp)

AB is maximaal als de afgeleide nul is:
¹/_2√p• (1 - lnp) + √p • -¹/_p = 0
¹/_(2√p) • (1 - lnp) = ^√^p/_p = ¹/_√p
1 - lnp = 2
lnp = -1
p = e^-1

De oppervlakte van driehoek OAB is 0,5 • p • AB = 0,5p√p (1 - lnp) = 0,5p^1,5•(1 - lnp)
De oppervlakte is maximaal als de afgeleide ervan nul is;
1,5 • 0,5 • p^0,5 • (1 - lnp) + 0,5p^1,5 • -¹/_p = 0
0,75p^0,5(1 - lnp) = 0,5p^0,5
0,75(1 - lnp) = 0,5
1 - lnp = ²/₃
lnp = ¹/₃
p = e^1/3

11.

y_R = 1
²logx_R = 1
x_R = 2
x_Q = 2
y_Q = 2² = 4
y_P = 4
²logx_P = 4
x_P = 2⁴ = 16 dus P = (16, 4)

Punt S bestaat niet als y_S ≤ 0
y_S = 0 geeft y_R = 0
²logx_R = 0
x_R = 1
x_Q = 1
y_Q = 2¹ = 2
y_P = 2
²logx_P = 2
x_P = 2² = 4
Als x_P ≤ 4 dan bestaat punt S niet.

12.

Stel x_A = p, dan is x_B = p + 3
Die moeten dezelfde y opleveren
Dus log(√p) = log(p + 3)√(p + 3)) - 1
Y1 = log(√X)
Y2 = log((X + 3)√(X + 3)) - 1
intersect geeft twee snijpunten:
X = 4,8648... en Y = q = 0,34
X = 0,38936... en Y = q = -0,20

DE = log(p√p) - 1
CE = log(√p)
CD = DE - CE = log(p√p) - 1 - log(√p)
CD = log(p√p) - log10 - log(√p)
CD = log(^p√p/₁_√_p) - 1 = log(p) - 1
CE = log(p^0,5) = 0,5logp

CD/CE = ^{(logp
- 1})/_0,5logp = ^{(2logp - 2)}/_logp

Deel teller en noemer door log(p):

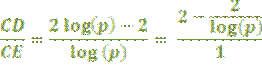als log(p) naar oneindig gaat, gaat ²/_log(p) naar nul.
Dan gaat de breuk naar ²/₁ = 2

13.

Een log-grafiek heeft een verticale asymptoot bij log(0)
verticale asymptoot van f: 2x - 4 = 0 dus x = 2
verticale asymptoot van g: 6 - x = 0 dus x = 6

snijpunt f en g:
log(2x - 4) = log(6 - x)
2x - 4 = 6 - x
3x = 10
x = 3¹/₃

de afstanden van S tot de asymptoten zijn ⁴/₃ en ⁸/₃
De afstand van S naar de asymptoot van g is dus twee keer zo groot als van S naar de asymptoot van f

Als de verticale afstand 1 is, dan is f(p) - g(p) = 1
log(2x - 4) - log(6 - x) = 1
log(^{(2x - 4)}/_{(6 - x)}) = 1
(2x - 4)/(6 - x) = 10¹ = 10
2x - 4 = 10(6 - x)
2x - 4 = 60 - 10x
12x = 64
x = 5¹/₃ = a