| |
 |
| Breuken. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Het is eigenlijk allemaal heel
eenvoudig met die algebra: als je weet hoe het met getallen moet, dan
doe je het met letters gewoon precies zo!
Gewoon na-apen!
We zullen drie bewerkingen met breuken gaan bekijken, en elke keer
wat er gebeurt met getallen precies nadoen met letters. Die bewerkingen
zijn vermenigvuldigen, optellen, en vereenvoudigen.
|
 |
| 1.
Vermenigvuldigen van breuken. |
|
|
| Op de basisschool was het
simpel: als je breuken vermenigvuldigt moet je doen "teller
× teller en noemer × noemer". |
|
|
|
vermenigvuldigen:
teller × teller
noemer × noemer
|
|
|
|
Dat betekent bijvoorbeeld dat:
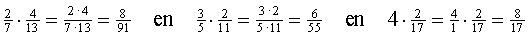
Nou, laten we dat dan ook maar precies zo met letters doen:
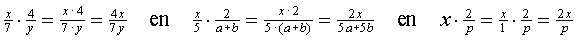
Vooral die laatste is interessant; daar zie je dat een
"gewone" letter in een blokje waar ook breuken in staan
eigenlijk hoort bij de teller van die breuken. Dat kun je snappen door
er "éénde" van te maken, en dan komt dat gewone getal dus
bij de teller terecht. Net zoals 5 • 2/7
= 10/7 is ook 4 • 2/x
= 8/x en 8 • x/3
= 8x/3 |
| |
|
|
Een gewoon getal is eigenlijk een
TELLER (de noemer is 1) |
|
| |
|
|
Dat zul je vooral vaak gebruiken als er ergens breuken tussen
haakjes staan. Hier zie je een voorbeeld met onze
"blokjesmethode". We bekijken de uitdrukking 5 •
(x + 6/x). Let op dat die 5 daar
voor de haakjes bij die teller 6 terecht komt!!! |
|
|
|
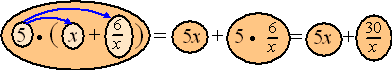
|
|
|
| 1. |
Schrijf zonder haakjes, en
vereenvoudig zoveel mogelijk: |
|
|
|
|
|
|
|
a. |
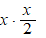
|
|
d. |
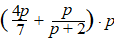
|
|
|
b. |
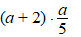
|
|
e. |
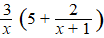
|
|
|
c. |
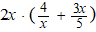
|
|
f. |
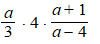
|
|
|
|
|
|
|
|
|
|
|
| 2.
Vereenvoudigen van breuken. |
|
|
Kijk naar het plaatje hiernaast.
Het illustreert wat er het vaakst fout gaat met het vereenvoudigen van
breuken. Dat is
|
|
De ziekte van het
"wegstrepen"!! |
|
|
Wegstrepen is ook helemaal niet het juiste woord voor wat er gebeurt
bij het vereenvoudigen van breuken. Hier staat hoe een breuk eigenlijk
wordt vereenvoudigd:
|
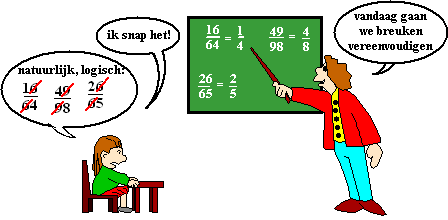 |
| In de tweede stap blijkt dat zowel in de teller als in de noemer
"keer 16" staat. In de derde stap zie je dat je die "keer
16" en "keer 16" bij elkaar mag zetten.
Maar
dat mag alléén omdat het vermenigvuldigen is!!!!
In de laatste stap is tenslotte gebruikt dat "keer 16" in de
teller en "keer 16" in de noemer elkaar opheffen.
Drie afgrijselijke fouten die met breuken en letters gemaakt worden: |
|
|
|
|
| Soms kun je door te ontbinden in
factoren er zelf voor zorgen dat er blokjes KEER elkaar komen te staan.
De volgende voorbeeldjes zullen dat hopelijk duidelijk maken. |
|
|
| voorbeeld 1.
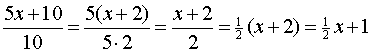
|
|
|
voorbeeld 2.
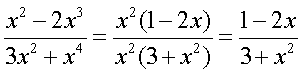 |
|
|
| 2. |
Vereenvoudig zo veel mogelijk: |
|
|
|
|
|
|
|
|
a. |
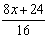
|
|
d. |
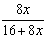
|
|
|
b. |
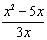
|
|
e. |
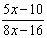
|
|
|
c. |
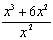
|
|
f. |
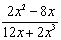
|
|
|
|
|
|
|
|
|
|
| |
|
Waarschuwing: Kijk uit met
letters wegstrepen!
Het gevaar van het wegstrepen
van letters is, dat je niet door nul mag delen. |
| |
|
|
|
| 3.
Optellen van breuken. |
|
|
| Op de basisschool heb je
waarschijnlijk al geleerd dat je breuken die je wilt optellen (of
aftrekken) eerst gelijknamig moet maken. Dat betekent dat je de noemers
gelijk moet maken, en dat kun je doen door teller en noemer van een breuk
op een handige manier met het zelfde getal te vermenigvuldigen.
Met getallen gaat het zó:
|
| |
|
|
 |
| |
|
|
En, dat zul je intussen al wel door hebben, met letters gaat het precies
hetzelfde!
Kijk maar, links met getallen, rechts met formules:
|
| |
|
|
 |
| |
|
|
En
ook breuken en "gewone"getallen kun je bij elkaar optellen,
als je maar bedenkt dan zo'n gewoon getal eigenlijk ook een breuk is,
maar met noemer 1. Dat zagen we hierboven trouwens ook al bij het
vermenigvuldigen van breuken.
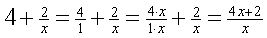
|
| |
|
|
|
|
|
| |
|
|
4.
Mintekens bij breuken. |
| |
|
Als er ergens in een breuk een
minteken staat, dan doet het er niet veel toe of dat in de teller of in
de noemer is.
Deze breuken zijn alle drie gelijk: |
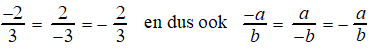 |
| |
|
De fouten worden meestal gemaakt
als er nog méér in de teller of de noemer staat.
Ik hoop dat je ziet dat dit verkeerd is: |
|
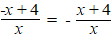 |
OEIOEIOEIOEI!!!!!!
Dat moet natuurlijk zó: |
|
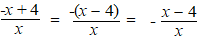 |
|
|
| |
 |
| |
|
|
 |
|
 |
|
|
|
|
| |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|