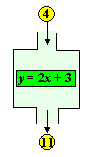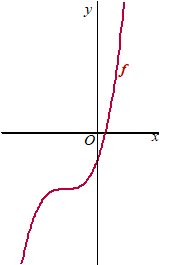De Inverse Functie.

© h.hofstede (h.hofstede@hogeland.nl)


functiebegrip
Een functie zagen we als een apparaat waar je een getal in kunt gooien, en waar na een tijdje een nieuw getal uit komt rollen. Zoals het  machientje hiernaast.
Wat we er allemaal in mochten gooien dat heette het DOMEIN, en wat er allemaal uit kon komen rollen dat heette het BEREIK.

Nou kun je zulke functies ook koppelen; dat is wel geinig. Je zet twee zulke machientjes onder elkaar zodat de uitvoer van de eerste weer de invoer van de tweede wordt.
Hieronder is dat voor een paar zulke machientjes gebeurd.

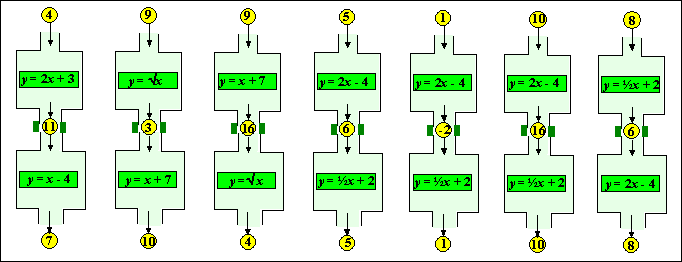
Aan de tweede en de derde zie je dat het wel degelijk verschil maakt in welke volgorde je de functies onder elkaar zet (de ene keer komt er 10 uit, de andere keer 4).
De laatste vier zijn apart:   wat je er ingooit, dat komt er ook weer uit!!!
Probeer er zelf nog maar een paar x-en in te gooien; het is echt altijd zo.

Kennelijk doet het tweede machientje al het werk van het eerste weer teniet! Je zou het de "OPHEFFER" of "OMGEKEERDE" van de eerste kunnen noemen. In de laatste twee figuren zie je dat het andersom óók werkt. Kennelijk zijn die twee machientjes elkáárs opheffer!!!!
Wiskundigen noemen zoiets niet een "opheffer"  maar een INVERSE.

HOE VIND JE ZO'N INVERSE?

Methode 1.   Door alles gewoon om te keren.

Kijk bijvoorbeeld hoe een wiskundeles in z'n werk gaat:

Maar aan het eind van de les moet je, als je dit allemaal wilt "opheffen" niet gewoon van alles het omgekeerde doen, dat geeft onzin. Kijk maar, hier staat van alles het omgekeerd, probeer dit maar eens te doen:

Het werkt pas als je van alles het omgekeerde doet, maar OOK IN DE OMGEKEERDE VOLGORDE!!!
Zó gaat het goed:

En dat werkt bij functies ook zo. Neem bijvoorbeeld het machientje  y = 2x + 8.
Wat doet dat met een getal x?  Eerst "KEER TWEE" en daarna "PLUS ACHT"
Omdat op te heffen moet je het omgekeerde doen in de omgekeerde volgorde:  eerst "MIN ACHT" en daarna "GEDEELD DOOR TWEE".  De inverse wordt dus  y = (x - 8)/2
       
Methode 2.  Door x en y met elkaar te verwisselen.
 
Als je dat gedoe met die machientjes maar vervelend vindt, dan kun je de inverse ook op een meer algebraïsche manier vinden. Kijk, als een functie bij elke x die je erin stopt een y produceert, dan maakt de inverse functie van die y weer de oorspronkelijke x. De inverse gebruikt die y eigenlijk alsof het een x is.
Daarom kun je een inverse functie makkelijk opsporen door gewoon x en y in de gegeven functie met elkaar te verwisselen, en dan het resultaat weer te gaan schrijven als y = .......
 
inverse opstellen:
•  vervang x door y en vervang  y door x
•  schrijf het resultaat als y = ....
 
       
Voorbeeld:  Geef de inverse functie van  y = 2/(x - 1) 
x en y verwisselen geeft  x = 2/(y - 1)
Dat geeft:   x = 2/(y - 1)  ⇒  x(y - 1) = 2  ⇒  xy - x = 2  ⇒  xy = 2 + x  ⇒  y = (2 + x)/x    (of ook wel y = 1 + 2/x)
En dat is de inverse.....

Voorbeeld:  Geef de inverse van   y = (2x - 1)/(5 - x)
x en y verwisselen geeft  x = (2y - 1)/(5 - y)
Dat geeft:  (5 - y)x = 2y - 1  ⇒  5x - yx = 2y - 1 ⇒  -yx - 2y = -1 - 5x 
⇒  y(-x - 2)  = -1 - 5x  ⇒  y = (-1 - 5x)/(-x - 2) = (1 + 5x)/(x + 2)

Je merkt dat je wel handig moet zijn met vergelijkingen veranderen. Daar kun je in  deze les meer over vinden.

Merk verder op dat dit tweede voorbeeld eigenlijk niet te doen is met methode 1, door alles om te keren.  Dat is te lastig met twee x-en erin.....

Kan dit zomaar altijd?

Gezien deze vraag waarschijnlijk niet, zul je wel denken. En dat klopt!

Dat zit hem in het volgende.

Onze afspraak was ooit, dat bij een functie er bij elke waarde van x hoogstens één y hoort.
Maar omdat een inverse functie eigenlijk x en y wisselt, moet er nu ook gelden dat er bij elke waarde van y hoogstens één x hoort. Als dat niet zo is, dan zou de inverse functie geen functie zijn!

Je kunt zien of dat zo is met de horizontale-lijn test.  Als elke horizontale lijn hoogstens één snijpunt met de grafiek van f  heeft, dan bestaat er bij elke y dus ook hoogstens één x, en dan bestaat de inverse functie.
Zo'n functie waarvoor dat geldt heet ook wel een één-op-één functie.
       

       
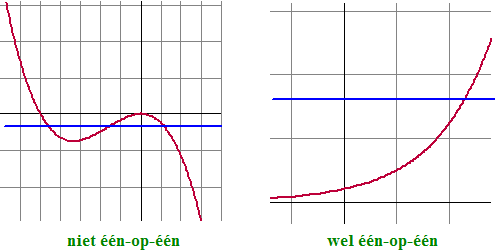
Die blauwe lijn in de linkergrafiek bederft de boel:  deze functie heeft geen inverse functie. Hier horen bij één y  meerdere x-en dus zou bij de inverse functie bij één x meerdere y-en horen, en dat mag niet bij een functie.
In de rechtergrafiek is alles in orde.
 
1.  Geef de inverse van de volgende functies:
a.     y =  4x - 5 d.  y = √(x + 2)
b.    y =  1 + 2/x e. y = 1 + 2√x
c.    y =  3 + 1/(x - 2)  f. y =  2(x + 3) + 4
2. Een functie heeft domein  [0,3].  Wat zegt dat over zijn inverse?
3. Graddus is op zoek naar de inverse van y = x2 . Hij heeft een vermoeden dat het y = √x is.  
Ter controle:   x = 4 geeft  x2 = 16  en   x = 16 geeft inderdaad weer √16 = 4
Het lijkt te kloppen!!
a. Toch zijn er getallen waarvoor het vermoeden van Graddus niet klopt! Welke zijn dat?
b. De inverse van y = x2  bestaat eigenlijk uit twee functies. Welke zijn dat?
         
4. Geef de inverse van de volgende functies:
         
  a. y =  (x - 4)/(1 - 3x)    
  b. y = √(1 + 2/x)    
  c. y =  2x/(x - 8)    
         
5. Examenvraagstuk VWO Wiskunde B, 2022-I

De functies fp  en gp zijn gegeven door:
 
  Bewijs dat de functies  fp  en gp elkaars inverse zijn.
         
WAT HEBBEN DE GRAFIEKEN VAN INVERSEN MET ELKAAR TE MAKEN?
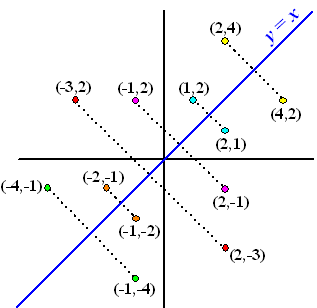
Dat is eenvoudig te zien door je te bedenken dat de inverse eigenlijk precies de x en y van de oorspronkelijke functie omwisselt. Als bijvoorbeeld op de oorspronkelijke functie het punt (2, 4) ligt dan heeft dat machientje van x = 2 een y = 4 gemaakt, dus dan zal de inverse van x = 4 weer een y = 2 maken. Het punt (4, 2) zal dan op de grafiek van de inverse liggen. Hieronder zie je een aantal punten en de bijbehorende punten op de inverse.
Het patroon zal duidelijk zijn: twee bij elkaar horende punten zijn steeds elkaars gespiegelde in de blauwe lijn, en dat is de lijn y = x:

Een functie en zijn inverse zijn elkaars gespiegelde
in de lijn y = x.

6. Kun je functies verzinnen die gelijk zijn aan hun eigen inverse?
7. Schets de grafieken van de inversen van de volgende functies:

8. a.  Een functie heeft een verticale asymptoot x = 4.  Wat zegt dat over zijn inverse?
b.  Een functie heeft een nulpunt x = -3. wat zegt dat over zijn inverse?
c.  Leg uit waarom een functie met een maximum of minimum geen inverse op het hele domein heeft.
9. De functie y = 2x + b snijdt zijn inverse bij  x = 5.  Bereken b.
   
10. Examenopgave VWO, Wiskunde B, 2016-II.

De functie f wordt gegeven door f (x) = (x + 1)3 − 1. In de figuur is de grafiek van f weergegeven.

 
  De functie g is de inverse functie van f.
   
  a. Bewijs dat g inderdaad de inverse functie is van f.
   
  De grafieken van f en g hebben gemeenschappelijke punten.
   
  b. Bereken exact de coördinaten van deze punten.
     
   
 

© h.hofstede (h.hofstede@hogeland.nl)