| |
|
|
|
|
| 1. |
De kromme K wordt gegeven door x(t)
= t5 - 4t3 en
y(t) = t2 |
| |
|
|
|
|
| |
a. |
Geef een vergelijking van de
raaklijn aan K in het punt waar t = 1 |
| |
|
|
|
|
| |
b. |
Leg uit waarom de vergelijkingen van
de raaklijnen aan K in het punt (0,0) niet te berekenen zijn met
de formule die je hebt geleerd voor de helling van een
parameterkromme. |
| |
|
|
| |
c. |
Geef een vergelijking van de beide
raaklijnen aan K in het andere snijpunt van K met
de y-as. Leg uit hoe het kan dat een parameterkromme twee
raaklijnen in één punt heeft. |
| |
|
|
|
|
| 2. |
De kromme K wordt gegeven door x(t)
= t3 - 4t en
y(t) = tet - et |
|
| |
|
|
|
|
| |
Geef een vergelijking van de
raaklijn aan kromme K in het snijpunt met de positieve y-as. |
| |
|
|
|
|
| |
|
|
| 3. |
De kromme K wordt gegeven door x(t)
= t2 - 2t en
y(t) = lnt
Voor welke b raakt de lijn y =
1/4x
+ b de kromme K? |
| |
|
|
|
|
| |
|
|
|
|
| 4. |
De parametervoorstelling van een
cirkel met middelpunt O en straal 1 is x(t)
= cost en y(t) = sint
Toon aan dat voor een willekeurig punt P van deze cirkel
geldt dat de lijn OP loodrecht staat op de raaklijn in P aan de
cirkel. |
| |
|
|
|
|
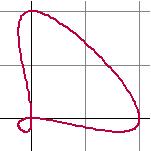
| 5. |
De kromme K wordt gegeven door
x(t)
= cos2t + cost en
y(t) = sin2t + sint
Geef een vergelijking van de raaklijn in het punt waar t
= 1/3π. |
 |
| |
|
|
|
|
| 6. |
examenvraagstuk Wiskunde,VWO,
1984. |
| |
|
|
|
|
| |
Ten opzichte van
een rechthoekig assenstelsel Oxy is de kromme K gegeven door:
x = -t2 + 6t en y
= -1/3t3
+ 2t2 waarbij t
∈ R |
| |
|
|
|
|
| |
a. |
Bereken de coördinaten van de
punten van K waarin de raaklijn aan K evenwijdig is aan de x-as
of aan de y-as. |
| |
|
|
|
|
| |
b. |
Toon aan dat er twee lijnen zijn
die K in O raken.
Bereken de hoek van deze lijnen in graden nauwkeurig.
Teken K. |
| |
|
|
| |
c. |
Voor welke p
∈ R+ geldt: de lijn
y = 2x - p raakt K ? |
| |
|
|
|
|
| 7. |
Ten opzichte van
een rechthoekig assenstelsel Oxy is voor t
∈ R de kromme K gegeven door: |
| |
|
|
|
|
| |
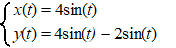 |
| |
|
|
|
|
| |
Bewijs dat de x-as een
raaklijn is van K. |
| |
|
|
|
|
| 8. |
examenvraagstuk Wiskunde
B VWO,
1988. Ten opzichte van
een rechthoekig assenstelsel Oxy is de kromme K gegeven door:
x = t2 - t
- 2 en y
= t2 + t + 1/4,
waarbij t ∈ R |
| |
|
|
|
|
| |
a. |
Bereken de
coördinaten van de gemeenschappelijke punten van K en de
coördinaatassen. |
| |
|
|
|
|
| |
b. |
Bereken de
coördinaten van de punten van K waarin de raaklijn aan K evenwijdig is
aan de x-as of aan de y-as. |
| |
|
|
|
|
| |
c. |
Onderzoek welke
waarden de richtingscoëfficiënten van de raaklijnen aan K kunnen
aannemen. |
| |
|
|
|
|
| 9. |
examenvraagstuk Wiskunde
B VWO,
1998. |
| |
|
|
|
|
| |
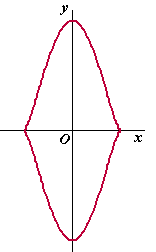
De kromme K is gegeven door: |
 |
| |
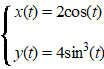 |
| |
|
|
| |
waarbij t
∈ [0, 2π]
In de figuur hiernaast is K getekend.
De coördinaatassen zijn symmetrie-assen van K. |
| |
|
|
| |
a. |
Toon aan dat voor t
≠ 0, p
en 2p de richtingscoëfficiënt van de
raaklijn aan K in het punt (x(t), y(t))
van K gelijk is aan -3sin2t |
| |
|
|
|
|
| |
R is een rechthoek waarvan
de zijden evenwijdig zijn aan de coördinaatassen. De hoekpunten van
R liggen op kromme K |
| |
|
|
|
|
| |
b. |
Bereken hoe groot de
oppervlakte van R maximaal kan zijn. |
| |
|
|
|
|
| |
Voor elke a ∈
R is de kromme Ka gegeven door: |
| |
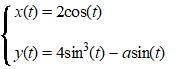 |
| |
|
|
|
|
| |
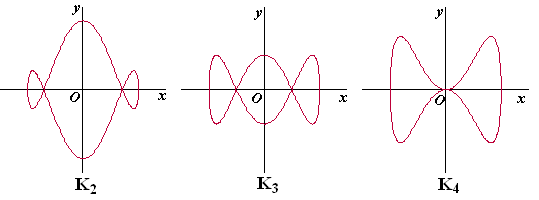
waarbij t
∈ [0, 2π]
Voor elke a zijn de coördinaatassen symmetrie-assen van Ka.
In de volgende figuur zijn K2, K3 en K4
getekend. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
K3 snijdt
zichzelf in het punt S op de positieve x-as. |
| |
|
|
|
|
| |
c. |
Bereken de hoek waaronder K3
zichzelf in S snijdt. |
| |
|
|
|
|
| |
|
|
|
 |