| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
| 1. |
Voor elk positief geheel getal n
bekijken we de baan Kn van een punt dat beweegt volgens: |
| |
|
|
|
| |
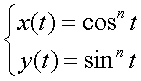 |
| |
|
|
|
| |
Met 0 ≤ t
≤ 0,5π
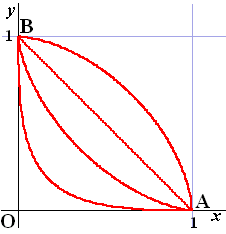
In de figuur hiernaast zijn vier banen getekend.
Gegeven een punt P van K6. |
 |
| |
|
|
| |
a. |
Toon aan dat de richtingscoŽfficiŽnt van
de raaklijn aan K6 in punt P gelijk is aan -tan4t |
| |
|
|
| |
In een punt P van K6 heeft de
raaklijn aan K6 richtingscoŽfficiŽnt -9. |
| |
|
|
| |
b. |
Bereken de coŲrdinaten van P. |
| |
|
|
| |
|
|
|
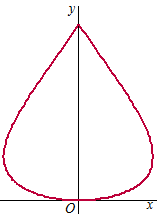
| 2. |
De "traan" hiernaast
voldoet aan de parametervergelijkingen: |
|
| |
|
|
|
| |
 |
 |
| |
|
|
| |
De traan past precies
in een gelijkbenige driehoek met als top het snijpunt van deze kromme
met de y-as: |
| |
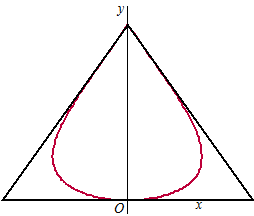 |
| |
|
|
|
| |
a. |
Bereken de exacte
oppervlakte van deze driehoek. |
| |
|
|
|
| |
b. |
De lijn y =
p snijdt de traan in de punten A en B zodat AB = 2.
Bereken algebraÔsch de exacte waarde van p waarvoor dat zo is. |
| |
|
|
|
| 3. |
Examenopgave VWO, Wiskunde B,
2015-II |
|
|
| |
De beweging van een punt P wordt beschreven door de
parametervoorstelling:
x(t) = cost
y(t) = sint ē cost
met 0 ≤ t ≤ 2πIn de volgende
figuur is de baan van P getekend. Deze baan wordt lemniscaat genoemd. |
| |
|
|
|
| |
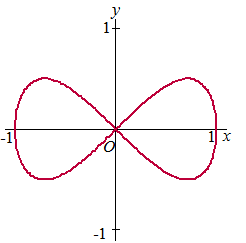 |
| |
|
|
|
| |
a. |
Tijdens de
beweging passeert punt P vier keer de lijn met vergelijking y
= 1/4
. Bereken
exact voor welke waarden van t dit het geval is. |
| |
|
|
|
| |
b. |
Tijdens de beweging gaat P twee keer door
de oorsprong O. De richtingen waarin P de
oorsprong passeert zijn verschillend. Bereken exact de hoek tussen deze
twee richtingen. |
| |
|
|
|
| 4. |
Examenopgave VWO, Wiskunde B,
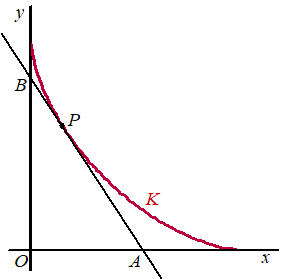
2021-II De kromme K
is gegeven door de bewegingsvergelijkingen:
x(t) = cos3t
y(t) = sin3t
met 0 < t < 1/2π
De raaklijn in een punt van deze kromme snijdt de x-as in punt A en de y-as in punt B.
Bewijs dat de
lengte van het lijnstuk AB constant is.
|
 |
| |
|
|
|
| 5. |
Examenopgave VWO, Wiskunde B,
2022-III
Gegeven zijn de bewegingsvergelijkingen: |
| |
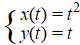 |
| |
|
|
|
| |
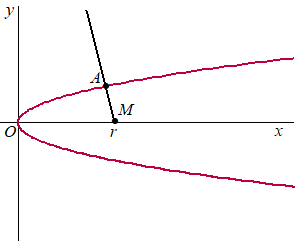
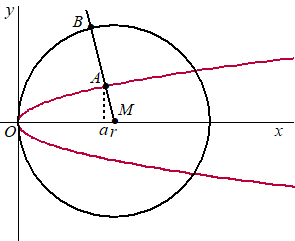
De bijbehorende baan is een parabool.
Punt M (r, 0) is een punt op de
positieve x-as met r >
1/2.
We kiezen punt A(a ,√a) op de
parabool zodanig dat de halve lijn vanuit M
door A de parabool loodrecht snijdt in punt
A.
Zie de figuur.
Er geldt: a = r
- 1/2 |
 |
| |
|
|
| |
a. |
Bewijs dit. |
| |
|
|
|
| |
We voegen de cirkel toe met middelpunt M(r,
0) en straal r.
Het punt O(0, 0) ligt op deze cirkel en op de
gegeven parabool.
De halve lijn vanuit M door A snijdt
de cirkel in punt B.
Zie de figuur hiernaast.
Voor een bepaalde waarde van r is A
het midden van lijnstuk MB. |
 |
| |
|
|
| |
b. |
Bereken
exact deze waarde van r. |
| |
|
|
|
| |
|
|
 |
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|