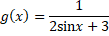| 3. |
De drie wieken van een
windmolen zitten vast in hun draaipunt op een hoogte van 25
meter boven de grond. Elke wiek is 10 meter lang, en de wieken
maken hoeken van 120º met elkaar.
Op tijdstip t = 0 staat één wiek recht omhoog.
De wieken maken op dit moment 80 omwentelingen per minuut, en
draaien op het plaatje tegen de klok in.
De hoogte van het uiteinde van deze wiek kun je het
makkelijkst beschrijven met een cosinusfunctie |

|
| |
|
|
|
a. |
Geef een vergelijking
voor de hoogte (in meter) van het uiteinde van deze wiek als
functie van de tijd t (in seconden). |
| |
|
|
|
b. |
Geef op algebraïsche wijze vier tijdstippen waarop het
uiteinde van deze wiek zich bevindt op 20 meter hoogte. |
| |
|
|
|
c. |
Geef vergelijkingen voor de uiteinden
van de andere twee wieken als functie van de tijd. |
|
|
|
|
|
|
| 4. |
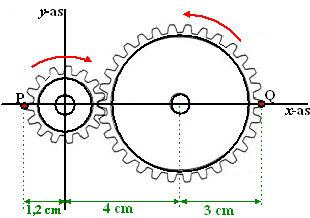
Twee tandwielen zijn
opgesteld als in de tekening hiernaast. Het kleinste wiel (15
tanden) heeft het middelpunt in de oorsprong en wordt
aangedreven zodat het ronddraait met 20 omwentelingen per
minuut.
Het grootste wiel (30 tanden) zit met het middelpunt vast in
punt (4,0) en gaat meedraaien.
Op tijdstip t = 0 is de situatie als hiernaast.
Punt P is een punt op de rand van het kleinste wiel, en punt Q
een punt op de rand van het grootste wiel.
|
|
| |
|
|
|
a. |
Geef een formule voor de x-coördinaat
van punt P als functie van de tijd t (in seconden). |
|
|
|
| |
|
|
Voor de x-coördinaat van punt
Q blijkt te gelden: xQ = 4 + 3cos(11/3πt). |
|
|
|
|
|
|
| |
|
|
|
b. |
Leg duidelijk uit waar deze formule
vandaan komt. |
| |
|
|
|
c. |
Bereken algebraïsch wanneer de x-coördinaat
van Q gelijk is aan 2,5 |
| |
|
|
0.5 + k • 1.5
1 + k • 1.5 |
|
|
d. |
Geef een formule voor de y-coördinaat
van punt Q en bereken daarmee algebraïsch wanneer die y-coördinaat
gelijk is aan 2. |
| |
|
|
|
|
0,17 + k • 1,5
0,58 + k • 1,5 |
|
|
|
|
|
|
|
| 5. |
Er schijnen bepaalde cycli te zijn die
bekend staan als ons "bioritme". Het zijn een soort
"inwendige klokken" in ons lichaam. Men onderscheidt
een Emotionele toestand, een Fysieke
toestand en een Intellectuele
toestand. Deze cycli beginnen op de dag van je geboorte vanuit hun
evenwichtsstand te stijgen, en volgen vanaf dat moment een sinusoïde.
Laten we de evenwichtsstand 50% nemen, en de maxima en minima 0%
en 100%.
De periode is voor de drie cycli verschillend: Emotioneel heeft
periode 28 dagen, Fysiek heeft periode 23 dagen en Intellectueel
heeft periode 33 dagen.
Er geldt: |
|
E(t) = 50 + 50sin(0,2244t)
F(t) = 50 + 50sin(0,2732t)
I(t) = 50 + 50sin(0,1904t) |
|
|
|
|
|
|
|
Daarin is t de tijd in dagen,
met t = 0 op je geboortedag. |
|
|
|
a. |
Bereken algebraïsch voor welke t je
Intellectuele cyclus gelijk is aan 10% |
| |
|
|
t = 18 +
k •33
t = 24 + k • 33 |
|
|
b. |
Bereken algebraïsch op hoeveel dagen gedurende je
eerste levensjaar je Emotionele cyclus hoger dan 80% is. |
| |
|
|
| |
|
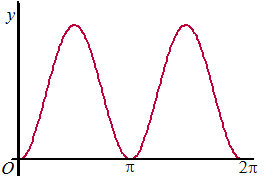
| 6. |
Gegeven is op interval
[0, 2π] de functie f(x)
= 1 - 5cos2x waarvan je de
grafiek hiernaast ziet.
De lijn y = a snijdt de grafiek van f in de
punten A en B zodat de oppervlakte van driehoek OAB
gelijk is aan 1/6
•
πa
Voor welke waarden van a is dat zo? |
 |
| |
|
|
| 7. |
Examenvraagstuk VWO Wiskunde B,
2016-II. |
| |
|
|
| |
In de Waddenzee varieert de waterhoogte in de loop
van de tijd. Eb en vloed wisselen elkaar voortdurend af in een
getijdencyclus met een periode van ongeveer 745 minuten. De
waterhoogte in het oostelijke deel van de Waddenzee kan worden
benaderd met de formule: h = 125 • cos(2πt/745) Hierbij is h de waterhoogte in cm ten
opzichte van NAP (Normaal Amsterdams Peil) en is t de tijd in
minuten. Tijdstip t
=
0 komt overeen met een moment waarop
h = 125
.
In het oostelijk deel van de Waddenzee liggen
verschillende zandbanken die gedurende een deel van een
getijdencyclus droog komen te liggen.
De droogligtijd D is het aantal minuten per
getijdencyclus dat een zandbank niet geheel onder water ligt. De
droogligtijd hangt af van de hoogte van de zandbank: de hoogte van
het hoogste punt van de zandbank ten opzichte van NAP.
In het oostelijk deel van de Waddenzee bevindt zich
een zandbank met een hoogte van 40 cm boven NAP.
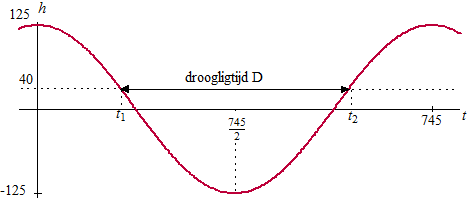
In onderstaande figuur is de grafiek van de waterhoogte h
getekend. Tevens is de hoogte van deze zandbank weergegeven.
Gedurende één periode zijn er twee tijdstippen waarop de waterhoogte
h gelijk is aan de hoogte van de zandbank. We noemen deze
tijdstippen t1 en t2 . Het
verschil tussen t2 en t1 is de
droogligtijd D. |
| |
|
|
| |
 |
| |
|
|
| |
a. |
Bereken algebraïsch de droogligtijd D van deze zandbank.
Rond je antwoord af op een geheel aantal minuten. |
| |
|
|
| |
Op drooggevallen zandbanken kunnen waddenvogels
voedsel vinden. Daarom willen natuuronderzoekers het verband weten
tussen de hoogte van de zandbanken en de tijd dat ze droog liggen.
Met z duiden we de hoogte in cm van de
zandbank aan, ten opzichte van NAP. Er geldt dan:
z = 125 • cos(π - π • D/745) |
| |
|
|
| |
b. |
Bewijs dit. |
| |
|
|
| 8. |
Examenvraagstuk HAVO Wiskunde B,
2017-I |
| |
|
|
| |
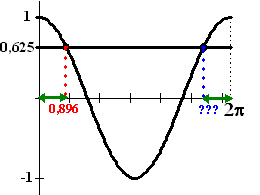
De functie g
is gegeven door: |
| |
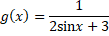 |
| |
|
| |
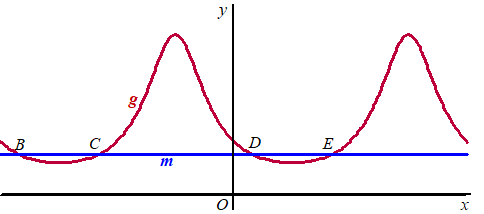
De lijn m is gegeven door y
= 1/4.
Op het interval [-2π, 2π]
snijdt m de grafiek van
g achtereenvolgens in de punten B, C, D
en E. Zie de volgende figuur. |
| |
|
| |
 |
| |
|
| |
Bereken exact
de afstand tussen B en E |
| |
|
| |
|
| |
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|