|
|||||
| 1. | a. | 2sin(x + 1/6π)
= 1 sin(x + 1/6π) = 0,5 x + 1/6π = 1/6π + k2π ∨ x + 1/6π = π - 1/6π + k2π x = 0 + k2π ∨ x = 4/6π + k2π In [0, 2p] zijn de oplossingen {0, 2/3π, 2π} |
|||
| b. | 3 - 4sin(2x) = 2 -4sin(2x) = -1 sin(2x) = 0,25 2x = 0,25 + k2π ∨ 2x = π - 0,25 + k2π x = 0,13 + kπ ∨ x = 1,44 + kπ In [0, 2π] zijn de oplossingen {0.13, 1.44, 3.27, 4.58} |
||||
| c. | 3 - sinx = 5 - 2sinx -sinx + 2sinx = 5 - 3 sinx = 2 Geen oplossing |
||||
| d. | 2 - sin(3x) = 1,8 sin(3x) = 0,2 3x = 0,20 + k2π ∨ 3x = π - 0,20 + k2π x = 0,07 + k2/3π ∨ x = 0,98 + k2/3π In [0, 2π] zijn de oplossingen {0.07, 0.98, 2.16, 3.07, 4.26, 5.17} |
||||
| e. | 1 + sin(x + 1/2π)
= 1,5 sin(x + 1/2π) = 0,5 x + 1/2π = 1/6π + k2π ∨ x + 1/2π = π - 1/6π + k2π x = -2/6π + k2π ∨ x = 2/6π + k2π In [0, 2π] zijn de oplossingen {1/3π, 12/3π} |
||||
| f. | 6 - 2 sin(2x -
π) = 5 2 sin(2x - π) = 1 sin(2x - π) = 0,5 2x - π = 1/6π + k2π ∨ 2x - π = π - 1/6π + k2π 2x = 11/6π + k2π ∨ 2x = 15/6π + k2π x = 7/12π + kπ ∨ x = 11/12π + kπ In [0, 2π] zijn de oplossingen {7/12π, 11/12π, 17/12π, 111/12π} |
||||
| 2. | a. | 50 periodes per
seconde betekent dat één periode 1/50 = 0,02
seconde duurt. Dan staat in de formule 2π/0,02 = 314. |
|||
| b. | 100 =
220sin(314t) 0,4545 = sin(314t) 314t = 0,472 + k2π ∨ 314t = π - 0,472 + k2π t = 0,0015 + k 0,02 ∨ t = 0,0085 + k 0,02 Daartussen ligt 0,0085 - 0,0015 = 0,0070 seconden van een volledige periode van 0,02 seconde. Dat is 0,0070/0,02 100% = 35% |
||||
| 3. | a. | Evenwichtslijn
h = 25 Amplitude 10 Periode: 1/80 minuut = 0,0125 dus in de formule staat 2π/0,0125 = 502,65 Beginpunt is in een maximum, dus de formule is h(t) = 25 + 10 cos(502,65t) |
|||
| b. | 20 = 25 + 10
cos(502,65t) -5 = 10 cos(502,65t) -0,5 = cos(502,65t) 502,65t = 2,09 + k2π ∨ 502,65t = 2π - 2,09 + k2π t = 0,0042 + k 0,0125 ∨ t = 0,0083 + k 0,0125 |
||||
| c. | amplitude, periode en
evenwichtslijn zijn hetzelfde als voor de eerste wiek. De wiek rechtsonder is pas in de top na 1/3 periode, en dat is 0,0125 1/3 = 0,00417 seconden. De formule is daarom h(t) = 25 + 10 cos(502,65(t - 0,00417)) De wiek linksonder is pas in de top na 2/3 periode, en dat is 0,0125 2/3 = 0,00833seconden. De formule is daarom h(t) = 25 + 10 cos(502,65(t - 0,00833)) |
||||
| 4. | a. | Evenwichtslijn is
x = 0 Amplitude is 1,2 Periode is 1/20 minuut is 3 seconden. Dus in de formule staat 2π/3 Beginpunt is in het minimum, dus we maken er een gespiegelde cosinus van. x(t) = -1,2 cos(2πt/3) |
|||
| b. | xQ
= 4 + 3cos(1/3πt). Evenwichtslijn x = 4 Amplitude 3 periode: in 3 seconden komen 15 tanden voorbij (wiel 1) dus 30 tanden duurt 6 seconden. In de formule staat daarom 2π/6 = 1/3π Beginpunt is in het maximum, dus een cosinusfunctie |
||||
| c. | 4 + 3cos(1/3πt)
= 2,5 3cos(1/3πt) = -1,5 cos(1/3πt) = -0,5 1/3πt = 1/3π + k2π ∨ 1/3πt = 2π - 1/3π + k2π t = 1 + k 6 ∨ t = 5 + k 6 |
||||
| d. | Evenwichtslijn is
y = 0 Amplitude is 3 Periode is 6 seconden, dus in de formule staat daarom 2π/6 = 1/3π Beginpunt in 0 en gaat omhoog, dus we nemen een gewone sinus y = 3sin(1/3πt) 2 = 3sin(1/3πt) sin(1/3πt) = 2/3 1/3πt = 0,73 + k2π ∨ 1/3πt = π - 0,73 + k2π t = 0,70 + k 6 ∨ t = 2,30 + k 6 |
||||
| 5. | a. | 50 + 50sin(0,1904t)
= 10 50sin(0,1904t) = -40 sin(0,1904t) = -0,8 0,1904t = -0,93 + k2π ∨ 0,1904t = π - - 0,93 + k2π t = -4,87 + k 33 ∨ t = 21,37 + k 33 |
|||
| b. | 50 + 50sin(0,2244t)
= 80 50sin(0,2244t) = 30 sin(0,2244t) = 0,6 0,2244t = 0,644 + k2π ∨ 0,2244t = π - 0,644 + k2π t = 2,87 + k 28 ∨ t = 11,13 + k 28 Hoger dan 80% is tijdens de eerste periode op de dagen t = 3, 4, 5, 6, ..., 11 en dat zijn er 9 Een periode duurt 28 dagen dus in een jaar zijn er 365/28 =13 periodes. Dan zal E 13 9 = 117 dagen hoger dan 80% zijn. |
||||
| 6. | De oppervlakte van de
driehoek is 1/2
basis hoogte = 1/2
basis a Als dat gelijk is aan 1/6πa dan moet gelden basis = 1/3π Er zijn drie mogelijkheden: |
||||
|
|
|||||
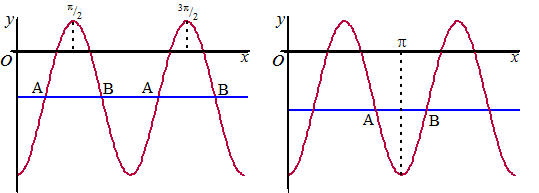
| Mogelijkheden 1 en 2 staan in de linkerfiguur. Omdat de grafiek symmetrisch is in de lijnen x = 1/2π en x = 3/2π geeft dat de mogelijkheden: | |||||
| 1. | xA
= 1/2π
- 1/6π
= 1/3π
en xB = 1/2π
+ 1/6π
= 2/3π in dat geval is a = 1 - 5cos2 (1/6π) = 1 - 5 1/4 = -1/4 |
||||
| 2. | xA
= 3/2π
- 1/6π
= 4/3π
en xB = 3/2π
+ 1/6π
= 5/3π in dat geval is a = 1 - 5cos2 (4/3π) = -1/4 |
||||
| Mogelijkheid 3 staat in de rechterfiguur. Omdat de grafiek symmetrisch is in x = π geeft dat: | |||||
| 3. | xA
=
π - 1/6π
= 5/6π
en xB =
π +
1/6π
= 7/6π in dat geval is a = 1 - 5cos2(5/6π) = 1 - 5 3/4 = -21/4 |
||||
| 7. | a. | 125cos(2π/745
t) = 40 cos(2π/745 t) = 0,32 2π/745 t = 1,245 + k2π ∨ 2π/745 t = -1,245 + k2π t = 147,62 + k 745 ∨ t = 597,38 + k 745 Daartussen ligt D = 450 minuten |
|||
| b. | z = h(t1) = 125
cos(2π/745 t1) Als de droogligtijd D is, dan blijft er van de periode van 745 minuten nog (745 - D) minuten over waarin het water hoger staat dan de zandbank. Uit de symmetrie van de grafiek volgt dat dat er aan beide zijden een stuk van 0,5(745 - D) zit, en dat is gelijk aan t1. t1 = 0,5(745 - D) invullen in de z-formule: z = 125 cos(2π/745 (0,5 (745 - D)) z = 125 cos(π/745 (745 - D)) z = 125 cos(π - π/745 D) |
||||
| 8. | 1/(2sinx + 3) =
1/4 2sinx + 3 = 4 2sinx = 1 sinx = 1/2 x = 1/6π + k2π ∨ x = 5/6π + k2π xB = 1/6π - 2π = -15/6π xE = 5/6π De afstand is dan 15/6π + 5/6π = 22/3π |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||