|
|
 |
|
Gelijkvormigheid. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Elke keer als je dingen (foto's
of kopieën of Russische poppen zoals hiernaast) gaat vergroten of
verkleinen, dan wil je graag dat de vorm van je figuren gelijk blijft.
Het enige dat moet veranderen is dat alle lengtes gewoon een aantal keer
zo groot of zo klein worden.
Wat betekent het nou als je zegt dat de "vorm" gelijk moet blijven? Nou,
dat betekent eigenlijk dat alle hoeken van de nieuwe
figuur gelijk zijn aan de overeenkomstige hoeken van de originele
figuur. |
 |
| |
|
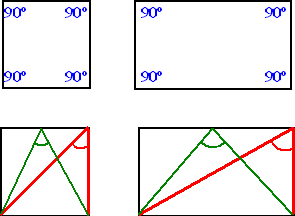
Dus niet alleen de hoeken van de omtrek, nee
alle. Kijk maar naar het vierkant en de rechthoek hiernaast.
Die hebben zoals je in de bovenste tekening ziet alle vier de hoeken
gelijk (90º) maar hebben beslist niet dezelfde vorm.
In de onderste figuur zijn de rode hoeken bijvoorbeeld beslist niet
gelijk en ook de groene hoeken niet.
Je zag natuurlijk ook meteen al wel dat deze twee figuren niet dezelfde
vorm hebben: de eerste is een vierkant en de tweede niet! |
 |
| |
|
| Twee figuren zijn
gelijkvormig: |
| |
|
|
• |
alle
overeenkomstige hoeken zijn gelijk |
|
• |
alle
overeenkomstige lengtes hebben een zelfde verhouding |
|
|
| |
|
|
Gelijkvormige driehoeken. |
| |
|
Driehoeken vormen hier een
speciale uitzondering.
Voor gelijkvormige driehoeken geldt natuurlijk ook dat alle
overeenkomstige hoeken gelijk zijn, maar het is daarvoor genoeg als "de"
drie hoeken van de driehoek gelijk zijn. Andere hoeken binnen zo'n
driehoek zijn dan
automatisch ook gelijk.
Waarom dat nou precies zo is zou hier iets te ver voeren. Als je het
écht graag wilt weten, en je kunt vannacht anders minder goed slapen,
dan moet je de verdieping hiernaast maar lezen. |
| |
 |
| Twee
driehoeken zijn
gelijkvormig: |
| |
|
| • |
De drie hoeken
zijn gelijk. |
| • |
De zijden hebben
een zelfde verhouding. |
|
|
| |
|
Het kan natuurlijk zelfs nóg
sterker: het is al genoeg als twéé hoeken gelijk zijn. Omdat ze samen
immers altijd 180º zijn is de derde hoek dan ook automatisch bekend.
Denk er goed aan dat de twee voorwaarden hierboven elk apart genoeg zijn
om aan te tonen dat twee driehoeken gelijkvormig zijn. Zodra de ene
voorwaarde geldt, geldt de andere ook automatisch.
Wat kunnen we hiermee?
|
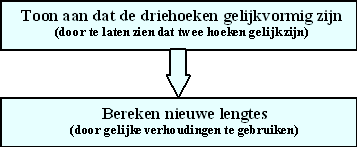
Deze eigenschap van driehoeken kunnen we makkelijk gebruiken om lengtes
van lijnstukken uit te gaan rekenen
Het werkschema zal er daarbij meestal zó uitzien: |
| |
|
|
 |
| |
|
Voor die twee hoeken zul je
meestal gebruik maken van Z-hoeken of F-hoeken of overstaande
hoeken.
Voor het berekenen van verhoudingen kun je het handigst een
verhoudingsschema maken. Denk er goed om dat overeenkomstige zijden
daarin ook onder elkaar staan! |
| |
|
|
Notatie. |
| |
|
| Als twee driehoeken ABC en DEF
gelijkvormig aan elkaar zijn, dan noteren we dat als: |
| |
|
|
|
| |
|
| Wen jezelf aan om de
overeenkomstige hoekpunten ook op dezelfde plaats te zetten, dat is
handig voor het maken van een verhoudingsschema. De notatie hierboven
zou betekenen dat hoek A gelijk is aan hoek D, en hoek B aan hoek E, en
hoek C aan hoek F. |
| |
|
Voorbeeld.
In een rechthoekige driehoek ABC met rechte hoek A en zijden AB = 8 en
AC = 10, is vanaf het midden M van zijde BC een lijn loodrecht op
BC getrokken, die AB snijdt in P.
Bereken de lengte MP.
Eerst maar even BC met Pythagoras uitrekenen:
BC2 = 82 + 62 = 100 dus BC
= 10.
Nu gaan we op jacht naar gelijke hoeken. |
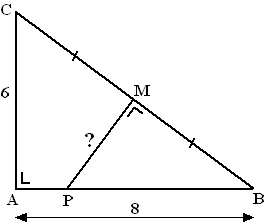 |
| Maak hoek B rood en hoek C blauw. |
|
Dan zijn rood en blauw samen 90º, immers samen met hoek A zijn
de 180º.
Maar de rode hoek plus hoek BPM zijn samen óók 90º, dat kun je
zien in driehoek MBP
Dat kan alleen maar betekenen dat hoek BPM óók blauw moet zijn!
Je ziet nu dat de driehoeken MBP en ABC dezelfde hoeken hebben
dus zijn ze gelijkvormig (je had trouwens al meteen mogen
zeggen dat deze driehoeken twéé hoeken gelijk hebben, namelijk
een rechte en een rode, dus dat ze gelijkvormig moeten zijn, had
je dat al gezien?)
Conclusie: MBP ~ ABC (denk
om de volgorde).
Dan kunnen we voor de zijden van deze driehoeken een
verhoudingsschema maken: (bedenk dat MB de helft van BC is)
| |
AB
8 |
BC
10 |
AC
6 |
MB
5 |
BP
? |
MP
? |
|
| |
|
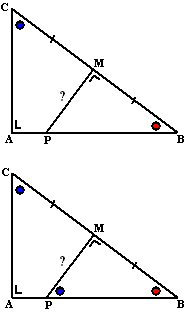 |
| Uit dit schema volgt vrij eenvoudig dat
BP
= 10 • 5/8 = 6,25 (zonder
schema kan het ook direct met verhoudingen: AB : AC = MB :
MP dus 8/6 = 5/MP
dus MP = 3,75) |
|
| |
|
|
Drie Basisfiguren. |
|
| |
|
| Er zijn drie basisfiguren voor
gelijkvormige driehoeken die zó vaak voorkomen dat het de moeite waard
is ze uit je hoofd te leren zodat je ze snel in figuren kunt herkennen. |
| |
|
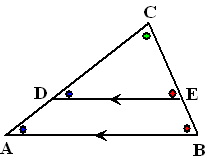
Figuur 1:
In de figuur hiernaast is DE evenwijdig aan AB.
Omdat dat zo is, zijn de blauwe hoeken bij A en D gelijk, en ook
de rode hoeken bij B en E. Dat zijn namelijk F-hoeken.
Dus hebben de driehoeken CDE en CAB dezelfde hoeken.
|
 |
| |
|
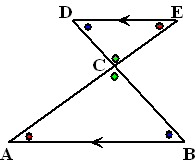
Figuur 2: De Zandloper.
In de figuur hiernaast is DE evenwijdig aan AB.
Omdat dat zo is zijn de blauwe hoeken D en B gelijk en de rode
hoeken E en A ook. Dat zijn namelijk Z-hoeken.
Ook de groene hoeken bij C zijn gelijk: overstaande hoeken.
Dus hebben de driehoeken CDE en CBA dezelfde hoeken.
|
 |
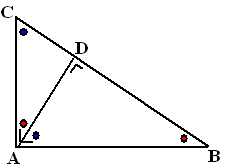
Figuur 3:
ABC is een rechthoekige driehoek met rechte hoek A. De
hoogtelijn AD vanuit de rechte hoek op de bissectrice is
getekend.
Om precies dezelfde redenen als in het voorbeeld hierboven zijn
de hoeken met dezelfde kleur gelijk. Rood plus blauw is samen
90º.
Nu zijn er zelfs drie gelijkvormige driehoeken te zien:
|
 |
|
| |
|
|
Een onbekende in het
verhoudingsschema. |
| |
|
Neem de driehoek hiernaast, waarvan we graag
CE en DE willen berekenen. Je herkent hier intussen waarschijnlijk
wel figuur 1 van hierboven.
Dat betekent dat driehoeken ABC en DEC gelijkvormig zijn.
Een verhoudingsschema zie er zó uit:
|
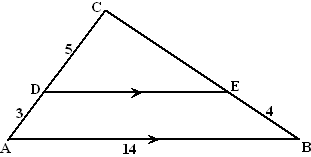 |
Kijk, DE dat wil nog wel:
DE = 14 • 5/8 = 8,75
Maar daarna loopt het vast! De andere lijnstukken BC en EC uit deze
tabel zijn beiden onbekend.
De oplossing komt door gewoon te stellen dat CE gelijk is aan x.
Dan is BC namelijk gelijk aan x + 4 en dan ziet de
verhoudingstabel er zó uit:
| |
AB
14 |
BC
x + 4 |
AC
8 |
DE
8,75 |
EC
x |
DC
5 |
|
| |
En dan kun je kruislings vermenigvuldigen: 5 • (x + 4) =
8 • x
Dan is het verder eenvoudig: 5x + 20 = 8x
dus 3x = 20 en x = 62/3
Conclusie: EC = 62/3
en BC = 102/3.
|
| |
|
| |
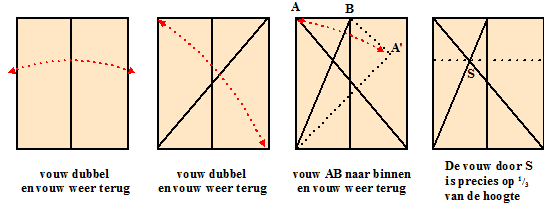
Leuk
Origami-toepassinkje...
Origami is de kunst van het papiervouwen. Je kunt er mooie dingen als de
zwaan hiernaast mee vouwen. Als een Origami-vouwer (origamist?)
een velletje papier in drieën moet vouwen, dan doet hij dat natuurlijk
niet door gewoon de lengte te meten en dat dan door drie te delen, nee
hij doet dat uitsluitend door te vouwen!
Dat gaat zoals in het stripverhaal hieronder: |
 |
| |
|
|
 |
| |
|
Jij ziet natuurlijk in één
oogopslag hoe hier handig gebruik is gemaakt van gelijkvormigheid!
Toch? |
| |
|
|
OPGAVEN |
| |
|
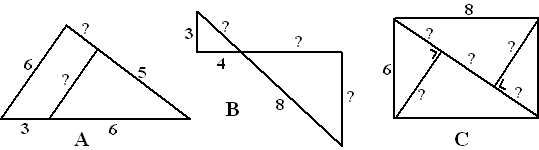
| 1. |
Bereken de vraagtekens in de onderstaande
figuren. |
| |
|
|
|
| |
|
|
|
| |
 |
| |
|
|
A: 4 en 2,5
B: 5 en 6,4 en 4,8
C: 3,6 en 2,8 en 4,8 |
|
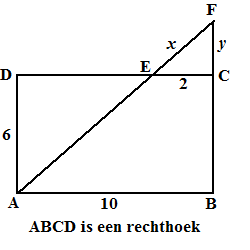
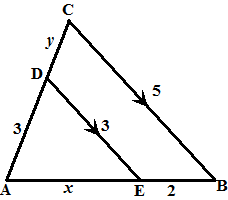
| 2. |
Bereken x en y in de
volgende figuren: |
| |
|
|
|
| |
 |
 |
| |
|
|
|
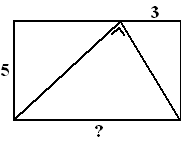
| 3. |
Hiernaast is in een rechthoek een
rechthoekige driehoek getekend.
Bereken de lengte van de zijde met het vraagteken. |
 |
| |
|
|
|
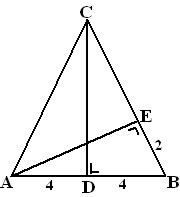
| 4. |
In een gelijkbenige driehoek met basis 8 worden
twee hoogtelijnen getekend. Zie de figuur hiernaast.
Het blijkt dat EB = 2
|
 |
| |
|
|
| |
a. |
Toon aan dat de hoeken BAE en DCB gelijk zijn. |
| |
|
|
| |
b. |
Bereken de oppervlakte van driehoek ABC |
| |
|
|
| |
|
|
|
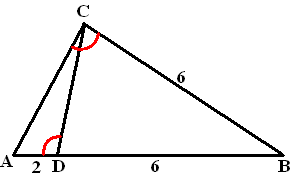
| 5. |
Punt D is zo gekozen
dat AD = 2 en BD = 6
Het blijkt dat de hoeken ADC en ACB gelijk zijn.
Bereken de lengte van CD. |
 |
| |
|
|
| |
|
|
|
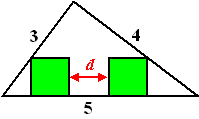
| 6. |
Uit een wiskunde-Olympiade
Over de schuine zijde van een rechthoekige driehoek met zijden
3, 4 en 5 schuift men twee vierkantjes met zijden 1 zo ver
mogelijk naar buiten (tot ze de rechthoekszijden raken). Bereken
de afstand d tussen beide vierkantjes. |
 |
| |
|
|
|
| |
|
|
|
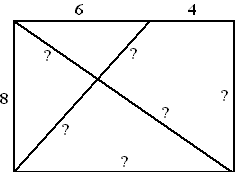
| 7. |
Hiernaast staat een
rechthoek met daarin twee lijnstukken getekend.
Bereken de vraagtekens in deze figuur.
Geef je antwoorden in twee decimalen nauwkeurig. |
 |
| |
|
|
|
4,80 en 8,01
en 3,75 en 6,25 |
|
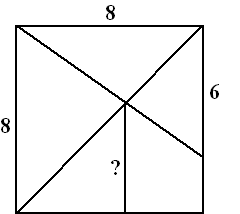
| 8. |
Bereken de lengte van
het lijnstuk met het vraagteken in het vierkant hiernaast op
twee decimalen nauwkeurig. |
 |
| |
|
|
| |
|
|
|
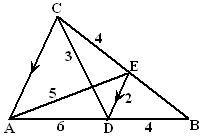
| 9. |
Bereken in de figuur hiernaast
de lengtes van alle niet-aangegeven lijnstukken, als gegeven is dat DE evenwijdig is aan
AC. |
 |
| |
|
|
|
| |
|
|
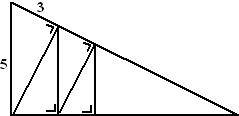
| 10. |
Bereken de lengtes van
alle lijnstukken in de rechthoekige driehoek hiernaast.
Controleer na afloop of in de gehele driehoek de stelling van
Pythagoras wel klopt. |
 |
| |
|
|
|
| |
|
|
|
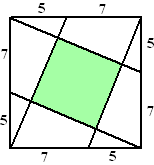
| 11. |
Hiernaast staat een
vierkant van 12 bij 12 waarin een kleiner vierkant is getekend.
Bereken de oppervlakte van dat kleinere vierkant. |
 |
| |
|
|
|
| |
|
 |
| 12. |
Een bewijs van de
stelling van Pythagoras.
Er bestaan een heleboel verschillende bewijzen voor de stelling
van Pythagoras. In deze opgave zullen we deze stelling gaan
bewijzen met behulp van gelijkvormige driehoeken. |
| |
|
|
| |
Teken een rechthoekige driehoek ABC
met rechte hoek C. Teken ook de hoogtelijn CD vanuit C op AB.
Noem de zijden AB = c, AC = b en BC = a
|
| |
|
|
| |
a. |
Druk AD uit in b en
c.
Druk BD uit in a en c. |
| |
|
|
| |
b. |
Toon aan dat a2
+ b2 = c2 |
| |
|
|
|
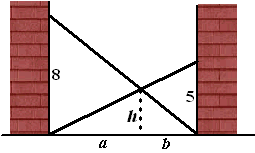
 13. 13. |
Twee ladders staan in een smal
steegje schuin van de voet van de ene muur naar de andere muur.
Het zijaanzicht is hiernaast getekend. De toppen van de ladders
raken de muren op hoogtes 8 en 5 meter.
Het gaat erom de hoogte h van het punt waar zij elkaar
raken boven de grond te bepalen.
Neem de lengtes a en b als in de figuur hiernaast. |
 |
| |
|
|
| |
a. |
Toon aan dat geldt 8b = h • (a +
b)
en ook dat geldt 5a = h • (a + b) |
| |
|
|
|
| |
b. |
Bereken uit deze twee vergelijkingen de hoogte
h |
|
| |
|
|
|
| |
|
|
|
 |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|