| 1. |
Construeer de conflictlijnen van de volgende
groene gebieden. vermeld bij je tekening uit welke vormen de
delen van de conflictlijnen bestaan. |
| |
|
| |
|
| |
|
| |
|
|
|
| 2. |
examenvraagstuk |
| |
|
|
|
| |
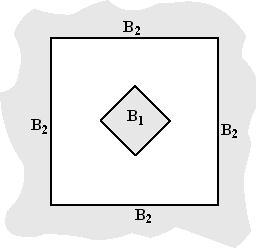
In de figuur hieronder is binnen een groot
vierkant een kleiner vierkant getekend. De vierkanten hebben het zelfde
middelpunt en zijn 45 º ten opzichte van elkaar gedraaid. B1
is het binnengebied van het kleine vierkant, B2 is het
buitengebied van het grote vierkant. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
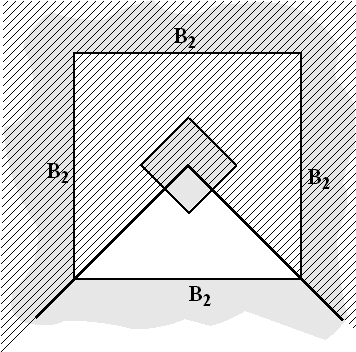
In de figuur hieronder is driekwart van
deze figuur afgedekt. Teken in het resterende kwart de
conflictlijn van B1 en B2.
Licht je tekening toe. |
| |
|
|
|
| |
 |
| |
|
|
|
| 3. |
examenvraagstuk. |
| |
|
| |
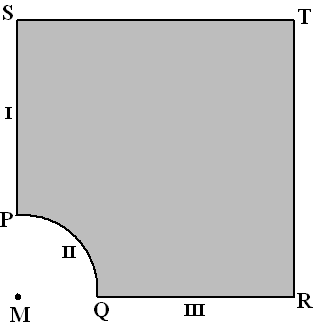
Het grijze gebied in de figuur hieronder is
een deel van het vierkant MRTS met zijde 7. De grens PQ is een kwartcirkel
met middelpunt M en straal 2. Er zijn drie landen, I, II en III, die alle
drie aan het grijs gekleurde gebied grenzen. De grenzen met die landen
zijn respectievelijk SP, PQ en QR.
Het grijze gebied wordt onder de drie landen verdeeld volgens het
naaste-buur-principe. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In het grijze gebied ligt op de lijn MT een
punt P dat even ver van de drie landen ligt. |
| |
|
|
|
| |
a. |
Bereken de afstand van D tot de drie landen in twee
decimalen nauwkeurig. |
| |
|
|
|
| |
b. |
Teken in de figuur de conflictlijnen tussen de drie
landen in het grijze gebied. Licht je werkwijze toe. |
| |
|
|
|
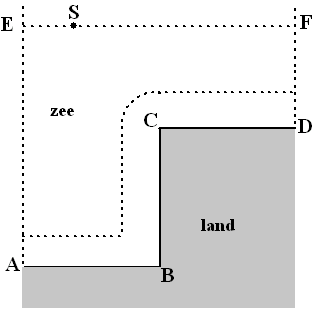
| 4. |
Examenvraagstuk VWO Wiskunde B,
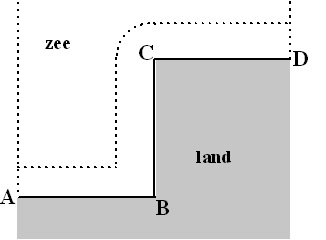
2002. Een kustlijn bestaat uit drie
rechte stukken AB, BC en CD, die hoeken 90º met elkaar maken. De lengte
van elk recht stuk is 4 kilometer. Zie de figuur hieronder.
In de figuur zijn twee stippellijnen getekend die loodrecht staan op AB
en CD. In deze opgave beperken we ons tot het gebied tussen deze
stippellijnen.
De lengte van de iso-afstandslijn (in kilometers) tussen de
stippellijnen, op een afstand van x kilometer uit de kust, noemen
we L(x). |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In deze figuur is een
iso-afstandslijn getekend, x kilometer uit de kust. De lengte van
deze iso-afstandslijn wordt gegeven door: L(x) = 12 - 2x
+ 1/2πx |
| |
|
|
|
| |
a. |
Toon dat aan. |
|
| |
|
|
|
| |
b. |
Deze formule geldt alleen voor
x £ 4; voor x > 4 geldt een
andere formule voor L(x). Zonder deze andere formule te kennen
kun je beredeneren tot welke waarde L(x) nadert als x
nadert tot oneindig.
Bereken die waarde. |
| |
|
|
|
| |
In de figuur hieronder liggen
de punten E en F op de stippellijnen die loodrecht op AB en CD staan. EF
is evenwijdig aan AB en CD. De afstand van EF tot CD is 3 kilometer. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Een speedboot S vaart met een
snelheid van 1 km per minuut van E naar F. We noemen de afstand (in km)
van S tot de kust na t minuten varen K(t).
Voor 4 ≤ t ≤
8 geldt: K(t) = 3. |
| |
|
|
|
| |
c. |
Toon aan dat voor 0
≤
t ≤ 4 geldt: K(t)
= √(t2 - 8t + 25) |
| |
|
|
|
| 5. |
Examenvraagstuk VWO Wiskunde B, 2003.
Gegeven zijn een lijn k
en twee punten A en B op gelijke afstand van k en aan dezelfde
kant van k. Zie de figuur hieronder. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
We verdelen het vlak waar A, B
en k in liggen volgens het naaste-buur principe. De grenslijnen
van deze verdeling zijn conflictlijnen.
Het punt D is het 'drielandenpunt' , dat is het punt op gelijke afstand
van A, B en k |
| |
|
|
|
| |
a. |
Teken in de figuur het
drielandenpunt D. Licht je werkwijze toe. |
| |
|
|
|
| |
b. |
Teken in de figuur de
conflictlijnen. Licht je werkwijze toe. |
| |
|
|
|
| 6. |
Examenvraagstuk VWO Wiskunde B, 2003. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
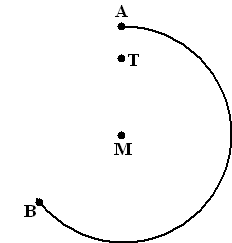
Santorini is een Grieks eiland. Door een
vulkaanuitbarsting ruim 3550 jaar geleden is meer dan de helft van het
eiland verzonken in zee. Het overgebleven deel van het eiland heeft de
vorm van een croissant. Zie de figuur hierboven.
Geïnspireerd door de merkwaardige vorm van dit eiland gaan we over
op het volgende wiskundige model.
Boog AB is een gedeelte van een cirkel met middelpunt M en straal MA. De
punten A, T en M liggen op één lijn. Zie de figuur hiernaast.
Veronderstel dat het vlak volgens het
naaste-buur-principe wordt verdeeld tussen T en boog AB. De grens bestaat
uit twee rechte delen en één gebogen deel. |
 |
| |
|
|
|
| |
Teken de grens in de figuur en geef bij elk van de drie
delen een toelichting. |
| |
|
|
|
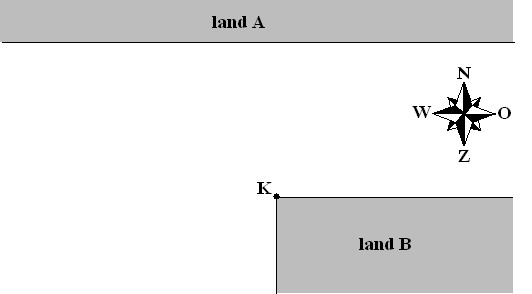
| 7. |
Examenvraagstuk VWO Wiskunde B, 2005. Twee landen A en B worden gescheiden door een
zee. De kustlijn van A is recht en loopt west-oost. De kustlijn van B
maakt bij kaap K een hoek van 90º; een deel van de kustlijn loopt
noord-zuid en een deel west-oost. De afstand tussen de kustlijnen die
west-oost lopen is 40 km. Zie onderstaande figuur. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Beide landen maken aanspraak op een deel van
de zee. Ze vinden beide dat de strook tot 30 km uit de kust hen
toebehoort. Voor een groot deel van de zee zijn de landen het erover eens
van wie het is, maar een deel van de zee blijft betwist gebied. |
| |
|
|
|
| |
a. |
Arceer in de figuur het betwiste gebied. |
|
| |
|
|
|
| |
De zee zou verdeeld kunnen worden volgens het
naaste-buur-principe. |
| |
|
|
|
| |
b |
Teken in de figuur de hierbij behorende
grenslijn. Licht je werkwijze toe. |
| |
|
|
 |
| |
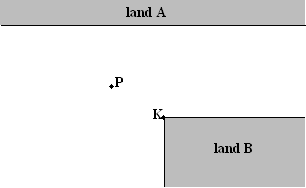
In de figuur hiernaast is een
punt P getekend van de grenslijn bij verdeling volgens het
naaste-buur-principe. Het betwiste gebied heeft een noordrand en een
zuidrand. |
| |
|
|
| |
c. |
Toon aan dat P even ver van beide randen
afligt. |
| |
|
|
|
| 8. |
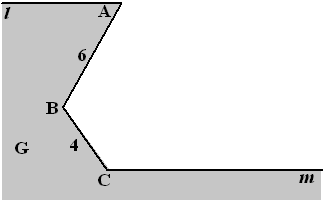
Examenvraagstuk VWO Wiskunde B, 2006. Een gebied G wordt begrensd door de
lijnstukken AB en BC, de halve lijn l met beginpunt A en de halve
lijn m met beginpunt C. Zie onderstaande figuur. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Verder is gegeven AB = 6, BC = 4, de
hoek tussen l en AB is 60º, ÐABC en de
hoek tussen BC en m zijn 120º
Uit deze gegevens volgt dat l evenwijdig is aan m. |
| |
|
|
|
| |
a. |
Bewijs dat. |
 |
| |
|
|
| |
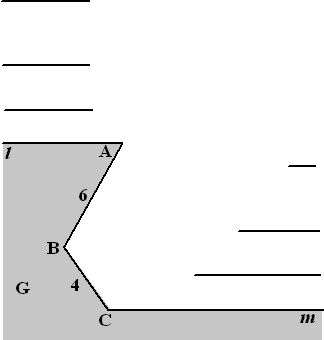
De iso-a-lijn van G wordt gevormd door de
punten die op afstand a van gebied G liggen. Elke iso-a-lijn
van G bevat twee halve lijnen en een cirkelboog.
Voor kleine waarden van a bevat de iso-a-lijn daarnaast ook
nog één of twee lijnstukken.
Voor een aantal waarden van a is in de figuur hiernaast een begin
gemaakt met het tekenen van de iso-a-lijn. |
| |
|
|
| |
b. |
Teken in deze figuur de ontbrekende delen
van deze drie iso-a-lijnen. |
| |
|
|
| |
Voor waarden van a die
groter zijn dan een zekere waarde bestaat de iso-a-lijn uitsluitend
uit twee halve lijnen en een cirkelboog QP.
De eindpunten Q van deze cirkelbogen liggen op een halve lijn die
loodrecht op l staat. |
| |
|
|
|
| |
c. |
Teken de verzameling van de eindpunten P.
Beschrijf deze verzameling. |
| |
|
|
|
| 9. |
Examenvraagstuk VWO Wiskunde B, 2007. |
| |
|
|
 |
| |
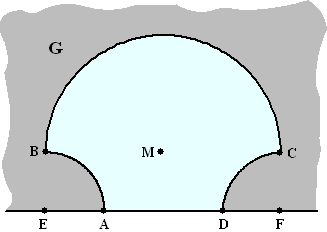
Een gebied G heeft aan een van
zijn rechte zijden, EF, een inham, waarvan de rand bestaat uit drie
cirkelbogen: |
| |
- |
boog AB is een kwartcirkel met
straal 3 en middelpunt E |
| |
- |
boog CD is een kwartcirkel met
straal 3 en middelpunt F |
| |
- |
boog BC is een halve cirkel met
straal 6 en middelpunt M |
| |
- |
E, A, D en F liggen op een
rechte lijn. |
| |
|
|
|
| |
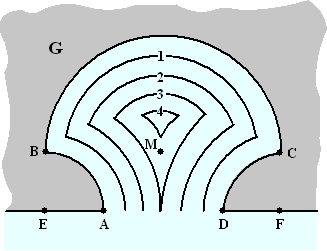
In de
figuur hiernaast zijn in
de inham de iso-afstandslijnen getekend op de afstanden 1, 2, 3 en 4 van
het land. |
 |
| |
|
|
| |
a. |
Teken in de bovenste figuur de
iso-afstandslijn waarop punt M ligt. Licht je werkwijze toe. |
| |
|
|
| |
Elke iso-afstandslijn
bestaat uit drie cirkelbogen. Deze drie bogen sluiten op elkaar
aan in de punten L (links) en R(rechts)
Voor alle punten L geldt:
LM + LE = 9. |
| |
|
|
| |
b. |
Toon dit aan |
| |
|
|
|
| |
|
|
|
 |
 |