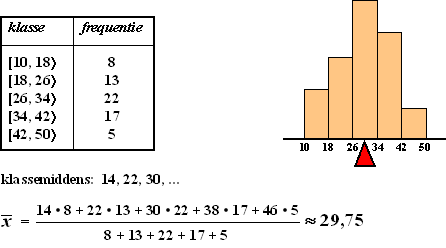centrummaten


Centrummaten.	© h.hofstede (h.hofstede@hogeland.nl)

Naast mooie plaatjes maken willen wij als wiskundigen ook graag metingen samenvatten in getallen. Bij een frequentieverdeling (tabel, histogram, polygoon enz.) vinden we in het algemeen twee dingen interessant.
Op de eerste plaats willen we graag weten waar het midden van de metingen zit. Dat geeft immers aan hoe groot de metingen ongeveer zijn.
Op de tweede plaats willen we weten hoe ver de metingen zo'n beetje van dat midden afliggen. Ofwel: hoe ver de metingen uit elkaar liggen; hoe groot de spreiding in de metingen is.

Om het "MIDDEN" van een serie metingen aan te geven zijn er drie mogelijke manieren. Die heten de centrummaten en we zullen ze één voor één bespreken.

1. Het Gemiddelde.

Nou, die kent iedereen natuurlijk wel. Gewoon alle getallen optellen en dan delen door hoeveel het er waren.
Bij een klassenindeling dan doe je gewoon alsof alle metingen in een klasse gelijk zijn aan het klassenmidden (kijk goed uit wát dat klassenmidden is!). Je krijgt dan een schatting voor het gemiddelde, het werkelijke gemiddelde is niet precies bekend natuurlijk, want je weet niet hoe de metingen wérkelijk over de klassen verdeeld waren.
Het teken dat we gebruiken voor het gemiddelde is een x met een streepje erboven.

voorbeeld 1.

Rechts zie je nog wat je je zo'n beetje voor kunt stellen bij het gemiddelde. Als je histogram gemaakt zou zijn van houten blokken is het gemiddelde het punt ten opzichte waarvan het hele histogram in evenwicht is.

2. De Mediaan.

De mediaan is gewoon het middelste getal van al je metingen.
Daarvoor moet je ze dus wel eerst op volgorde van klein naar groot zetten. Denk er goed om dat het middelste van 10 getallen niet nummer 5 is!!! Die middelste zit tussen nummer 5 en nummer 6 in. In zo'n geval nemen we als mediaan het gemiddelde van de twee getallen waartussen het middelste getal zit.
Bij n getallen is de mediaan nummer ^{(n
+ 1)}/₂Het is in het histogram dus het punt vanwaar de oppervlakte aan beide kanten gelijk is,
voorbeeld 2.
Wat is de mediaan van de getallen 3 - 3 - 4 - 4 - 4 - 4 - 5 - 6 - 6 - 7 - 8 - 8 - 10 - 10 - 10 - 10 - 10 - 14 ?
Er staan hier 18 getallen op volgorde. De middelste daarvan ligt tussen nummer 9 en nummer 10.
Nummer 9 is 6, en nummer 10 is 7, dus de mediaan is 6,5.

Mediaan bij klassenindeling.
Als je te maken hebt met een klassenindeling, en een continue variabele, dan doe je alsof al je waarnemingen gelijkmatig over de klassen verdeeld zijn.

Voorbeeld 3.

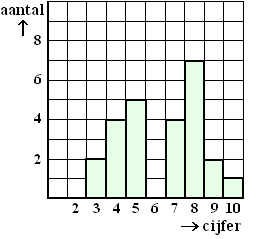
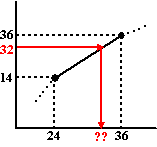
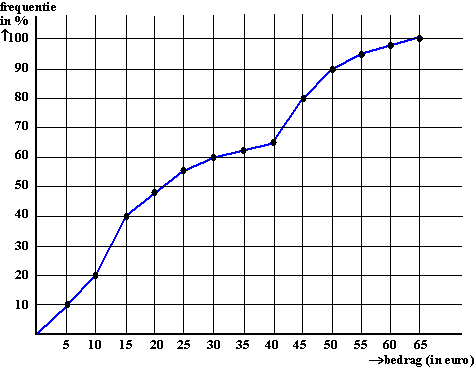
Bepaal de mediaan van de verdeling hiernaast.
de mediaan is de middelste van 63 getallen, dus nummer 32.
Die zit ergens in de klasse 24-<36, maar dichter bij 36 dan bij 24. Waar precies kun je het beste zien in het cumulatieve frequentiepolygoon. Als we daarin inzoomen op de klasse 24 -<36 dan zien we dit:

klasse	aantal
0 - < 12	4
12 -< 24	10
24 -< 36	22
36 -< 48	18
48 -< 60	9

De zwarte stippen staan bij de rechter klassengrenzen. Door te interpoleren kunnen we waarde van de rode vraagtekens vinden:
• van 14 naar 32 is 18 van de totale klassenbreedte 22, dus dat is ¹⁸/₂₂ ste deel.
• dan is van 24 tot de rode vraagtekens ook ¹⁸/₂₂ van de totale breedte 12, en dat is 9,8
• de mediaan is daarom 24 + 9,8 = 33,8.

N.B. Bij een oneven aantal discrete getallen is de Mediaan de middelste daarvan. Bij het berekenen van het 1^e en het 2^e kwartiel tel je die mediaan NIET meer mee voor de aantallen van beide helften.
Als er bijvoorbeeld 15 getallen zijn, is de mediaan nummer 8
De linkerhelft zijn dan 7 getallen dus het eerste kwartiel is nummer 4.

3. De Modus.

De modus is de meest voorkomende meetwaarde, ofwel gewoon het hoogste staafje in het histogram.
Als het om een hele klasse gaat, dan spreken we niet van modus maar van modale klasse.
Als er meerdere metingen of klassen samen de hoogste frequentie hebben, dan is er geen modus of modale klasse aan te wijzen.

In voorbeeld 1 hierboven is de modale klasse [26, 34], en in voorbeeld 2 is de modus 10, en in voorbeeld 3 is de modale klasse 24 -<36.

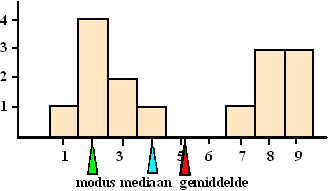
Hier zie je nog in één plaatje de drie centrummaten bij één histogram:

• gemiddelde: punt van "evenwicht"
• mediaan: beide kanten zelfde oppervlakte
• modus: hoogste staaf.

Voor- en Nadelen.

Het gemiddelde lijkt een erg betrouwbare en precieze maat voor het midden, maar soms valt dat tegen. Dat is vooral zo als er sprake is van uitschieters.

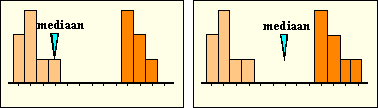
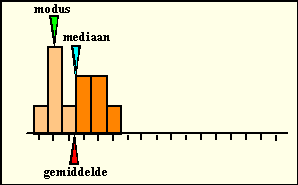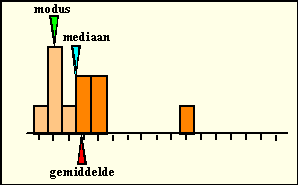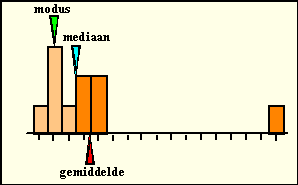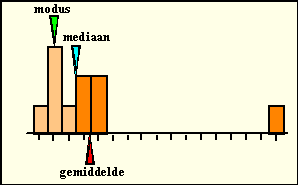
Neem bijvoorbeeld het histogram hiernaast. Daar zie je dat, als er één meetwaarde verandert, ook meteen het gemiddelde mee gaat veranderen, terwijl modus en mediaan gelijk blijven.

De mediaan is veel stabieler.
Eén extra meting of één foute meting zal de mediaan nooit veel kunnen laten verschuiven. Behalve misschien in een verdeling als hieronder, daar verspringt de mediaan ineens als er rechts één meetwaarde bijkomt. Maar goed, dat is wel érg toevallig natuurlijk!

De modus is ook vaak redelijk onbetrouwbaar. Als er meerdere meetwaarden zijn die ver van elkaar af liggen, maar ongeveer even vaak voorkomen, dan kan de modus maar zo van de één naar de ander springen.

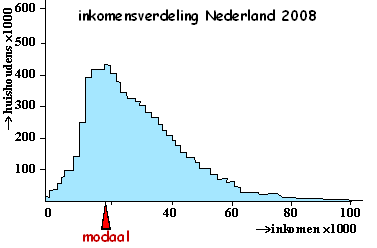
Vooral bij verdelingen met één waarde die verreweg het meest voorkomt is de modus wél een redelijk stabiel getal. Een heel bekend voorbeeld is het modale inkomen.

Hiernaast zie je dat dat in Nederland in 2008 ongeveer
€16000- €18000 was. Maar omdat deze verdeling rechtsscheef is, zal dat beslist niet gelijk zijn aan het gemiddelde inkomen.
Een mooie animatie hiervan is te zien op:

http://www.cbs.nl/nl-NL/menu/themas/inkomen-bestedingen/cijfers/extra/2008-inkomensverdeling.htm

Met de TI-83

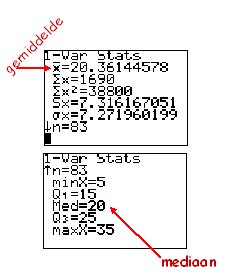
Met de TI-83 kun je gemiddelde en mediaan als volgt bepalen.
Voer eerst je frequentietabel in via STAT - EDIT zoals je al gewend was (klassenmiddens bij L1, frequenties bij L2).
Gebruik dan STAT - CALC - 1: 1-Var Stats
Toets daarachter in ( L1 , L2 )

Dan krijg je het scherm hiernaast en kun je het gemiddelde (x) en de mediaan (Med) aflezen. In dit geval was het gemiddelde gelijk aan 20,36 en de mediaan was 20.

De modus kun je niet vinden op de TI, maar die is dan ook wel érg makkelijk direct uit je tabel af te lezen!!!


cumulatief frequentiepolygoon			spreidingsbreedte, kwartielafstand

Hieronder staat het aantal ogen dat met een dobbelsteen is gegooid.
Bepaal van deze frequentieverdeling de modus, de mediaan en het gemiddelde.

aantal ogen	1	2	3	4	5	6
frequentie	12	16	10	8	19	13

modus 5
mediaan 4
gemiddelde 3,577

Hieronder staat een frequentieverdeling van de spanwijdte van een aantal koolmezen zoals een bioloog die heeft gemeten.

spanwijdte (cm)	19,5 -< 20,0	20-<20,5	20,5 - < 21,0	21,0 -< 21,5	21,5 -< 22,0	22,0 -<22,5	22,5 -< 23,0
frequentie	14	28	56	32	10	6	1

Bereken gemiddelde en modale klasse

20,81 en
21,0 - 21,5

Bepaal zo goed mogelijk de mediaan.

≈20,78

Van iemand die griep heeft verdwijnen de verschijnselen (koorts, rillingen, keelpijn, spierpijn) zo ongeveer na 2 tot 7 dagen. Voor een aantal grieppatiënten is bijgehouden hoe lang de koorts duurde.

aantal dagen	2	3	4	5	6 of meer
aantal patiënten (%)	15	43	22	12	8

Stel dat de laatste groep 6,5 zou zijn in plaats van 6 of meer.
Bereken in dat geval de modus, de mediaan en het gemiddelde.

3, 4 , 3.65

Welk van de drie berekende getallen uit de vorige vraag zou veranderen als er in plaats van "6 of meer" ook 6, 7, 8 enz zou hebben gestaan?

gemiddelde

Welk getal moet er op de plaats van 6 of meer staan als het werkelijke gemiddelde gelijk blijkt te zijn aan 3,75?

7,55

In de tabel hieronder zie je de frequentieverdeling van het aantal uren van de docenten van het Hogeland College.

klasse	10-14	15-19	20-24	25-29
frequentie	18	8	41	9

Wat is het grootst mogelijke gemiddelde bij deze frequentieverdeling? En wat is het kleinst mogelijke gemiddelde?

17,7 en 21,7

De conciërge Tjasse kent van alle docenten de precieze aantallen uren. Hij beweert dat de modus 8 is. Waarom kan dat niet kloppen?

Het staafdiagram hiernaast geeft de rapportcijfers van een klas weer.

Hoeveel leerlingen zaten er naar aanleiding van deze gegevens in deze klas?

Geef het gemiddelde van de cijfers van deze klas.

6,36 en 2,02

De leraar is echter vergeten de zessen erbij te zetten! Hij beweert dat het gemiddelde een 6,3 was.

Hoeveel zessen zijn er geweest als dat klopt?

Hieronder staat een cumulatief frequentiepolygoon. Het is gemaakt naar aanleiding van de gegevens van klanten van Albert Hein. Er staat in aangegeven voor hoeveel euro men boodschappen deed.

Lees uit deze figuur de mediaan af.

≈22

Lees uit deze figuur de modale klasse af.

10 - 15

Bepaal met deze figuur het gemiddelde. Rond af op hele euro's

≈26

Een klas krijgt de resultaten van een proefwerk wiskunde terug. De meisjes scoorden gemiddeld 8,5.
De jongens scoorden gemiddeld 7,6.
Het gemiddelde van de hele klas is 8,0.
Er zitten 12 meisjes in de klas.
Hoeveel leerlingen zitten er in totaal in de klas?

Joris, Michel en Koen doen mee aan een hardloopwedstrijd.
Joris eindigt als eerste van de drie, en hij is precies de middelste van alle deelnemers.
Michel eindigt als 10^e, en Koen als 16^e.

Hoeveel deelnemers waren er?

We hebben de getallen 3, 6, 9, 10.
Welk getal zou je er aan toe kunnen voegen zodat het gemiddelde gelijk wordt aan de mediaan?
Geef alle mogelijkheden.

2, 7, 17

10.

Als een biljarter het heeft over zijn gemiddelde (hij noemt dat trouwens zijn "moyenne") dan bedoelt hij het gemiddeld aantal punten (die noemt hij trouwens "caramboles") dat hij maakt bij één beurt.
Een beurt gaat als volgt: De biljarter probeert een punt te halen. Als dat mislukt is de beurt afgelopen.
Als het lukt mag hij doorgaan en proberen nóg een punt te halen.
Dat gaat net zolang door totdat hij mist.

Dan is zijn beurt voorbij.

Neem aan dat de kans dat een biljarter een punt haalt elke keer hetzelfde is.

Als een biljarter een gemiddelde van 0,8 haalt, hoe groot is dan elke keer de kans dat hij een punt maakt?

⁴/₉

Een ervaren biljarter ontwikkelt de formule p = ^g/_{(g + 1)}

Leg uit dat deze formule klopt.

Als een biljarter een kans van 0,8 heeft om een punt te maken, hoe groot zal dan zijn gemiddelde zijn?

11.

Klas A4A (20 leerlingen) had op het wiskundeproefwerk gemiddeld een 6,2.
Klas A4B (28 leerlingen) had op het wiskundeproefwerk gemiddeld een 6,0.
Klas A4C (15 leerlingen) had op het wiskundeproefwerk gemiddeld een 5,4.

Wat was het gemiddelde van alle drie de klassen samen?

5,92

Wat zou klas A4D (25 leerlingen) gemiddeld moeten scoren om het gemiddelde van alle vier de klassen een 6,0 te laten worden?

7,4

12.

Gegeven is de volgende frequentieverdeling van de leeftijden van leden van een voetbalvereniging:

leeftijd	6 - 10	11 - 15	16 - 20	21 - 25	26 - 30	31 - 35	36 - 40	41 - 45
aantal	24	45	60	32	26	24	10	4

Bereken voor de leeftijden van deze vereniging modus, mediaan en gemiddelde.

16-20
16-20
21,23

Omdat er een klassenindeling is gemaakt kun je niet het precieze gemiddelde weten.

Tussen welke grenzen moet het gemiddelde liggen?

18,73 - 23,73

Het werkelijke gemiddelde blijkt gelijk te zijn aan precies 20. Als we alleen de 75 vrouwen van de vereniging bekijken is hun gemiddelde leeftijd 18.

Hoe groot is de gemiddelde leeftijd van de mannen?

21,85

Zo, en nu nog een paar hele lastigen voor de echte liefhebbers. Hersenkrakers!!!.

13.

101 knikkers, genummerd van 1 tm 101 worden over twee vazen A en B verdeeld.
Knikker nummer 40 blijkt in vaas A te zitten.
Als we deze knikker van vaas A in vaas B doen, dan stijgt het gemiddelde van de nummers in beide vazen met ¹/₄.

Hoeveel knikkers zaten er oorspronkelijk in vaas A?

14.

Vijf leden van een basketbalteam worden gewogen.
Na elke weging wordt het gemiddelde tot dan toe uitgerekend.
Dat gemiddelde blijkt elke keer één kg groter te worden.

Hoe groot is het verschil in gewicht tussen de lichtste en de zwaarste speler?

8 kg

15.

Wiskunde-Olympiade-opgave!!

Alle leerlingen van A5A en van A5B nemen deel aan een zelfde examen. In de tabel hieronder worden de gemiddelde resultaten weergegeven voor de jongens, voor de meisjes en voor de jongens en meisjes gezamenlijk en dit zowel voor A5A als voor A5B. Ook vinden we er het gemiddelde resultaat voor de jongens van beide klassen gezamenlijk. Wat is het gemiddelde resultaat voor de meisjes over de twee klassen tezamen?

	A5A	A5B	A5A en A5B
jongens	71	81	79
meisjes	76	90	?
jongens en meisjes	74	84

Statistiek is niet altijd de juiste oplossing.....

"En, wat was uw vonnis?"

"Ik kon kiezen uit 100 jaar of levenslang"

"En wat heeft u gekozen?"

"Nou ja, levenslang natuurlijk, statistisch gesproken is dat korter dan 100 jaar!!!"