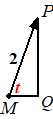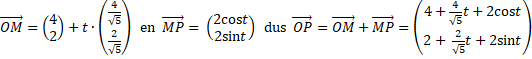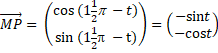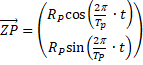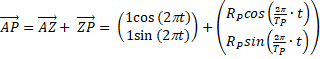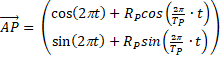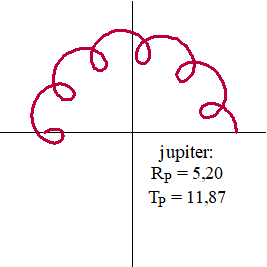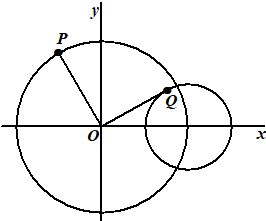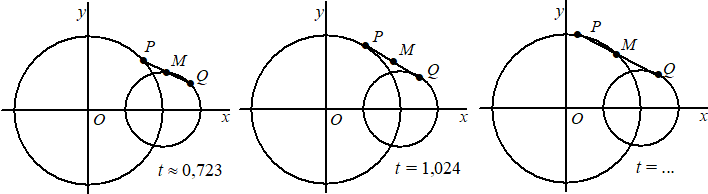vorm van een baan

© h.hofstede (h.hofstede@hogeland.nl)

Bewegende Vectoren.

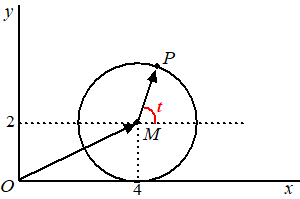
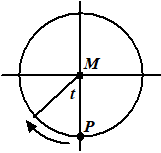
Deze les gaan we vectoren bekijken die bewegen.

Laten we starten met een cirkel met middelpunt M(4, 2) en straal 2 en een punt P dat ergens op die cirkel ligt, met een hoek t zoals aangegeven in de figuur.

Laten we beide vectoren in de figuur hiernaast bekijken.

We zoomen in op vector MP:

MP = 2 want dat is de straal van de cirkel. Teken punt Q met een rechte hoek MQP.
Dan geeft sos-cas-toa: MQ = 2cost en MP = 2sint. En dat zijn precies de kentallen van vector MP, dus:

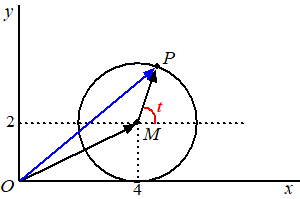
En dan kunnen we natuurlijk meteen de vector OP bekijken:

Kijk nu eens naar wat er gebeurt als we t veranderen. Dan komt punt P steeds op een andere plaats op de cirkel te liggen, maar het hele verhaal hierboven blijft gelden, dus die vector OP blijft de kentallen hierboven houden. Als t verandert beweegt vector OP mee met de plaats van P op de cirkel.
En als je voor t de tijd kiest dan heb je een punt P dat rondjes om de cirkel loopt.

Eén omwenteling kost dan 2π seconden, en als we hokjes van 1 cm nemen dan is de omtrek 4π cm. Dus de snelheid van P is 2 cm/sec.

Oké, tot nu toe is het voorbeeld nogal makkelijk (waarschijnlijk had je ook wel direct de coördinaten van P(4 + 2cost, 2 + 2sint) kunnen opschrijven), maar het was dan ook vooral bedoeld om de aanpak te demonstreren.

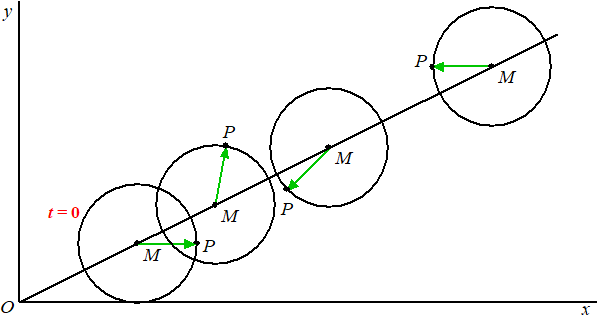
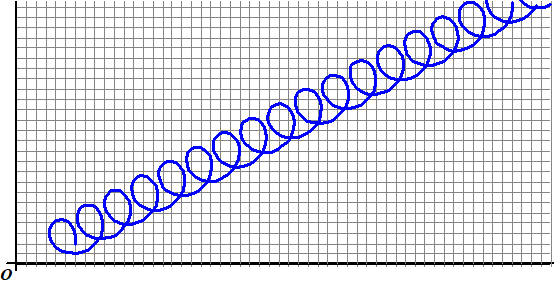
Weet je wat? Laten we de zaak wat boeiender maken door punt M ook te laten bewegen! We laten M langs de lijn y = ¹/₂x omhoog lopen, en intussen blijft punt P zijn rondjes rond de cirkel draaien, zoiets dus:

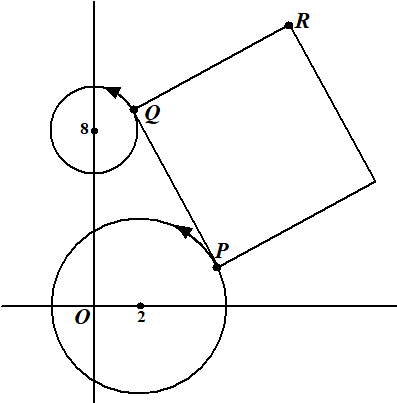
Op vier tijdstippen is de cirkel met middelpunt M op de lijn y = ¹/₂x getekend en punt P op die cirkel.
Wat voor vreemde kronkelbeweging maakt P nu?

Om die vraag te beantwoorden zullen we eerst moeten kiezen met welke snelheid M over die lijn beweegt.
Omdat de richtingscoëfficiënt van OM gelijk is aan ¹/₂ kunnen we een vectorvoorstelling van OM opstellen:

We hebben als de steunvector de plaats van M op t = 0 gekozen.

voorbeeldsnelheid nr.1.
Je zou simpelweg kunnen zeggen: we nemen λ = t
Als t dan met 1 toeneemt, schuift de plaats van M op de lijn één richtingsvector op. Die heeft lengte √5, dus in dit eerste geval heeft M een snelheid van √5 cm/sec.
Dat zou geven:

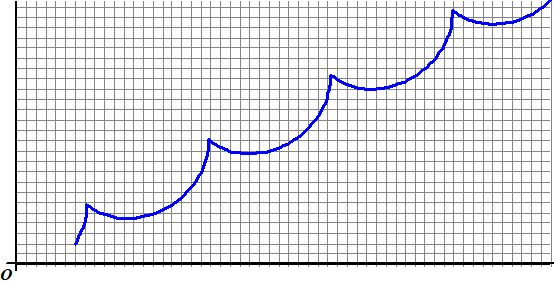
En de baan van P zou er zó uitzien (ik leg straks uit hoe je deze plaatjes zelf kunt maken):

voorbeeldsnelheid nr. 2.
Je zou ook kunnen zeggen: "ik wil dat M met snelheid 2 cm/sec over de lijn loopt" (de snelheid waarmee P om M draait).
Dan moet je ervoor zorgen dat de richtingsvector lengte 2 krijgt (want als t dan 1 toeneemt, verschuift M over afstand 2)
Die vector had lengte √5, dus die moet je vermenigvuldigen met ²/_√5.
Dat geeft:

en dan ziet de baan van P er zó uit:

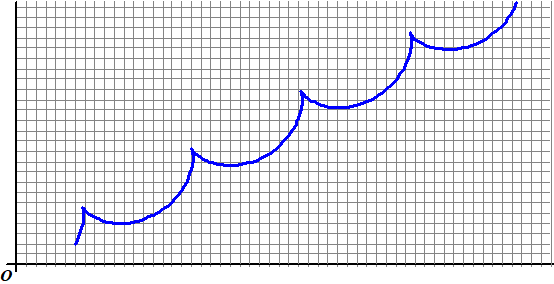
Lijkt nogal op de vorige, iets meer "in elkaar gedrukt".

voorbeeldsnelheid 3.
Laten we de snelheid van M eens heel klein nemen. Bijvoorbeeld 0,5 cm/sec.
Dan moet die richtingsvector lengte 0,5 krijgen, dus vermenigvuldigen met ^0,5/_√5, en dat geeft:

Tussendoortje.

Als je de x-coördinaat en de y-coördinaat van punt P apart als een vergelijking met t geeft, dan krijg je een zogenaamde parametervoorstelling.
Het allereerste voorbeeld hierboven zou er dan zó uitzien:

In de J-lessen van deze lessenserie worden de eigenschappen van parametervoorstellingen uitgebreid behandeld.
Daar staat eigenlijk hetzelfde als in deze vectorlessen.
In deze les kun je direct al vinden hoe je de plaatjes hierboven zelf met je GR kunt maken.

Twee bekende voorbeelden.

voorbeeld 1: de cycloïde.

Als een wiel met straal 1 en snelheid 1 over een vlak oppervlak rolt, dan beschrijft een punt op de omtrek van dat wiel een parameterkromme die cycloïde heet. Dat ziet er ongeveer zó uit (de rode lijn):

Met vectoren is die baan erg eenvoudig te beschrijven.

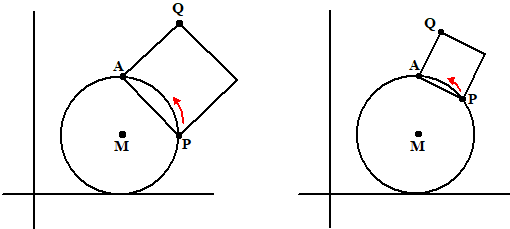
Noem het middelpunt van de cirkel M en laat punt P onderaan beginnen.
Als de cirkel met de klok meedraait (laat M zolang op dezelfde plaats blijven) dan is dat net alsof punt P met de klok mee om M draait. Zie de figuur hiernaast.

Omdat M met snelheid 1 naar rechts beweegt legt M in 1 seconden ook 1 cm af, dus in 2π seconden legt M precies de omtrek van de cirkel af, en is P dus precies één keer rondgedraaid. De periode van de draaiing van P om M is daarom precies 2π.

Verder beweegt M met snelheid 1 naar rechts, dus legt in t seconden t cm af, dus:

voorbeeld 2: planeetbewegingen.

Al in 1514 stelde de Poolse priester Nicholas Copernicus dat een erg simpel model van het zonnestelsel zou zijn dat de zon in het midden staat en dat de planeten eromheen draaiden. "Heliocentrisme" werd dat genoemd.
Het duurde bijna een eeuw voordat zijn idee serieus genomen werd. Toen begonnen eindelijk twee astronomen, Johannes Kepler en Gallileo Galileï, openbaar dit idee te steunen.
Daar was de kerk het niet mee eens, want die hadden liever dat de aarde het middelpunt van alles was. (in Prediker 1:5 staat bijvoorbeeld letterlijk dat de zon op en onder gaat). Het kwam zelfs in 1610 tot een proces waarin de inquisitie Galileï veroordeeld voor "heliocentrism". Dat werd vanaf toen officieel als "ketterij" beschouwd.v Galileï kreeg een waarschuwing.

Maar Galileï ging gewoon door. Hij ontdekte door zijn betere telescopen dat er manen om Jupiter draaien. Hij verklaarde met het model de getijdenbeweging.

In 1632 schreef Galileï "Dialogo sopra i due massimi sistemi del mondo". In het boek discussiëren drie personen , Salviati, Sagredo en Simplicio, met elkaar. Daarbij vertegenwoordigde Salviati het heliocentrische model, en Simplicio vertegenwoordigde het oude model met de aarde in het middelpunt. Simplicio verloor de discussie uiteraard overtuigend, en maakte aan het eind een aantal opmerkingen van de paus.
De paus werd duidelijk belachelijk gemaakt, was woedend, en liet een nieuw onderzoek naar Galileï instellen.
Daarbij werd Galileï (intussen een oude man van 69) uiteraard schuldig aan ketterij bevonden en werd veroordeeld tot levenslang huisarrest.

Toch was dat wel een beetje eigenwijs van de inquisitie.....

Hoe eigenwijs???

Stel dat inderdaad de aarde in het midden staat en dat de zon en de andere planeten er omheen draaien......
Laten we proberen een (vereenvoudigd) idee te krijgen van wat voor planeetbewegingen dat zou opleveren.

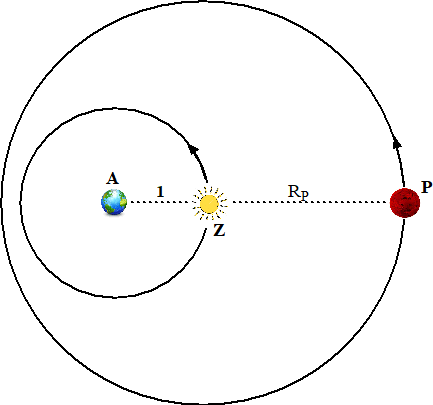
Stel dat de beginsituatie is zoals hierboven (t = 0)
De afstand Aarde-Zon noemen we 1 (in werkelijkheid 1AE = 150 miljoen km). Dus we doen alsof de zon om de aarde draait met een omlooptijd van 1 (jaar) op afstand 1 (AE). Wat zou dat voor vector AP opleveren?

We weten dat de planeet om de zon draait op afstand R_P (in AE gemeten) en met omlooptijd T_P (in aardse jaren)
Dus:

Dus dan geldt:

ofwel:

Deze vector beschrijft hoe de planeet P beweegt om de aarde, die in het middelpunt staat.
Nou, maar eens kijken wat dat voor een paar planeten zou opleveren:

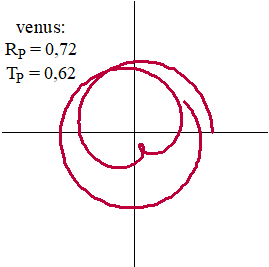
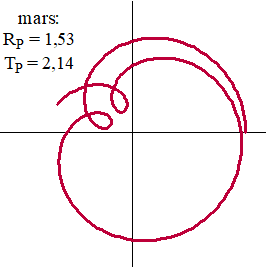
In plaats van eenvoudige cirkelbewegingen rondom de zon (waarvan Kepler trouwens aantoonde dat het ellipsen zijn) zouden de planeten deze vreemde bewegingen rond de aarde maken. Waarom? Tja....

Je zou je letterlijk in allerlei bochten moeten wringen om dit vreemde planeetgedrag te verklaren.

nawoord.
In oktober 1992 sprak paus Johannes Paulus II een excuus uit, waarmee Galilei's naam werd gezuiverd en Galilei werd erkend als gelovig mens. In 2008 waren er in het Vaticaan zelfs plannen om de rehabilitatie van Galilei kracht bij te zetten door een beeld van hem binnen de muren van Vaticaanstad te plaatsen. Paus Benedictus XVI prees dat jaar ook Galilei's grote bijdrage aan de sterrenkunde.
Een jaar later besloot men het beeld toch maar niet te plaatsen......... jammer........!


OPGAVEN.

1.	c is de cirkel met middelpunt M = (3, 2) en straal r = 2. Punt P volgt een baan langs deze cirkel c met omlooptijd 2π, en begint op t = 0 rechts van M. Punt A is het vaste punt (3, 4). AP is een zijde van een vierkant waarvan Q het punt tegenover P is. Zie de figuur, waarin op twee momenten de situatie is weergegeven.





	a.	Toon dat aan, en geef een formule voor de oppervlakte van het vierkant als functie van t. Schrijf je antwoord zo eenvoudig mogelijk.

	b.	Geef een parametervoorstelling voor de baan van Q en leg duidelijk uit hoe die baan eruit ziet en waarom dat zo is.

2.	Punt P beweegt over een cirkel met middelpunt (2,0) en straal 3 Punt Q beweegt over een cirkel met middelpunt (0,8) en straal 2 Beide punten hebben dezelfde omlooptijd. Zie de figuur.



	R is het hoekpunt van een vierkant met zijde PQ, zoals in de figuur. Stel een parametervoorstelling op voor punt R.

3.	Examenvraagstuk VWO wiskunde B, 2022 - II

	Voor 0 ≤ t ≤ 2π beweegt een punt P over een cirkelvormige baan c_P met middelpunt O(0, 0) volgens de bewegingsvergelijkingen:


	Voor 0 ≤ t ≤ 2π beweegt tegelijkertijd een punt Q over een cirkelvormige baan c_Q volgens de bewegingsvergelijkingen:


	Hoek POQ is afhankelijk van t. In de figuur zijn beide cirkels c_P en c_Q weergegeven. Ook zijn de lijnstukken OP en OQ weergegeven voor een waarde van t waarvoor OP en OQ loodrecht op elkaar staan.

	a.	Bereken exact de waarden van t waarvoor OP en OQ loodrecht op elkaar staan

	De lijn door P en Q snijdt de x-as in punt A. De x-coördinaat van A is onafhankelijk van t.

	b.	Bewijs dit.

	Punt M is het midden van lijnstuk PQ. Op t = 0 beginnen P en Q vanaf de x-as naar boven te bewegen. Punt M beweegt dan mee naar boven. In de volgende figuren is voor drie waarden van t de situatie weergegeven.



	Voor t ≈ 0,723 ligt punt M op cirkel c_Q. Zie de linkerfiguur. Na t ≈ 0,723 komt M in het gebied buiten c_Q te liggen. Zie de middelste figuur. Op een zeker tijdstip ligt M op cirkel c_P. Zie de rechterfiguur. Punt M ligt een percentage van de tijd waarin de punten P en Q een volledige baan doorlopen buiten c_P en c_Q.

	c.	Bereken dit percentage. Geef je eindantwoord als geheel getal.