parameterkrommen

© h.hofstede (h.hofstede@hogeland.nl)

Wat is een parameterkromme?

Kijk goed naar de plaat hiernaast.
Dit soort puzzels ken je vast nog wel van achter in de auto vroeger . Zo'n prachtig "Vakantieboek" van toen je nog op de basisschool zat.

Nou, ik zal je zeggen, dat verbinden van die punten met lijntjes wat wij als kleuter al deden, dat is eigenlijk het basisidee achter wat wiskundigen noemen een "parameterkromme".

Het is een andere manier om grafieken en krommen te tekenen. Er is nog steeds een x-as en een y-as zoals we gewend zijn, maar de getallen die bij de stippen van de tekening staan hebben ook een naam. We gebruiken er een derde letter voor, meestal t. Er is geen gewone vergelijking of formule tussen x en y, nee, deze keer worden x en y beiden uitgerekend via deze t:

Alles loopt via t

Laten we een typisch voorbeeld bekijken:

Gegeven is de kromme K door:

Laten we gewoon een heleboel t-waarden nemen en de bijbehorende x en y uitrekenen met deze twee formules:

t	0	¹/₆π	¹/₄π	¹/₃π	¹/₂π	³/₄π	π	1¹/₆π	1¹/₄π	1¹/₃π	1¹/₂π	1³/₄π	2π
x	0	√3	2	√3	0	-2	0	√3	2	√3	0	-2	0
y	-1	0	0,52	1	√3	1,93	1	0	-0,52	-1	-√3	-1.93	-1

Teken nu deze (x,y) waarden als stippen en zet de bijbehorende waarde van t erbij.
Dat geeft de figuur hiernaast.

En zie!
Daar is onze vakantieboekpuzzel al!
Verbind de punten met elkaar en je krijgt de volgende kromme:

Met de GR.

Al dit werk kan de TI-83 ook voor ons doen.......
Zet hem op MODE - Par.
Met Y = krijg je nu X1T = en Y1T = in beeld.
Daar voer je de formules voor x en y in (waarbij de t nu de knop X,T,θ,n is)
Met WINDOW kun je nu de x- y- én t-grenzen instellen.
Dat geeft het volgende resultaat.

1.	Schets de volgende parameterkrommen:

	a.	x(t) = 4cos(t) en y(t) = sin(t)
	b.	x(t) = t + cos(2t) en y(t) = t + sin(3t)
	c.	x(t) = (1 + cos(3t)) • cos(t) en y(t) = (1 + cos(3t)) • sin(t)


2.	Hieronder staan een x(t) en een y(t) grafiek getekend. Schets de bijbehorende parameterkromme.



3.	Een erg beroemde parametervergelijking is de "vlinder", ontdekt door Fay in 1989. Probeer hem maar eens te plotten, 't is niet makkelijk...

	Wauw!! Zo moeilijk zullen wij ze maar niet verder bestuderen.

4.	Hieronder staan de grafieken van x(t) en y(t). Schets de bijbehorende parameterkromme.



5.	Het is in school 's morgens vroeg erg vaak erg warm. Juist als het buiten koud is. Hoe komt dat toch? Het ligt aan de thermostaat. Stel dat die staat ingesteld op 20°C. Zodra de lokaaltemperatuur dan zakt onder de 20° dan slaat de ketel aan en wordt het water in de radiatoren warmer en warmer. Maar dat gaat langzaam, dus eerst zakt de temperatuur in het lokaal nog verder. Pas als de radiator warm genoeg is wordt het lokaal ook langzaam warmer. Als het lokaal weer 20° is geworden, dan slaat de ketel af en wordt het radiatorwater niet meer verwarmd . Maar het radiatorwater is op dat moment zo warm dat het lokaal nog een poosje doorverwarmd wordt. En zo komt het dat de lokaaltemperatuur schommelt. De volgende formules blijken te gelden:


	Daarin is L de lokaaltemperatuur, R de radiatortemperatuur, en t de tijd in minuten.

	a.	Teken de kromme waarin L (op de x-as) is uitgezet tegen R(op de y-as)

	b.	Op een gegeven moment is de temperatuur van de radiator precies het dubbele van de lokaaltemperatuur. Lees in de figuur uit vraag a) af hoe warm het lokaal op dat moment zou kunnen zijn.

SNIJPUNTEN met de ASSEN

Die zijn erg makkelijk te vinden, zolang je je het volgende maar realiseert:

x - as ⇒ y = 0
y - as ⇒ x = 0

En verder gaat alles uiteraard weer "via t".
Dus voor de snijpunten met de x-as stel je y(t) = 0. Dat los je op, en hopelijk vind je t-waarden.
Die t-waarden vul je in in de vergelijking voor x(t) om de bijbehorende x-waarde van het snijpunt te vinden. En met de y-as gaat het precies zo.

Voorbeeld.
Het voorbeeld aan het begin van deze paragraaf heeft zo te zien één snijpunt met de x-as. Dat vinden we als volgt:
y = 0 ⇒ 2sin(t - ¹/₆π) = 0
⇒ sin(t - ¹/₆π) = 0
⇒ t - ¹/₆π = 0 + k • 2π of t - ¹/₆π = π + k • 2π
⇒ t = ¹/₆π of t = 1¹/₆π
t = ¹/₆π geeft x = 4sin¹/₆π • cos¹/₆π = 4 • ¹/₂ • ¹/₃√3 = ²/₃√3 dus het snijpunt (²/₃√3, 0).
t = 1¹/₆π geeft x = 4sin1¹/₆π • cos1¹/₆π = 4 • -¹/₂ • -¹/₃√3 = ²/₃√3 dus het snijpunt (²/₃√3,0).
Gelukkig maar, want we wisten al dat er maar één snijpunt was....

Het voorbeeld aan het begin van deze paragraaf heeft zo te zien 4 snijpunten met de y-as.
Bereken algebraïsche de coördinaten van deze snijpunten.

(0, ±1) en (0, ±√3)

Gegeven is de parameterkromme: x(t) = 2t -¹/₂t² en y(t) = 2 - ¹/₂t²
Bereken algebraïsch of de snijpunten van deze kromme met de x-as even ver uit elkaar liggen als de snijpunten met de y-as.

ja: afstand 8

Gegeven is de kromme met parametervoorstelling x(t) = ¹/₂t • cos(πt) en y(t) = ¹/₂t • sin(πt)

Plot deze kromme.
Iemand beschrijft deze kromme als "Gewoon een cirkel die steeds groter wordt"
Leg uit hoe je dat zonder te plotten aan de vergelijkingen voor x en y al had kunnen zien.

Toon aan dat de opeenvolgende snijpunten met de positieve y-as op gelijke afstand van elkaar liggen (op de oorsprong na).

Gegeven zijn de parameterkrommen K_p, met p > 0, en -2π ≤ t ≤ 2π:

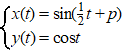Voor elke waarde van p krijg je een andere kromme K. Hieronder staan er een aantal getekend.

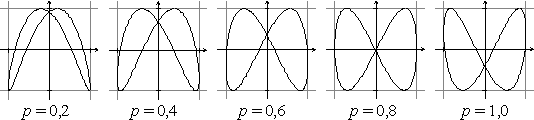
Het lijkt erop dat als p groter wordt, het snijpunt met de y-as langzaam "naar beneden zakt", en dat de middelste twee snijpunten met de x-as naar elkaar toe gaan.

Voor welke p tussen 0 en π is het snijpunt met de y-as het punt (0, ¹/₂√2)?

p = ⁷/₈π

Voor welke p tussen 0 en π vallen de middelste twee snijpunten van deze kromme met de x-as samen?

p = ¹/₂π

10.

Gegeven zijn op t in [0,2π] de volgende drie krommen:

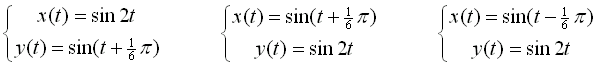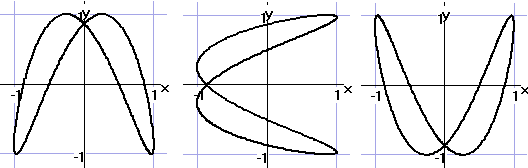
Hieronder zie je drie bijbehorende grafieken.
Zoek zonder de GR te gebruiken uit welke kromme bij welke vergelijkingen hoort. Geef een duidelijke toelichting.