 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
Verhoudingen in rechthoekige driehoeken. |
|
|
Laten we een rechthoekige
driehoek nemen.
Stel dat je de grootte van één van de andere hoeken
daarvan ook kent, bijvoorbeeld de hoek met de rode stip hiernaast.
Dan ken je ook de derde hoek, immers je weet vast nog wel dat de som van de
hoeken van een driehoek gelijk is aan 180º.
| |
| Als je er twee weet, weet
je ze alle drie! |
|
| |
|
 |
| Maar als alle drie de hoeken van een driehoek
bekend zijn, dan zijn er niet zoveel mogelijkheden meer om die driehoek
te tekenen. |
|
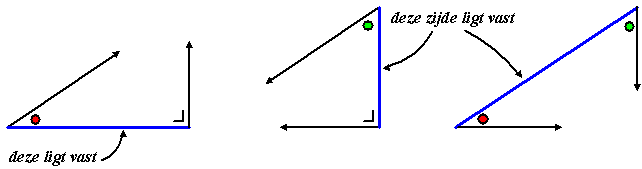
| Zodra je één zijde weet, dan is de
hele driehoek bekend. Kijk maar naar de drie tekeningen hieronder waar
steeds één van de drie zijden "vast" wordt gelegd, en waar steeds alle
drie de hoeken bekend zijn. In alle gevallen is er nog maar één driehoek
mogelijk om te tekenen. Bedenk steeds dat de rechte hoek en de rode en
de groene hoek bekend zijn! |
|
|
|
 |
| |
|
|
Er is steeds maar één driehoek
mogelijk!!! |
|
|
|
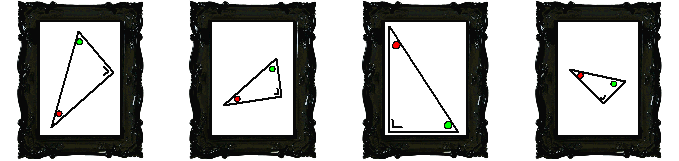
| Eigenlijk zijn al die driehoeken
die je nog kunt tekenen met drie zulke hoeken vergrotingen of
verkleiningen van elkaar. Ze hebben dezelfde vorm, maar het is alsof je
een foto van de driehoek hebt genomen en die daarna hebt vergroot of
verkleind. |
|
|
|
 |
|
|
| Als zulke driehoeken vergrotingen
of verkleiningen van elkaar zijn, dan zijn de verhoudingen
van de lengtes van hun zijden gelijk. Die verhoudingen heten de
goniometrische verhoudingen van een rechthoekige driehoek. |
| |
|
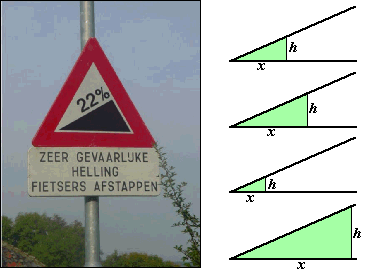
Bij een straat of weg zijn we daar
al aan gewend; daar hebben we vaak te maken met een bepaald
hellingspercentage. Een hellingspercentage van 22% betekent
bijvoorbeeld dat bij elke meter die je horizontaal aflegt, de
weg 0,22 meter stijgt.
Dat betekent in de figuur hiernaast dus dat de verhoudingen van
h en x in alle groene driehoeken rechts gelijk zijn
(namelijk in dit geval h/x =
0,22).
Die verhouding hangt alleen maar af van de hoek die de weg met
een horizontaal vlak maakt.
Bij elke hoek zou je dus alvast die verhouding kunnen
uitrekenen. Dat zou trouwens zo'n soort tabel opleveren: |
 |
| |
|
| hoek |
10º |
20º |
30º |
40º |
50º |
60º |
70º |
80º |
| verhouding h/x |
0,176 |
0,364 |
0,577 |
0,839 |
1,192 |
1,732 |
2,747 |
5,671 |
|
| |
|
| Die verhouding h/x
die bij een hoek hoort heet de tangens van die
hoek, en we noteren hem als tanα
(waarbij
α de hoek is waar
het om gaat). Om je nou een boel werk te besparen zijn tabellen
als hierboven onder een knop van je rekenmachine gepropt, in dit
geval de knop
TAN
. |
|
Probeer maar uit : TAN(30)
geeft inderdaad de verhouding 0,577 uit bovenstaande tabel. (Als dat
niet zo is, dan moet je je rekenmachine eerst instellen op graden; dat
gaat via
MODE -
Degree)
En je rekenmachine kan het ook omgekeerd: voor elke verhouding kun je de
bijbehorende hoek vinden via
SHIFT -
TAN-1
Probeer maar uit dat TAN-1(1,192) inderdaad een
hoek van (ongeveer) 50º oplevert. |
 |
| |
|
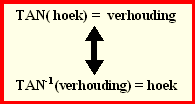
| Hou die twee goed uit elkaar: |
|
 |
| |
|
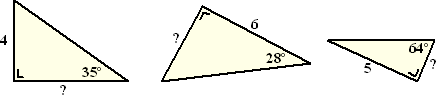
| 1. |
Bereken de vraagtekens in de volgende
driehoeken. |
| |
|
|
|
| |
 |
| |
|
|
|
| 2. |
Bereken de vraagtekens in de volgende
driehoeken. |
| |
|
|
|
| |
 |
| |
|
|
|
| 3. |
Een auto rijdt een berg op over een
weg met een hellingshoek van 8º.
Hoeveel meter is de auto gestegen als hij hemelsbreed 2 km heeft
afgelegd? |
| |
|
|
|
| |
|
|
|
| 4. |
Een vliegtuig daalt onder een hoek van 6°
Hoeveel legt het vliegtuig horizontaal af, als het van een
hoogte 1200 meter naar de grond moet afdalen? |
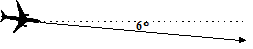 |
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
Nog meer verhoudingen. |
|
|
In het voorafgaande werd steeds
een hoek berekend met behulp van de twee zijden die aan de rechte hoek
grenzen (de rechthoekszijden). Maar natuurlijk kun je net
zo goed de verhouding van twee andere zijden nemen. Van één van die
rechthoekszijden met de schuine zijde dus. Die verhouding ligt net zo
goed vast als de hoeken gegeven zijn! En andersom: als die verhouding
gegeven is liggen de hoeken van de driehoek ook vast.
Die twee andere verhoudingen heten de sinus en de
cosinus van de hoek. Je noteert het als SIN(α)
en COS(α)
Het werkt als volgt: |
|
|
stap 1.
Kijk wat de schuine zijde van de driehoek is. Dat is natuurlijk de
langste, maar als je dat niet goed kunt zien, kun je het veiligst
gebruiken dat het degene tegenover de rechte hoek is. |
|
|
stap 2.
Beslis om welke hoek het gaat. Dus de hoek die je wilt berekenen of een
hoek die gegeven is (als je een lengte wilt berekenen). |
|
|
stap 3.
De schuine zijde heb je al. Dan zijn er nog twee rechthoekszijden over.
Degene daarvan die aan jouw hoek vastzit noem je de aanliggende
rechthoekszijde, en degene tegenover jouw hoek heet de
overstaande rechthoekszijde. |
| |
|
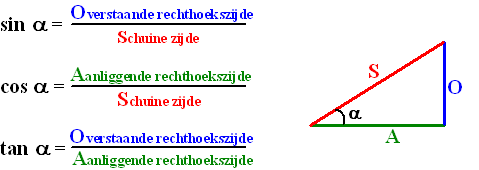
stap 4.
Nu geldt: |
|
|
 |
|
|
Om dit allemaal wat makkelijker te
onthouden is het ezelsbruggetje SOS - CAS - TOA misschien handig.
SOS van "Sinus-Overstaand-Schuin", CAS van "Cosinus-Aanliggend-Schuin"
en TOA van "Tangens-Overstaand-Aanliggend".
Zeg nu eerst om te oefenen 20 keer hardop dit ezelsbruggetje. |
| |
|
|
 |
| |
|
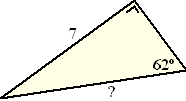
Voorbeeld 1.
Bereken het vraagteken in de driehoek hiernaast.
Het gaat om de hoek van 62º. De schuine zijde is die met het vraagteken
(tegenover de rechte hoek). De zijde van 7 is dan de overstaande zijde
(tegenover de hoek van 62º)
Het gaat dus om de schuine en de overstaande zijden, dus gebruiken we
SOS.
sin(62º) = 7/? dus ? = 7/sin(62)
≈ 7,93 |
 |
| |
|
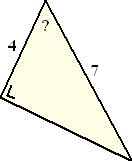
Voorbeeld 2.
Bereken het vraagteken in de driehoek hiernaast.
De zijde van 7 is de schuine zijde (tegenover de rechte hoek). Het gaat
om de hoek met het vraagteken dus de zijde van 4 is dan de aanliggende
zijde.
Met aanliggend en schuin gebruiken we CAS.
cos(?) = 4/7 dus ? = cos-1
(4/7) ≈ 55,2º |
 |
| |
|
|
Zelf een rechte hoek maken.... |
| |
|
Af en toe moet je eerst wat
voorbereidend werk verrichten voordat je SOS-CAS-TOA kunt toepassen. Dat
is vooral zo als er geen driehoek met een rechte hoek is.
Neem de gelijkbenige driehoek links hiernaast. Daarin is geen rechte
hoek te vinden, maar als je de loodlijn vanuit de top tekent wél. Omdat
de driehoek gelijkbenig is deelt die lijn de tophoek en de basiszijde
doormidden.
In een halve driehoek is de schuine zijde 6, en is de x-zijde de
overstaande zijde van de hoek van 14º. Daarom gebruik je SOS.
sin(14º) = x/6 dus x = 6 • sin(14º)
≈ 1,45
Het vraagteken is dan ongeveer 2 • 1,45 = 2,90 |
 |
| |
|
| |
|
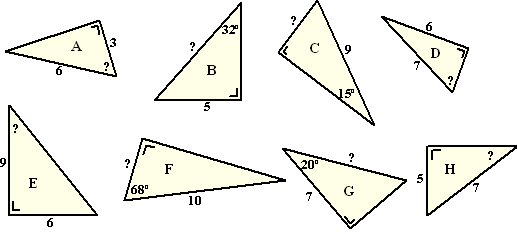
| 5. |
Bereken de vraagtekens in de volgende
driehoeken. |
| |
| |
  |
|
A:60º; B: 9,43; C: 2,33; D: 59º
E: 34º; F: 3,75; G: 7,45; H: 46º |
|
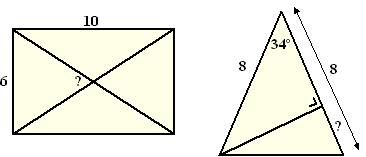
| 6. |
Bereken de vraagtekens in de volgende figuren. |
| |
| |
 |
|
|
| |
|
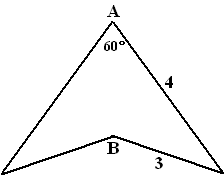
| 7. |
De
pijlpunt hiernaast is symmetrisch in lijn AB.
De afmetingen zijn als in de figuur aangegeven.
Bereken de lengte van AB |
 |
| |
|
|
|
| |
|
|
|
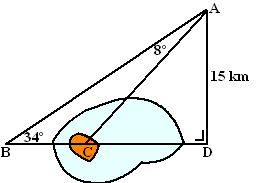
| 8. |
Op
een eiland in een meer ligt een huis C.
Ook in punt B staat een huis.
De afstand BC is zonder boot niet direct te meten.AD = 15 km
De hoeken ABC en CAB zijn gelijk aan 34º en 8º zoals aangegeven.
Hoe ver liggen de huizen B en C van elkaar af? |
 |
| |
|
|
|
| |
|
|
|
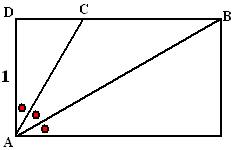
| 9. |
Hoek
A van een rechthoek wordt in drie gelijke delen verdeeld.
AD = 1
Bereken de omtrek van driehoek ABC. |
 |
| |
|
|
|
| |
|
|
|
| 10. |
Ik sta aan de oever van een brede
rivier en wil graag de breedte ervan bepalen. Gelukkig staat er
een boom aan de overkant.
Ik meet vanaf twee punten A en B de
hoek die de oever maakt met de lijn naar de voet C van de
boom.
Dat levert op ∠ABC = 40° en ∠BAC = 60°
Verder meet ik dat de afstand AB gelijk is aan
120 meter.
Hoe breed is de rivier? |
 |
| |
|
|
|
| |
|
|
|
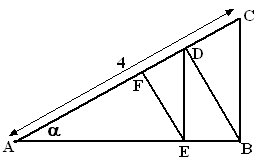
 11. 11. |
In
een rechthoekige driehoek ABC met rechte hoek B is AC = 4.
BD staat loodrecht op AC
DE staat loodrecht op AB
EF staat loodrecht op AC
Toon aan dat EF = 4sinαcos3α |
 |
| |
|
|
|
 |
|
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|