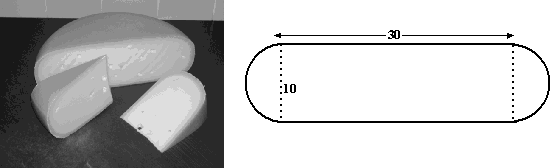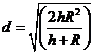|
© h.hofstede (hhofstede@hogeland.nl) |
||||
|
|
Een
motorboot vaart vanaf een schip recht naar het noorden met een snelheid
van 80 km/uur. Intussen vaart het schip naar het zuidoosten met een snelheid van 32 km/uur. De motorboot heeft voor 4 uur brandstof. Hoe ver kan de motorboot maximaal naar het noorden varen om nog weer terug naar het schip te kunnen komen? |
|||
|
||||
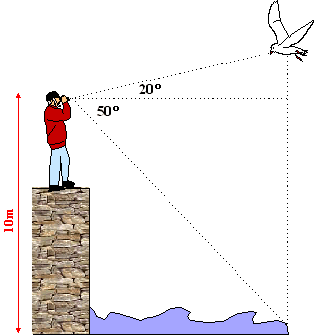
| 2. | Een
ornitholoog bevindt zich op hoogte 10m
boven de
waterspiegel van een meer. Boven zich ziet hij een vogel onder een hoek van 20º en het punt recht onder de vogel op het wateroppervlak ziet hij onder een hoek van 50º Bereken de afstand van de ornitholoog tot de vogel. |
 |
||
|
||||
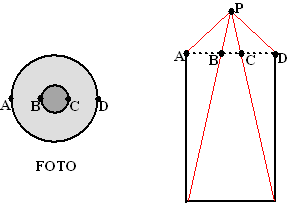
| 3. | In mijn tuin staat een grote
cirkelvormige put. Ik weet niet hoe diep hij is, maar dat wil ik graag
op een wiskundige manier gaan onderzoeken. Ik houd daarom een camera boven het midden van de put in een punt P, 2 meter boven de bovenrand. |
|||
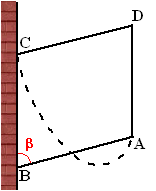
| Een foto van de put ziet er dan
uit als hiernaast. Rechts zie je een zijaanzicht van de situatie. De bovenrand van de put heeft een doorsnede van 3 meter. |
|
|||
| a. | Bereken hoek APD | |||
|
||||
| b. | Op de foto blijkt dat BC = 1/8AD (de tekening klopt niet; is maar een schets). Bereken hoek BPC | |||
|
||||
| c. | Bereken de diepte van de put. | |||
|
||||
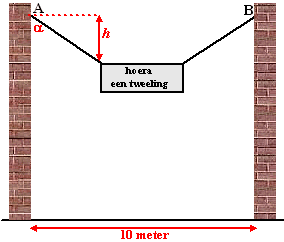
| 4. | Midden boven een 10 meter breed
straatje hangt een spandoek aan een touw dat van A naar B loopt. A en B
liggen op dezelfde hoogte. Het touw is in totaal 14 meter lang. Het spandoek is in totaal 3 meter breed. |
|
||
| a. | Bereken hoek α. | |||
|
||||
| b. | Bereken het hoogteverschil h in twee decimalen nauwkeurig. | |||
|
||||
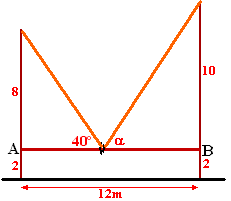
| 5. | Tussen twee palen met hoogten 8m
en 10m is een staaf AB aangebracht met daaromheen een ring. Een elastiek wordt gespannen van de top van de ene paal door de ring naar de top van de andere paal. De ring kan heen en weer bewegen over staaf AB. De horizontale afstand tussen de palen is 12 meter. bereken hoek α als gegeven is dat hoek β = 40º. |
|
||
|
||||
| 6. | Iemand heeft een passer waar hij een cirkel met straal 50 mm mee tekent. De beide benen van de passer zijn 9 cm lang. Bereken de hoek die de benen tijdens het tekenen van de cirkel met elkaar maken. | |||
|
||||
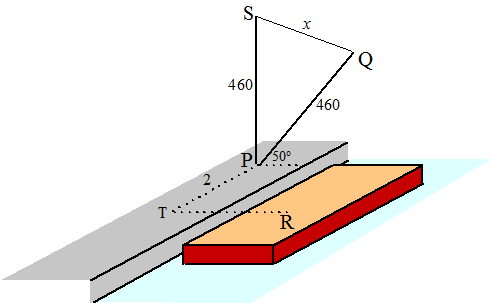
| 7. | Om schepen in de haven te laden of te lossen wordt vaak gebruik gemaakt van een laadboom. Zie de volgende figuur. | |||
|
|
||||
| SP is een loodrecht op de bodem
staande mast van 4,60 meter lang. Daaraan vast in punt P zit een tweede
mast PQ, ook 4,60 m lang. Die tweede mast kan draaien om punt P, en zit
met kabel SQ vast aan de eerste mast. De lengte x van die kabel
kan men variëren. Op dit moment maakt mast PQ een hoek van 50° met de bodem |
||||
| a. | Bereken de lengte van kabel x op dit moment. | |||
|
||||
| Door de mast PQ eerst zijdelings te draaien en door daarna de lengte van de kabel te veranderen kan men ervoor zorgen dat punt Q van de mast recht boven punt R van een schip komt te liggen. Daarbij is PT = 2 m en TR = 2,5 m. | ||||
| b. | Hoeveel graden moet de mast gedraaid worden, en hoe lang moet de kabel worden zodat Q recht boven R komt te liggen? | |||
|
||||
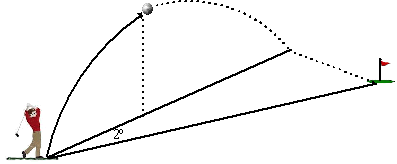
| 8. | Een golfer mikt op een hole die
zich op precies 200 m afstand bevindt Een golfer slaat de bal inderdaad precies 200 m ver weg. Hij slaat de bal echter niet precies in de goede richting, maar (in het bovenaanzicht) met een afwijking van 2º. |
|||
|
|
||||
| Hoe ver komt de bal naast de hole terecht? | ||||
|
||||
| 9. | examenvraagstuk HAVO Wiskunde B, 1994. | |||
| Hieronder zie je vier 'momentopnamen' van het neerlaten van een basketbalstellage. | ||||
|
|
||||
| De stellage bestaat uit een ijzeren
frame met een rechthoekig bord waaraan een basket bevestigd is. Een
basket is een ijzeren ring met een netje. Twee kettingen, die even
lang zijn, dienen als beveiliging tegen vallen of te ver zakken van
het geheel. Het zijaanzicht van dit frame is een parallellogram. |
||||
| We noemen dit
parallellogram ABCD. Zie de figuur hiernaast. BC is 90 cm en AB is 100 cm lang. In de gymzaal waar de foto's genomen zijn, is voor bevestigingspunt B een hoogte van 280 cm gekozen. Neem aan dat een van de kettingen bevestigd is in de punten C en A. Stel dat de ketting zo lang is dat bij het neerlaten van de stellage punt A niet lager kan komen dan 250 cm boven de grond. |
|
|||
| a. | Bereken in dat geval de lengte van de ketting in cm nauwkeurig. | |||
|
||||
| Het frame wordt helemaal omhooggetrokken tot tegen de muur. Tijdens deze beweging beschrijft punt A een baan. De hoogte h van punt A is afhankelijk van β (∠ABC = β). | ||||
| b. | Druk de hoogte h uit in β. Doe dat voor het geval dat A hoger dan B ligt. | |||
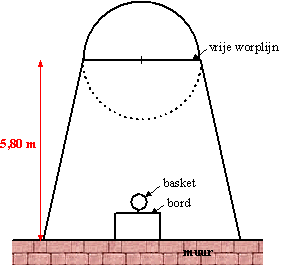
| Hiernaast is een bovenaanzicht getekend van het vrije worpgebied met de basketbalstellage. Het frame wordt zo ver neergelaten dat punt A op een hoogte van 250 cm komt. Neem aan dat het bord met de basket precies even groot is als de voorkant van het frame. Een speler met een ooghoogte van 195 cm staat midden op de vrije worplijn. |
|
|||
| c. | Onderzoek of hij vanaf die plaats boven de rand van het bord iets van het frame kan zien. | |||
| 10. | examenvraagstuk HAVO Wiskunde
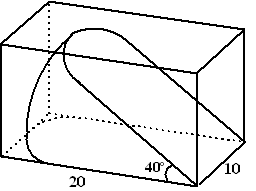
B, 2009. Op foto hieronder zie je drie stukken kaas. Het zijn delen van een hele, ronde kaas. Het grootste stuk is precies de helft van een hele kaas. Deze halve kaas heeft een vlakke zijkant. De vorm van de vlakke zijkant bestaat bij benadering uit een rechthoek van 30 cm bij 10 cm en twee halve cirkels met een diameter van 10 cm. Zie de figuur rechts. |
|||
|
|
||||
| a. | Bereken de oppervlakte van de vlakke zijkant. Rond je antwoord af op een geheel aantal cm2 | |||
|
||||
| Als je verticaal door het midden van de
kaas snijdt, kun je stukken kaas maken zoals die ook op de foto te zien
zijn. Bij een van de stukken kaas op de foto maken de snijvlakken een
hoek van 40° met elkaar.
Zo'n stuk wordt met een snijvlak op de bodem van een balkvormig doosje gelegd. De binnenmaten van het grondvlak van het doosje zijn 20 cm bij 10 cm. |
|
|||
| b. | Bereken hoe hoog de binnenkant van dit doosje minimaal moet zijn om dit stuk kaas er in te laten passen. Geef je antwoord in een geheel aantal centimeters. | |||
|
||||
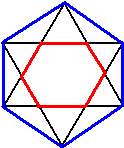
| 11. | Twee
gelijkzijdige even grote driehoeken worden door elkaar heen getekend.
Dat gebeurt zó dat er een symmetrische figuur ontstaat. Bereken de verhouding van de zijden van de rode en de blauwe zeshoek in de figuur hiernaast
|
|
||
|
||||
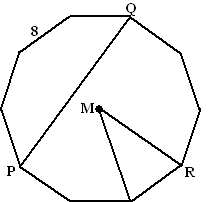
| 12. | Hiernaast
staat een regelmatige tienhoek getekend met zijden 8 en
middelpunt M. Het blijkt dat MR ongeveer gelijk is aan 12,944 |
|
||
| a. | Toon dat aan. | |||
| b. | Bereken PQ in twee decimalen nauwkeurig. | |||
|
||||
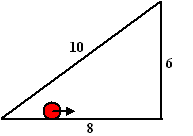
| 13. | Langs
de binnenkant van een driehoek met zijden 6, 8 en 10 rolt een knikkertje
met straal 1, zo dat het steeds contact houdt met een zijde.
Welke afstand heeft het middelpunt M van dat knikkertje afgelegd als het knikkertje precies één keer rondom de driehoek is gerold? |
|
||
|
||||
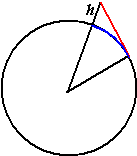
| 14. | Hoe ver kun je op
aarde zien? Neem aan dat de aarde een bol is met straal 6378 km Stel dat je je op hoogte h km boven het aardoppervlak bevindt, en je kijkt via de rode kijklijn hiernaast naar de horizon. Hoeveel kilometer is dan de blauwe afstand? Voor die afstand d geldt: |
|
||
|
|
||||
| a. | Toon dat aan | |||
| b. | Hoeveel kilometer ver kun je vanaf een 100 meter hoge toren kijken? | |||
|
||||
| Voor kleine hoeken
α geldt cosα
≈ 1 - 0,5α2
In dat geval geldt voor de afstand d: |
||||
|
|
||||
| Met R = 6378 km | ||||
| c. | Toon dat aan | |||
| d. | Bereken het verschil in afstand dat deze benadering oplevert voor de afstand uit vraag c) | |||
|
||||
| 15. |
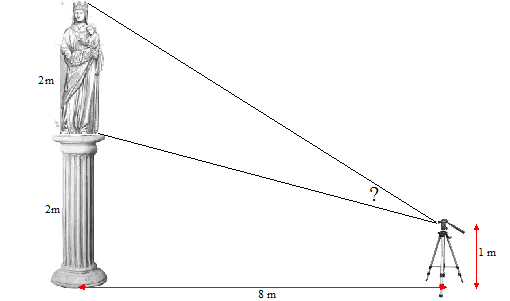
Een standbeeld is 2 meter hoog en staat op een verhoging die ook 2 meter
hoog is. Een fotograaf heeft zijn statief op 8 meter voor het standbeeld
neergezet, en zijn fototoestel bevindt zich op 1 meter boven de grond. De fotograaf wil de hoek waaronder hij het standbeeld ziet graag zo groot mogelijk maken. Hoeveel groter of kleiner wordt die hoek als hij zijn statief één meter dichter bij het standbeeld zet? |
|||
|
|
||||
|
||||
| 16. | Een reuzenrad heeft
een diameter van 12 meter en het laagste punt zit 1 m boven de grond. Bij het instappen zit je dus op een hoogte van 1 meter. Op welke hoogte zit je nadat het rad 50º is gedraaid? |
|
||
|
||||
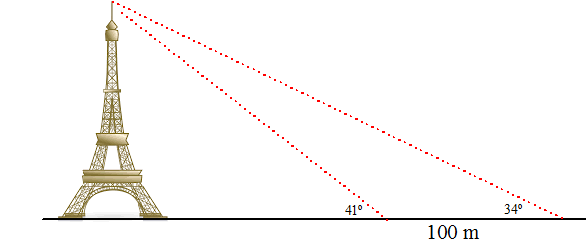
| 17. |
Iemand ziet de Eiffeltoren onder een hoek van
34°. |
|||
|
|
||||
| Hoe hoog is de Eiffeltoren? (Check je antwoord op je mobiel.) | ||||
|
|
||||
|
© h.hofstede (hhofstede@hogeland.nl) |
||||