|
|||||
| 1. | a. | tan35º = 4/x x = 4/tan35º = 5,71 |
|||
| b. | tan28 = x/6 x = 6 • tan28º = 3,19 |
||||
| c. | tan64º = 5/x x = 5/tan64º = 2,44 |
||||
| 2. | a. | tanx = 4/3 x = tan-1(4/3) = 53,1º |
|||
| b. | tanx = 6/2
= 3 x = tan-1(3) = 71,6º |
||||
| c. | tanx = 3/5 x = tan-1(3/5) = 31,0º |
||||
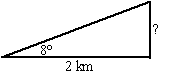
| 3. | tan8º = x/2 x = 2 • tan8º = 0,281 km dus 281 meter |
 |
|||
| 4. | tan6º = 1200/x x = 1200/tan6º = 11417 m dus ongeveer 11,4 km. |
 |
|||
| 5 | a. | cosx = 3/6
= 0,5 x = cos-10,5 = 60º |
|||
| b. | sin32º = 5/x x = 5/sin32º = 9,44 |
||||
| c. | sin15º = x/9 x = 9 • sin15º = 2,33 |
||||
| d. | sinx = 6/7 x = sin-1(6/7) = 59,0º |
||||
| e. | tanx = 6/9 x = tan-1(6/9) = 33,7º |
||||
| f. | cos68º = x/10 x = 10 • cos68º = 3,75 |
||||
| g. | cos20º = 7/x x = 7/cos20º = 7,45 |
||||
| h. | sinx = 5/7 x = sin-1(5/7) = 45,6º |
||||
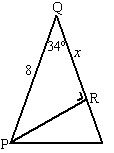
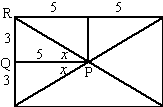
| 6. | a. | trek lijn PQ, die deelt de
gezochte hoek doormidden. in driehoek PQR geldt dan tanx = 3/5 x = tan-1(3/5) = 31º De gevraagde hoek is dan 2 • 31 = 62º |
 |
||
| b. | in driehoek PQR geldt:
cos34º = x/8 x = 8 • cos34º = 6,53 het vraagteken is dan 8 - 6,63 = 1,37 |
|
|||
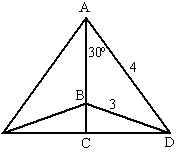
| 7. | trek AB door naar beneden. Dan is
hoek ACD een rechte hoek. in driehoek ACD: cos30º = AC/4 ⇒ AC = 4 • cos30º = 3,46 sin30º = CD/4 ⇒ CD = 4 • sin30º = 2 pythagoras in driehoek BCD: 22 + BC2 = 32 BC2 = 5 ⇒ BC = √5 = 2,24 dan is AB = AC - BC = 3,46 - 2,24 = 1,22 |
|
|||
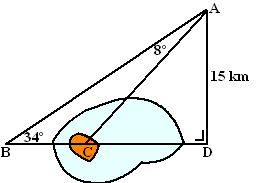
| 8. | ÐBCA
= 180 - 34 - 8 = 138º ÐACD = 180 - 138 = 42º in driehoek ABD: tan34º = 15/BD ⇒ BD = 15/tan34º = 22,24 in driehoek ACD: tan42º = 15/CD ⇒ CD = 15/tan42º = 16,66 BC = BD - CD = 22,24 - 16,66 = 5,58 km |
 |
|||
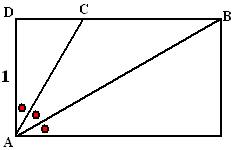
| 9. | elke hoek bij A is
30º in driehoek ACD: tan30º = DC/1 ⇒ DC = tan30º = 0,58 cos30º = 1/AC ⇒ AC = 1/cos30º = 1,15 in driehoek ABD: tan60º = BD/1 ⇒ BD = tan60º = 1,73 dan is BC = BD - CD = 1,73 - 0,58 = 1,15 cos60º = 1/AB ⇒ AB = 1/cos60º = 2 de omtrek is dan AC + BC + AB = 1,15 + 1,15 + 2 = 4,30 |
 |
|||
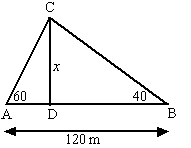
| 10. | Trek CD loodrecht op
AB, en stel dat CD = x in driehoek ACD: tan60º = x/AD ⇒ AD = x/tan60º = x • 1/tan60º = 0,577x in driehoek BCD: tan40º = x/BD ⇒ BD = x/tan40º = x • 1/tan40º = 1,192x AD + BD = 0,577x + 1,192x = 1,769x = 120 dan is x = 120/1,769 = 67,8 m |
|
|||
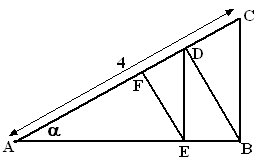
| 11. | als
∠A =
α dan is
∠C = 90 -
α
en dan is ∠CBD =
α
(driehoek BCD) dan is ook ∠DEF = α (F-hoeken met ∠CBD want BD en EF zijn evenwijdig) dan is ook ∠BDE = α (Z-hoeken) in driehoek ABC: sina = BC/4 ⇒ BC = 4sinα in driehoek BCD: cosα = BD/BC = BD/4sinα ⇒ BD = 4sinα • cosα in driehoek BDE: cosα = DE/BD ⇒ DE = BD • cosα = 4sinα • cos2α in driehoek DEF: cosα = EF/DE ⇒ EF = DE • cosα = 4sinα • cos3α |
 |
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||