Recursieformules.

© h.hofstede (h.hofstede@hogeland.nl)
Zin in een spelletje?
Het puzzeltje hiernaast heet de `Torens van Hanoi`.
Het bestaat uit drie houten pinnen met een aantal (in de figuur 8) schijven met een gat in het midden die op de pinnen gelegd kunnen worden. De schijven variëren van groot naar klein. De bedoeling van de puzzel is de hele toren van pin1  naar pin 3 te verplaatsen. Dat moet schijf voor schijf gebeuren, en daarbij is de enige regel: "Er mag nooit een grotere schijf bovenop een kleinere liggen" .

De vraag is: in hoeveel zetten (verplaatsingen van één schijf) kun je dat?
Oefen het eerst een paar keer met steeds meer schijven; in deze applet moet je de schijven naar de rechterpin verplaatsen:
Als het goed is kun je zo'n soort tabel gaan invullen:
aantal schijven 1 2 3 4 5
minimaal aantal zetten 1 3 7 15 ...
Laten we er wat wiskundige notatie in aanbrengen.
Noem u(n) het minimaal aantal benodigde zetten om een toren van n schijven te verplaatsen.
Dus in de tabel zie je dat u(1) = 1 en  u(4) = 15.
De grote wiskunde-prijsvraag is nu natuurlijk:
Kunnen we een formule maken?

En dat kan, maar het wordt wel een aparte formule. De redenering om de formule te vinden is als volgt:
Stel dat ik weet hoe groot un-1 is.
Dan weet ik óók hoe groot un is, kijk maar:
• Ik heb dus een toren met n schijven die van de linker naar de rechterpin moet worden verplaatst
• Verplaats eerst alle schijven behalve de onderste van de linker naar de middelste pin. Dat kost un-1 zetten.
• Verplaats nu de onderste schijf van links naar rechts:  kost 1 zet
• Verplaats tenslotte de toren van n schijven van de middelste naar de rechterpin. Kost weer un-1 zetten
Samen kost dat dus    un-1 + 1 + un-1  = 2un-1 + 1  zetten.
Conclusie: 

un = 2 • un-1 + 1
Daar is onze formule al. Maar het is wel een ander soort formule dan we tot nu toe gewend zijn.
We waren altijd gewend om in een formule een getal (meestal x) in te vullen en direct een uitkomst (meestal y) te krijgen. 
Hier is dat niet zo: als we willen weten hoe groot u10 is kunnen we niet gewoon n = 10 invullen, immers dan staat er u10 = 2 • u9 + 1  en we weten niet hoe groot u9 is!!!! En voor u9 moeten we weer u8 weten.....
Er is maar één oplossing:  om een u-waarde uit te rekenen moeten we stap voor stap alle vorige uitrekenen.
Dat komt natuurlijk omdat de formule alleen aangeeft hoe een u uit de vorige u kan worden berekend. Een formule die dat doet heet een recursieformule:

In een recursieformule wordt aangegeven hoe een getal uit de vorigen kan worden berekend
BELANGRIJK GEVOLG
Gevolg is dat je het eerste getal u1 wel moet weten!! Dat moet erbij worden gegeven. Immers als je alleen maar weet dat un = 2 • un-1 + 1 en niet met welk getal de rij begint, dan kun je niet beginnen te rekenen! 

Oh ja.....nog even iets over de notatie......

We schreven tot nu toe steeds een getal uit de rij als un,  met die n daar onder de u hangend.
Soms zie je ook wel de notatie  u(n).

We noemden het eerste getal uit de rij altijd u1  (of  u(1) natuurlijk).
Vaak wordt het eerste getal ook wel nummer 0 genoemd, dus  u0  of  u(0). Je mag natuurlijk zelf weten hoe je hem noemt, voor mijn part begin je jouw rij met u1250 of zo, maar we zullen later zien dat het wel gevolgen heeft voor formules die we gaan opstellen. Meestal wordt de eerste u0 of u1 genoemd.

Tot slot zijn er nog wel eens mensen die het grappig vinden om een recursieformule te beginnen met un + 1 in plaats van met un. Dat kan natuurlijk. Zo is de formule  un = 2 • un-1 + 1  precies dezelfde als  un + 1 = 2 • un + 1,  immers bij un is  un-1 de vorige en bij un+ 1 is un de vorige.
   
  OPGAVEN
   
1. Bereken u5 van de volgende recursieformules:
         
  a. un = 3 • un-1  + 2   met  u0 = 12.

3158
  b. un = un-12 - 10  met  u0 = 3.

6,3 • 1026
  c. un = 12/u(n-1)   met  u1 = 2.

2
         
2. Stel een recursieformule op bij de volgende rijen getallen.
         
  a. 2 - 5 - 8 - 11 - 14 - 17 - ....

un=un-1+3 met u1=2
  b. 1024 - 512 - 256 - 128 - ....

un = 1/2un-1 met u1=2
  c. 1 - 5 - 13 - 29 - 61 - 125 - ....

un=2un-1+3 met u1=1
  d. 2 - 4 - 16 - 256 - 65536 - ....

un=un-12 met u1=2
         
3. Stel een recursieformule op bij de volgende verhaaltjes.
         
  a. Een kerstboomkweker heeft 1500 bomen. Hij verkoopt elk jaar met kerst 70% van zijn bomen. Direct daarna plant hij elk jaar 800 nieuwe bomen.

un= 0,3un-1 + 300
met u0=800
       
  b. Van alle scholieren die een bepaalde roddel kennen vertelt elke dag 30% die roddel door aan een scholier die hem nog niet kende. Daardoor neemt het aantal scholieren dat de roddel kent snel toe. In het begin kennen 40 mensen de roddel.

un = 1,3un-1
met u1 = 40
       
  c. In een bos zijn 400 konijnen maar hun aantal neemt toe. In de loop van een jaar neemt het aantal konijnen elke keer met 20% toe. Om die enorme groei wat te beperken schiet de boswachter aan het eind van elk jaar 150 konijnen neer.

un = 1,2un-1 - 150
met u1 = 400
         
4. un =  2 •  un-1 - 1  en  het blijkt dat  u5 = 113.  Bereken u1.
       

8
         
5. Een lineaire recursievergelijking van de vorm  un = a • un - 1 + b  levert de volgende waarden op:
         
 
n 0 1 2 3 4
u(n) 10 20 32 46,4 63,68
         
  Bepaal u(6).
       

109,2992
     

 

    
 
Uitbreiding:  un  hangt af van meerdere voorgangers.
De volgende rij is een hele beroemde:
 
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 -........
 

Het is de rij van Fibonacci. Je krijgt een getal uit deze rij door de twee vorigen bij elkaar op te tellen, dus:

 

un = un - 1 + un - 2
 

Gevolg is wel, dat je nu het eerste én het tweede getal moet weten om "op gang te komen" met de rij.
In dit geval is  u1 = u2 = 1.
   
6. In een rij getallen is elk volgende getal gelijk aan het gemiddelde van de twee vorigen.
Geef een recursieformule voor deze rij als hij begint met  10 - 50 - ....
       

un = 0,5(un-1 + un-2)
met u1=10 en u2=50
7. Aan de volgende rij getallen zal je wel niets opvallen:
         
 

0,996  -  0,984  -  0,966  -  0,940  -  0,906  -  0,866  -  ...
         
  Het wordt een stuk duidelijker als je hem zó noteert:
         
 

cos(5) - cos(10) - cos(15) - cos(20) - cos(25) - cos(30) - ....
         
  Voor de cosinus geldt de volgende formule:  cos nx = 2 • cosx • cos(n - 1)x  - cos(n - 2)x
Maak met behulp van deze formule een recursieformule voor de rij bovenaan deze opgave.
         
         
Uitbreiding:  Er staat ook n in de recursieformule.
   
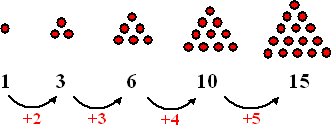
De volgende rij heet de rij van driehoeksgetallen:  1 - 3 - 6 - 10 - 15 - 21 -  ...
Het volgende plaatje maakt duidelijk waarom dat zo is:
   

   
De regelmaat zie je direct als je naar de verschillende tussen de opeenvolgende getallen uit de rij kijkt. Die worden steeds eentje groter. Om bijvoorbeeld u2 te krijgen tel je 2 op bij  u1. Om u3  te krijgen tel je 3 op bij u2. Dus om un te krijgen tel je n op bij un - 1. Dat geeft de volgende recursieformule:
 
un = un-1 + n
 

Zoals je staat er nu behalve een un - 1 ook een n in de formule. Dat kan.
   
8. Hieronder zie je een serie figuren met vierkanten.
         
 

         
  In de eerste figuur zie je 1 vierkant. In de tweede figuur zie je 5 vierkanten! Vier kleine en één grote van 2 bij 2.
         
  a. Tel het aantal vierkanten in de derde en vierde figuur

14 en 30
       
  b. Geef een recursieformule voor het aantal vierkanten in figuur nummer n.
Het eerste vierkant hoort dus bij u1

un = un-1 + n2
         
9. Als je van de functie f(x) = x2 + 2x een tabel met functiewaarden maakt krijg je zoiets:
         
 
x 1 2 3 4 5 6 7
f(x) 3 8 15 24 35 48 63
         
  Als je x ziet als n en f(x) als un dan kun je een recursievergelijking opstellen. Dat lukt omdat er regelmaat in de verschillen tussen de f(x) waarden zit.
Stel zo'n recursievergelijking op.
       

un = un-1 + 2n +1
met u1 = 3
 

© h.hofstede (h.hofstede@hogeland.nl)