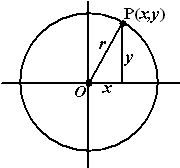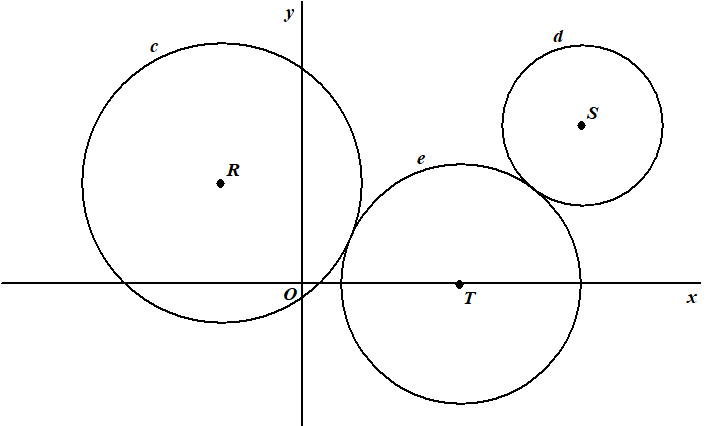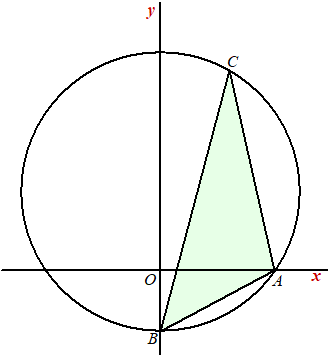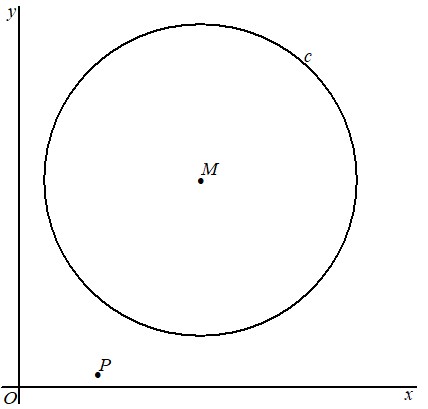|
|
 |
|
De Cirkel. |
ę
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
| De cirkel is zonder enige twijfel
de eenvoudigste en ook mooiste tweedimensionale figuur. Het is de
verzameling van punten met de volgende eigenschap: |
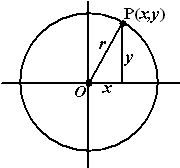 |
| |
|
Een cirkel bestaat uit alle punten met
dezelfde afstand (r) tot een middelpunt (M) |
|
| |
Hiernaast zie je een cirkel met straal r
en middelpunt de oorsprong O. Voor een willekeurig punt P met
co÷rdinaten (x,y) op deze cirkel geldt dan met de stelling van
Pythagoras: x2 + y2 = r2
.
Tadßßßß'! Dat is dus de vergelijking van die cirkel!!! |
| |
|
|
cirkel met middelpunt
O: x2 +
y2 = r2
|
|
| |
|
| En als
het middelpunt niet de oorsprong is?
Nou, dan wordt de grafiek dus verschoven.
Dat gaat zˇ:
Vervang x door (x - a), dan schuift de
figuur a naar rechts.
Vervang y door (y
- a),
dan schuift de figuur a omhoog.
(En met +a wordt dat dan uiteraard naar links/omlaag).
Waarom is dat logisch?
Stel dat het punt P voldoet aan xP2
+ yP2 = r2 en dat
je dat punt a naar rechts schuift. Dan krijg je het punt Q (xQ,
yQ). De vraag is : aan welke vergelijking
voldoen de co÷rdinaten van Q dan?
Omdat het punt a naar rechts is geschoven geldt:
xQ= xP + a en
yQ = yP. Dus xP
= xQ - a en yP =
yQ.
Omdat geldt xP2
+ yP2 = r2 geldt
dus ook (xQ - a)2 + yQ2
= r2 |
| |
|
Het komt er eigenlijk op naar dat
je, als je x vervangt door x - a, een grotere
x nodig hebt om hetzelfde resultaat in je formule te krijgen
(immers voordat je ermee kunt gaan rekenen moet je er eerst a aftrekken).
Een
grotere x betekent: naar rechts!
En voor omhoog/omlaag schuiven geldt precies hetzelfde, maar dan met
y.
Dus geldt in het algemeen voor een cirkel: |
| |
|
|
Cirkel met middelpunt M
en straal r : (x
- xM)2
+ (y -
yM)2
= r2 |
|
| |
|
|
Kwadraat afsplitsen. |
| |
|
De vergelijking hierboven is een
makkelijke. Zo zie je bijvoorbeeld aan de vergelijking (x
-
2)2 + (y + 3)2 = 16 dat het een
cirkel betreft met middelpunt (2, -3) en straal 4. Maar het wordt
lastiger als je een vergelijking krijgt waarin de haakjes zijn
weggewerkt. Dan zou dat in dit geval worden: x2
+ y2 - 4x + 6y
- 3 = 0. De vraag is:
"Hoe vind je dat middelpunt (2, -3) en die straal 4 uit deze
vergelijking?"
Dat kan met een methode die "Kwadraat Afsplitsen" heet, en
dat kun je bestuderen in
deze les. |
| |
|
Voorbeeld. Geef het middelpunt en de straal van de cirkel
x2 + y2 + 4x
- 8y - 20
= 0
x2 + y2 + 4x
- 8y - 20
= 0
⇒ x2 + 4x + 4
- 4 + y2
- 8y + 16 - 16
- 20 = 0
⇒ (x + 2)2
- 4 + (y
- 4)2 - 16
- 20 = 0
⇒ (x + 2)2 + (y
- 4)2
= 40 dus het middelpunt is (-2, 4) en de straal is
√40
Zo vind je altijd het middelpunt en de straal van de cirkel.
Kan er nog iets misgaan?
Jazeker: het zou kunnen dat de r2 die je vindt
negatief is!
In dat geval bestaat de cirkel dus niet. Wiskundigen spreken in
zo'n geval van een imaginaire cirkel. |
| |
|
|
Snijpunten bij cirkels. |
| |
|
Cirkel met rechte lijn.
Het snijpunt van een cirkel met een rechte lijn is vrij makkelijk te
vinden.
Je vult de vergelijking y = ... van de rechte lijn gewoon
in voor de y-en van de cirkelvergelijking.
Kijk maar hoe het werkt:
Voorbeeld.
Bereken de co÷rdinaten van de snijpunten van de lijn y = 2x
- 3 met de cirkel (x + 3)2
+ (y - 1)2 = 100
y = 2x - 3 substitueren geeft (x + 3)2
+ (2x - 3 - 1)2 =
100
⇒ x2 + 6x + 9
+ 4x2 - 16x + 16
- 100 = 0
⇒ 5x2 - 10x
-
75 = 0
⇒ x2
- 2x - 15 = 0
⇒ (x - 5)(x + 3) = 0
⇒ x = 5 ∨
x = -3
Dat geeft de snijpunten (5, 7) en (-3, -9).En
natuurlijk kan het zijn dat de vergelijking die je overhoudt geen
oplossingen heeft (juist: als de discriminant kleiner dan nul is). In
zulke gevallen hebben de cirkel en de lijn gewoon geen snijpunten.
Je raadt het natuurlijk al: dat geeft ons wiskundeleraren de
mogelijkheid om weer leuke sommetjes te verzinnen als: "voor welke
waarden van p snijden de cirkel en de lijn elkaar niet?" |
| |
|
| Cirkel met cirkel. |
| |
|
Dat kan niet zomaar door
substitutie, omdat een cirkelvergelijking nou eenmaal niet te schrijven
is als y = ...... (je zou een vergelijking met
+/- krijgen en bovendien zou die vergelijking nogal vervelende
wortels bevatten).
Maar als je de vergelijkingen van de beide cirkels onder elkaar schrijft
en ze dan van elkaar aftrekt, dan vallen de stukken met x2
en y2 weg!
Dat geeft een lineaire vergelijking en die kun je wÚl schrijven als y
= .....
Als je die dan invult in ÚÚn van beide cirkels, dan kun je toch een
oplossing vinden.
Dat geeft het volgende werkschema:
| |
| Snijpunten van twee cirkels: |
1. schrijf de vergelijkingen zonder
haakjes.
2. trek ze van elkaar af.
3. schrijf het resultaat als y =
... of x = ...
4. substitueer dat in ÚÚn van beide cirkels. |
|
| |
Voorbeeld: Bereken de
co÷rdinaten van de snijpunten van (x
- 3)2
+ (y - 1)2 = 25 en x2
+ y2 + 14x + 8y = 35
Werk de haakjes weg en schrijf ze onder elkaar:
x2 + y2 + 14x + 8y =
35
x2 + y2 - 6x - 2y = 15
Van elkaar aftrekken geeft 20x + 10y = 20
ofwel y = 2 - 2x
Substitueren in bijv. de eerste cirkel: (x
- 3)2
+ (2 - 2x - 1)2 = 25
⇒ x2
- 6x + 9 + 1 -
4x + 4x2 = 25
⇒ 5x2
- 10x - 15 = 0
⇒ x2
- 2x - 3 = 0
⇒ (x + 1)(x
- 3) = 0
⇒ x = -1 ∨
x = 3
Dat geeft vervolgens met y = 2 - 2x de
snijpunten (-1, 4) en (3, -4).
Het snijpunt van twee cirkels kun je ook handig vinden door gebruik te
maken van de zogenaamde machtslijn van de cirkels.
Hoe dat werkt kun je in
deze latere les vinden. Eventjes geduld daarmee dus nog..... |
| |
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Geef de straal en de co÷rdinaten van het
middelpunt van de volgende cirkels: |
| |
|
|
|
| |
a. |
x2 + y2
- 6x
- 10y + 12 = 0 |
|
| |
|
|
|
| |
b. |
x2 + y2 +
2x - 4y = 20 |
|
| |
|
|
|
| |
c. |
3x2 + 3y2
-
9x + 12y = 0 |
|
| |
|
|
|
| |
d. |
x2 + y2
- 23
= 4x + 6y |
|
| |
|
|
|
| 2. |
Voor welke waarden van p
stellen de volgende vergelijkingen cirkels voor? |
| |
|
|
|
| |
a. |
x2 + y2
- 4x
+ 5y = p |
|
| |
|
|
|
| |
b. |
x2 + px + y2
- 6y + 30 = 0 |
|
| |
|
|
|
| |
c. |
3x2 + 6x + py2
- 3y = 0 |
|
| |
|
|
|
| 3. |
Bereken algebra´sch de co÷rdinaten
van de volgende snijpunten: |
| |
|
|
|
| |
a. |
de cirkel (x
- 1)2
+ (y - 2)2 = 13 met de lijn y
= 12 - 2x |
| |
|
|
|
| |
b. |
de cirkel x2
+ y2 + 6x - 2y = 10 met de
lijn y = 3x + 8 |
| |
|
|
|
| |
c. |
de cirkel x2 + 4x
= 29 - y2
- 4y met de lijn
y = -2x + 5 |
|
| |
|
|
|
| 4. |
Welk punten van de lijn
y = 2x + 4 hebben afstand
√10
tot het punt (1,5)? |
| |
|
|
|
| |
|
|
|
| 5. |
a. |
Voor welke waarden van p
snijden de lijn y = 2x + p en de cirkel
x2 + (y - 3)2 = 5
elkaar? |
| |
|
|
|
| |
b. |
Voor welke waarden van p
raakt de lijn y = x + 1 de
cirkel (x - p)2 + y2
= 8 ? |
| |
|
|
|
| |
|
|
|
| 6. |
Bereken algebra´sch de co÷rdinaten
van de volgende snijpunten: |
| |
|
|
|
| |
a. |
De cirkels (x + 5)2
+ (y - 2)2 = 10 en x2
- 2x + y2 = 17 |
| |
|
|
|
| |
b. |
De cirkels x2
+ y2 - 4x = 16 en x2
+ y2 = 8x + 8y
- 24 |
| |
|
|
|
| |
c. |
De cirkels x2
+ y2 = 2x - 2y + 8 en
(y + 4)2 = 8x
- x2
- 12 |
| |
|
|
|
| |
|
|
|
| 7. |
Gegeven zijn de twee cirkels
x2 + y2 - 6x
- 4y
= 12 en x2 + y2
+ 12x - 28y = p |
| |
|
|
|
| |
 a. a. |
Bereken algebra´sch voor welke p
deze cirkels elkaar raken. |
| |
|
|
|
| |
Je kunt deze vraag ook op een andere
manier beantwoorden, namelijk door je te realiseren dat als twee
cirkels elkaar raken, dat dan het raakpunt altijd ligt op de
verbindingslijn van beide middelpunten. |
| |
|
|
|
| |
b. |
Gebruik die verbindingslijn om vraag a) nogmaals te beantwoorden. |
| |
|
|
|
| 8. |
Examenvraagstuk HAVO Wiskunde B,
2017-II |
| |
|
|
|
| |
De cirkel c met middelpunt R is
gegeven door (x -
4)2 +
( y
-
5)2 =
49 en
de cirkel d met middelpunt S is gegeven door (x
- 14)2 +
( y
- 8)2 = 16
.
Een derde cirkel e, met middelpunt T op de x-as,
raakt aan beide cirkels.
Verder liggen c en d buiten e. Zie de figuur. |
| |
|
|
|
| |
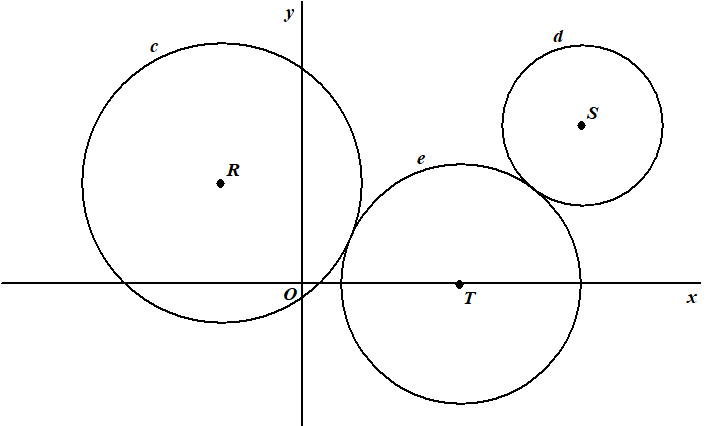 |
| |
|
|
|
| |
De x-co÷rdinaat van T noemen we p,
dus OT =
p .
Er geldt: de afstand van R tot T is gelijk aan
√(p2 + 8p
+ 41) |
| |
|
|
|
| |
a. |
Bewijs dit. |
|
| |
|
|
|
| |
De lijn door R en T gaat door het
raakpunt van de cirkels c en e.
Bovendien gaat de lijn door S en T door het raakpunt
van de cirkels d en e.
Verder is de afstand van S tot T gelijk aan √(
p2 -
28p +
260) . |
| |
|
|
|
| |
b. |
Bereken de straal van cirkel e. |
| |
|
|
|
| |
|
|
|
| 9. |
Examenvraagstuk VWO Wiskunde B, 2017-II (gewijzigd)
In een assenstelsel liggen de punten A(4, 0)
en B(0,
-2)
op de cirkel met vergelijking x2
+
( y
-
3)2
=
25 .
We bekijken in deze opgave driehoeken ABC met punt C
op de grote cirkelboog AB. Zie de figuur. |
| |
|
|
|
| |
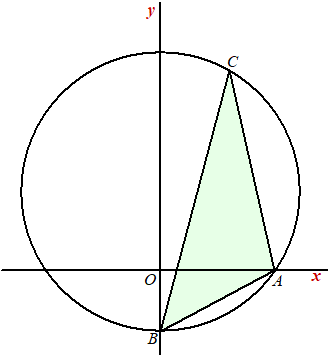 |
| |
|
|
|
| |
Er zijn twee plaatsen van C op de cirkel
waarbij driehoek ABC een rechthoekige driehoek is. |
| |
|
|
|
| |
a. |
Bereken exact van deze twee
plaatsen de co÷rdinaten van C. |
| |
|
|
|
| |
Voor een bepaalde plaats van C op de cirkel
is driehoek ABC een gelijkbenige driehoek met top A,
dus met AB
=
AC |
| |
|
|
|
| |
b. |
Bereken exact de co÷rdinaten van C
waarvoor dat het geval is. |
| |
|
|
|
| 10. |
Examenvraagstuk Havo, Wiskunde B, 2018.
De cirkel
c
met middelpunt
M
is gegeven door x2 + y2
- 28x
- 32y = -308
In de figuur zijn punt
P
en cirkel
c
met middelpunt
M
weergegeven. |
| |
|
|
|
| |
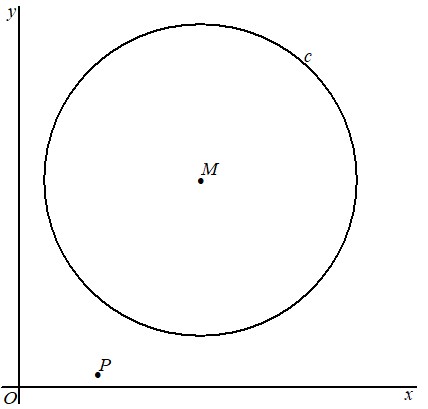 |
| |
|
|
|
| |
De afstand tussen c en P is 5.
De afstand tussen M en P is groter dan de afstand
tussen M en de x-as.
Bereken exact het verschil tussen deze twee
afstanden. |
| |
|
|
|
 |
|
| |
|
|
 |
|
ę
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|