 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
Macht van een punt ten opzichte van
een cirkel. |
| |
|
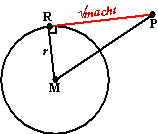
De macht van een punt P ten
opzichte van een cirkel c met straal r en middelpunt M
is gedefinieerd als PM2 - r2
In de figuur hiernaast zie je heel eenvoudig dat die macht gelijk is aan
het kwadraat van de lengte van lijnstuk PR dat de cirkel raakt. Als het
punt P op de cirkel ligt is PM2 = r2 dus is
de macht nul. Ligt het punt binnen de cirkel dan is de macht ervan
negatief. |
 |
| |
• Binnen de cirkel: macht
negatief
• Op de cirkel: macht nul
• Buiten de cirkel: macht positief |
|
| |
|
|
| De macht van een punt varieert dus van -r2
(als P = M) tot oneindig groot (als P oneindig ver weg ligt). |
| |
|
Een formule ervoor..
Laten we er een formule voor gaan maken.
Neem een cirkel met middelpunt M(a, b) en
straal r. Neem verder een punt P(xP, yP)
waarvan we de macht gaan berekenen.
Stel dat PR de cirkel raakt in punt R. Eigenlijk zoals in de
tekening hierboven dus.
Nu is PM = Ö((xP
-
a)2 + (yP - b)2)
en MR = r
Dus de macht is PM2 - r2 =
(xP
- a)2 +
(yP - b)2
- r2
Maar hé.... Wacht eens even.......
Daar in het rood staat gewoon precies (op nul herleid, dat wel) de
vergelijking van de cirkel!! Het enige is dat in plaats van x en
y nu de xP en yP
van het punt P waarvan we de macht wilden berekenen zijn gebruikt!!
| |
Macht van P berekenen?
• Herleid de cirkelvergelijking op nul
• Vul de coördinaten van P in. |
|
| |
|
| |
|
Voorbeeldjes.
• Bereken de macht van punt P(4,6) ten opzichte van cirkel
x2 + 2x + y2 - 6y
+ 12 = 0
Nou, gewoon 42 + 2 •
4 + 62 - 6 • 6 + 12 = 36
• Bereken de macht van P(-2,
5) ten opzichte van de cirkel (x - 2)2 = 6x
- (y + 3)2 + 10
Herleiden op nul: (x - 2)2
- 6x
+ (y + 3)2 - 10 = 0
Invullen: (-2 - 2)2
- 6 •
-2 + (5 + 3)2 - 10 = 82 |
| |
|
|
Goed... Wat kunnen we d'r mee? |
| |
|
1. Cirkels die elkaar loodrecht
snijden.
Zoals je hiernaast ziet, is in zo'n geval de straal van de ene cirkel in
het kwadraat gelijk aan de macht van het middelpunt ten opzichte van de
andere cirkel.
| |
| r12
= macht van M1 tov. c2
|
|
| |
|
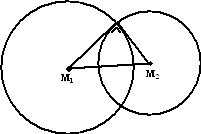 |
Voorbeeld. Geef een vergelijking van de cirkel met
middelpunt (2,6) die de cirkel x2 + y2
- 5x + 2y = 10 loodrecht snijdt.
De macht van (2,6) t.o.v. de gegeven cirkel is gelijk aan 22
+ 62 - 5 • 2 + 2 • 6
- 10 = 32
De cirkel heeft dus straal √32 en middelpunt
(2,6) dus het is (x - 2)2 + (y
- 6)2
= 32 |
| |
|
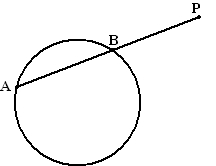
2. Een lijnstuk in stukken
verdelen.
Zie de figuur hiernaast waar een koorde AB van een cirkel is verlengd
naar punt P.
Dan geldt:
Dat betekent dus dat voor alle lijnstukken die je vanaf P naar een
punt A van de cirkel tekent geldt dat AP • PB hetzelfde is! |
 |
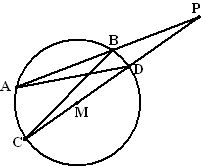
Het bewijs van deze stelling is eenvoudig in te zien door een hulplijn
van P door het middelpunt van de cirkel te tekenen.
Dan geldt ∠DCB = ∠DAB
want beiden zijn de omtrekshoek van boog BD.
Dus zijn de driehoeken APD en CPB gelijkvormig.
⇒ AP/PD = CP/PB
⇒ AP • PB = CP • PD = (PM + r)(PM
- r) = PM2
- r2 = macht van punt P. |
 |
| |
|
| |
|
|
|
| 1. |
Geef een vergelijking van de cirkel met
middelpunt (-2,-10) die de cirkel x2 +
y2 + 2x + y = 16
loodrecht snijdt. |
| |
|
|
|
x2
+ y2 + 4x + 20y + 30
= 0 |
|
| |
|
|
|
| 2. |
Toon aan dat de cirkels x2
+ y2 - 2x + 2y = 18 en
x2 + y2 - 16x + 34 =
0 elkaar loodrecht snijden. |
| |
|
|
|
| 3. |
Een cirkel met straal 10 en middelpunt op de
y-as snijdt de cirkel x2 + y2
+ 12x - 3y + 12 = 0 loodrecht.
Bereken de coördinaten van het middelpunt van de cirkel. |
| |
|
|
|
| |
|
|
|
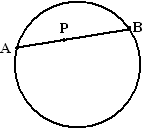
| 4. |
Voor een lijnstuk AB binnen
een cirkel, waarop een punt P ligt geldt:
PA • PB = macht van punt P (maar dan wel positief genomen).
Het bewijs daarvan gaat op dezelfde manier als het bewijs bij
een punt buiten de cirkel.
Geef dat bewijs. |
 |
| |
|
|
|
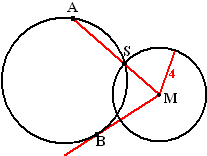
| 5. |
Twee cirkels, waarvan c1
straal 4 en middelpunt M heeft, snijden elkaar in S.
MS snijdt cirkel c2 ook nog in punt A.
MB is een raaklijn aan c2.
Bereken de lengte van MB als gegeven is dat MA = 9. |
 |
| |
|
|
|
|
| |
|
|
De machtlijn van twee cirkels. |
| |
|
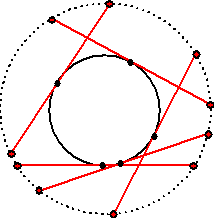
Waar liggen alle punten die dezelfde macht
hebben ten opzichte van een gegeven cirkel?
Hiernaast staat een cirkel met straal 2 en daarbij allemaal punten
waarvan de macht 3 is getekend. Het zijn de rode stippen. 't Is alsof
een lijnstuk met lengte 6 over de buitenkant van de cirkel rolt waarbij
het midden de cirkel blijft raken.
De tekening doet ons vermoeden dat al die punten met dezelfde macht wéér
op een cirkel liggen, met hetzelfde middelpunt als de oorspronkelijke.
(Het feit dat dit een volledig symmetrisch probleem is doet ons dat
trouwens óók vermoeden).
Het bewijs van dit vermoeden is erg simpel. Kijk maar: |
 |
Neem aan dat de cirkel middelpunt
(a, b) heeft en straal r. Laten we aannemen dat we
de punten P(x, y) zoeken die allemaal macht m ten
opzichte van deze cirkel hebben.
Dan geldt voor die punten: m = PM2
- r2
= (x - a)2 + (y
- b)2
- r2
Daaruit volgt dat (x - a)2 + (y
-
b)2 = r2 + m
En jawel! Dit is weer een cirkel, met inderdaad het zelfde
middelpunt, en met straal √(r2
+ m). |
| |
|
Volgende
probleem: Stel dat we twee cirkels hebben, waar
liggen dan de punten waarvoor de macht ten opzichte van beide cirkels
gelijk is?
Nou, dat geeft dan natuurlijk een serie cirkels. Hieronder zie je voor
twee zwarte cirkels met straal 2 en 1,5 de cirkels met macht 2, 4,
8, en 16 getekend. Zelfde kleur is zelfde macht. |
| |
|
|
 |
| |
|
| De punten die dezelfde macht ten
opzichte van beide cirkels hebben zijn dan natuurlijk de
snijpunten van cirkels met dezelfde kleur. Je ziet dat die netjes op een
rechte lijn liggen. Die lijn heet de machtlijn
van beide
cirkels.
Laten we dit vermoeden meteen maar even bewijzen:
| |
Neem cirkel 1: x2
+ y2 + ax + by + c = 0
en cirkel 2: x2 + y2
+ ex + fy + g = 0
Om de macht van een punt P(x, y) te
vinden moest je de coördinaten van dat punt invullen in de
vergelijking van de cirkel.
Als P(x,y) ten opzichte van beide cirkels dezelfde
macht heeft, dan moet dus gelden:
x2 + y2 + ax + by
+ c = x2 + y2 + ex
+ fy + g
daaruit volgt: x(a
- e) +
y(b - f) + (c
- g) = 0
Dat is inderdaad een rechte lijn. |
| q.e.d. |
|
Het zal je hopelijk (uit symmetrie-overwegingen) niet verbazen dat
die machtlijn loodrecht op de verbindingslijn van beide middelpunten
staat.
Vooruit, ook maar even bewijzen:
| |
Neem cirkel 1: x2
+ y2 + ax + by + c = 0
en cirkel 2: x2 + y2
+ ex + fy + g = 0
Dan zijn de middelpunten (-1/2a
, -1/2b) en (-1/2e,
-1/2f) en de lijn daartussen
heeft helling (f - b)/(e
- a)
De machtlijn had vergelijking x(a - e)
+ y(b - f) + (c - g) = 0 en die
heeft helling (e
- a)/(b
- f)
Als je deze twee hellingen met
elkaar vermenigvuldigt levert dat -1 op, dus staan beide lijnen
loodrecht op elkaar. |
| q.e.d. |
|
Conclusies:
| |
De machtlijn van
x2 +
y2 + ax + by + c
= 0 en x2 +
y2 + ex + fy + g = 0
is de lijn x(a
-
e) + y(b
- f) + (c
- g)
= 0
Die staat loodrecht op de verbindingslijn van de
middelpunten. |
|
| |
Als de twee cirkels elkaar snijden, dan is het nog eenvoudiger: de
snijpunten van beide cirkels hebben macht nul ten opzichte van beide
cirkels, dus liggen ze op de machtlijn. De machtlijn moet dan wel de
lijn door de snijpunten zijn.
En als de cirkels elkaar raken, dan gaat de machtlijn door het raakpunt,
en omdat hij loodrecht op de verbindingslijn van de middelpunten staat
moet het wel de gemeenschappelijke raaklijn zijn.
| |
• De machtlijn van twee snijdende cirkels is de
lijn door beide snijpunten
• De machtlijn van twee rakende cirkels is de
gemeenschappelijke raaklijn. |
|
| |
Deze laatste eigenschap heb je in feite al eerder gebruikt toen je de
snijpunten van twee cirkels uitrekende:
Voorbeeld:
Bereken de snijpunten van de cirkels x2 + y2
- 4x + 6y = 52 en x2 +
y2 - x + 2y = 41
De machtlijn van beide cirkels is de lijn -3x + 4y =
11, ofwel y = 0,75x + 2,75
Invullen in de eerste cirkel: x2 +
(0,75x + 2,75)2 - 4x + 6(0,75x + 2,75) =
52
⇒ x2 + 0,5625x2
+ 4,125x + 7,5625 - 4x + 4,5x + 16,5 = 52
⇒ 1,5625x2 + 4,625x
- 27,9375 = 0
⇒ x = 3 en dan is y
= 5. Kennelijk raken de cirkels elkaar in (3,5).
Voorbeeld.
Gegeven zijn de cirkels c1: x2
+ 4x + y2 = 15 en c2:
x2 + y2 - 8x +
2y = 20
Cirkel c3 heeft middelpunt op de
x-as en snijdt beide cirkels c1 en c2
loodrecht.
Geef de coördinaten van het middelpunt M3 van c3.
Als cirkel c3 beide cirkels loodrecht snijdt, dan is
de macht van M3 ten opzichte van c1
gelijk aan r3, en ook de macht van M3
ten opzichte van c2 is gelijk aan r3
M3 heeft dus gelijke macht ten opzichte van beide cirkels,
dus ligt M3 op de machtlijn.
De machtlijn is de lijn 12x - 2y + 5 = 0
Als M op de x-as ligt is yM = 0
dus 12x + 5 = 0 ⇒ xM
= -5/12
dus M is het punt (-5/12,
0). |
| |
|
| |
|
|
|
| 6. |
Gegeven zijn de cirkels c1:
x2 + y2 = 12 en c2:
x2 + y2 + 6x =
10
Punt P heeft macht 4 ten opzichte van c1 en
macht 6 ten opzichte van c2.
Geef de coördinaten van P. |
| |
|
|
|
| 7. |
Neem drie cirkels waarvan de middelpunten niet
op één lijn liggen en niet samenvallen.
Dan geldt de volgende stelling: |
| |
|
|
|
| |
| De machtlijnen van deze drie cirkels gaan
door één punt. |
|
| |
|
|
|
| |
a. |
Toon aan dat de machtlijnen van deze
cirkels elkaar snijden als de middelpunten niet op één lijn
liggen en niet samenvallen.. |
| |
|
|
|
| |
Stel dat punt P het snijpunt is van
de machtlijnen m12 en m13
(de machtlijnen van c1c2
en van c1c3). |
| |
|
|
|
| |
b. |
Toon aan dat P dan ook op de
machtlijn van c1 en c2 ligt.
Leg uit hoe daaruit bovenstaande stelling volgt. |
| |
|
|
|
| |
c. |
Hieronder zie je twee cirkels c1
en c2.
Gebruik bovenstaande stelling om de machtlijn van deze twee
cirkels te construeren. Doe dat door een derde willekeurige
cirkel c3 te tekenen die beide gegeven cirkels
snijdt. |
| |
|
|
|
| |
|
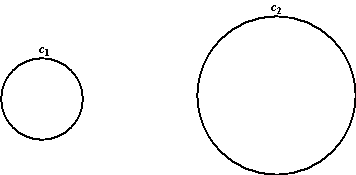 |
| |
|
|
|
| |
d. |
Neem een willekeurige driehoek ABC.
Teken drie cirkels met steeds een zijde van deze driehoek als
middellijn.
Toon met bovenstaande stelling aan dat de drie hoogtelijnen van
een driehoek door één punt gaan. |
| |
|
|
|
| 8. |
Gegeven zijn de cirkels c1:
x2 + y2 = 13 en
c2: x2 + y2
+ 4x - 2y = 12
A(2, 3) is een punt van c1.
Stel een vergelijking op van de cirkel door A die c1
en c2 loodrecht snijdt. |
| |
|
|
|
| |
TIP: |
| M3 ligt op de
raaklijn aan c1 in A |
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|