Nieuwe pagina 1

Epidemie.

Men spreekt van een epidemie als in korte tijd minstens 2% van de bevolking een besmettelijke ziekte oploopt. Een voorbeeld van zo’n ziekte is griep. Rond 1930 hebben twee Schotse wiskundigen, Reed en Frost, epidemieën bestudeerd. Zij hebben de wetmatigheden die zij daarbij meenden te zien in een wiskundig model vastgelegd. Met dit model kan men voorspellingen doen over de aantallen zieken na het uitbreken van een epidemie. Deze opgave gaat over verschillende varianten van dit zogeheten Reed-Frost-model. In de modellen die we hier bekijken, kunnen mensen vatbaar, ziek of immuun zijn. Wie vatbaar is, kan ziek worden. Dat gebeurt uitsluitend wanneer je in contact komt met een zieke en daarbij besmet raakt. Wie ziek is, geneest na verloop van tijd. Bij sommige ziekten kan hij of zij dan opnieuw vatbaar worden, bij andere ziekten wordt hij of zij dan immuun. Wie immuun is of wordt, blijft immuun en kan voorlopig niet meer ziek worden. In deze opgave gaat het steeds over een populatie van 10 000 mensen. We beschrijven de ontwikkeling van de aantallen mensen die vatbaar, ziek of immuun zijn met stappen van een week. In week n zijn er V_n mensen vatbaar, Z_n mensen ziek en I_n mensen immuun. Voor elke week geldt: V_n + Z_n + I_n = 10 000. We beginnen met week 0. We nemen in deze opgave steeds aan dat er 10 mensen ziek zijn in week 0. Als nog niemand immuun is, geldt dus Z₀ = 10; I₀ = 0; V₀ = 9 990. We bekijken een ziekte waarbij iedere zieke na één week genezen is en dan immuun wordt. We krijgen dan de volgende recurrente betrekkingen: • Z_{n + 1} = (1 - k^Zn)V_n • I_n₊₁= I_n + Z_n • V_n₊₁ = 10 000 − Z_n₊₁ − I_n₊₁ Hierbij is k een getal tussen 0 en 1, dat aangeeft in welke mate er binnen de populatie van 10 000 mensen besmetting plaatsvindt: bij k = 1 is er geen besmetting en bij k = 0 zal iedere vatbare ziek worden. Om het model bij de werkelijkheid te laten aansluiten beperken we ons tot waarden van k die dicht bij 1 liggen.

	Open het Excel-bestand ‘EPIDEMIE-1.XLS’.

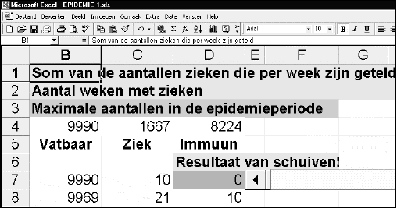
Deze spreadsheet is gemaakt op basis van bovenstaande recurrente betrekkingen, alleen worden de aantallen elke week afgerond op gehele getallen. Er wordt echter wel doorgerekend met niet-afgeronde waarden. Wanneer je het bestand opent, geldt I₀ = 0 en k = 0,99979.



Op het scherm zie je per week hoeveel mensen er vatbaar, ziek en immuun zijn. Deze aantallen staan in de kolommen B, C en D.



De aantallen voor week 1 tot en met 24 staan ook in het staafdiagram. Je ziet dat in week 9, op het hoogtepunt van de epidemie, 1667 mensen ziek zijn. Als de epidemie voorbij is, zijn er 8224 mensen immuun. Die zijn allemaal ziek geweest en genezen. De maximale aantallen vatbaren, zieken en immunen in een week van de epidemieperiode staan in rij 4 van de spreadsheet. Let op: Bijvoorbeeld in week 4 zijn de drie aantallen vatbaren, zieken en immunen samen niet 10 000, maar 10 001. Dat komt door het afronden op gehele getallen. Verder zie je een schuifbalk voor een factor g.



De schuifbalk staat op 1 en moet voorlopig op 1 blijven staan. Op deze factor komen we later terug. In de spreadsheet kun je de aantallen vatbaren, zieken en immunen van week 12 aflezen.

5p.	1.	Laat met een berekening zien dat je met de bovenstaande recurrente betrekkingen uit deze waarden van week 12 inderdaad die in week 13 kunt berekenen.

Door tijdig mensen te vaccineren kan men zorgen dat al bij het uitbreken van de ziekte een aantal mensen immuun is. Dit aantal is I₀. Om het effect van vaccinatie te bestuderen kun je op het scherm I₀ veranderen. Dat kan door op de plaats van I₀ een getal in te tikken en dan op Enter te drukken, of door te schuiven met de schuifbalk die ernaast staat. Voor de economie is het belangrijk dat er niet te veel zieken zijn. Door voldoende mensen te vaccineren kan men zorgen dat het aantal zieken per week nooit boven de 1000 komt.

2p.	2	Onderzoek hoeveel mensen er ten minste gevaccineerd moeten worden om te zorgen dat het aantal zieken per week nooit boven de 1000 komt.

Tot nu toe gingen we ervan uit dat iedere zieke na één week genezen is. Bij veel ziekten geldt dat de genezing niet bij iedereen even lang duurt. We gaan er nu van uit dat elke week slechts een fractie g (g een getal tussen 0 en 1) van de zieken de daaropvolgende week genezen is (en dus immuun wordt). De recurrente betrekkingen van het model moeten hieraan worden aangepast. De formules voor Z_n₊₁, V_n₊₁ en I_n₊₁ worden dan: • Z_n_{+ 1} = (1 - k^Zn) · V_n + (1 - g) · Z_n • I_n₊₁ = I_n + g · Z_n • V_n₊₁ = 10 000 − Z_n₊₁ - I_n₊₁ Hierin is de formule voor V_n₊₁ ongewijzigd gebleven. Ga op het scherm terug naar de situatie waarin er niet ingeënt wordt: I₀ = 0. Neem k = 0,99979 en g = 1. Door middel van de schuifbalk kan g veranderd worden (niet door een getal in te tikken!). Voor iedere waarde van g geldt dat wie ziek wordt, gemiddeld ongeveer ¹/_gweken ziek is. Dus als bijvoorbeeld g = 0,5 dan zijn de mensen die ziek worden, gemiddeld 2 weken ziek. Bij g = 0,25 zullen de mensen gemiddeld 4 weken ziek zijn. Omdat we ervan uit gaan dat er nu niet ingeënt wordt (I₀ = 0), zal het totaal aantal mensen dat ziek is geweest, op het eind gelijk zijn aan het getal in D4. Als je van iedere week het aantal zieken kent en deze aantallen optelt, krijg je het getal in I1.

4p.	3.	Bereken voor g = 0,2 en g = 0,1 de uitkomst van de deling ^I1/_D4 en leg uit wat deze uitkomsten betekenen.

Model 2 Er zijn ook ziekten waarvoor je niet immuun wordt. Bij dergelijke ziekten is dus I_n = 0 voor elke n. Iemand die genezen is, is direct weer vatbaar en kan opnieuw ziek worden. Als we veronderstellen dat iedereen na één week ziekte weer beter is (dus g = 1), dan krijgen we de volgende recurrente betrekkingen: • Z_{n + 1} = (1 - k^Zn) · V_n • V_n₊₁ = 10000 − Z_n₊₁ We gaan bij dit model 2 weer uit van de beginwaarden Z₀ = 10 en V₀ = 9990. Doordat er geen immuniteit optreedt, kan een epidemie een heel ander verloop krijgen dan bij model 1.

	Open het Excel-bestand ‘EPIDEMIE-2.XLS’.
Deze spreadsheet hoort bij model 2. Wanneer je het bestand opent, geldt k = 0,99979. Je ziet in kolom C dat het aantal zieken toeneemt tot 3362 en dan constant blijft. Dit is een opmerkelijk verschil met model 1 (met immuniteit), waar op den duur niemand meer ziek was. Afhankelijk van de waarde van k kunnen in dit model 2 drie situaties ontstaan. Het aantal zieken: • stijgt naar een evenwichtswaarde (zoals je bij k = 0,99979 op het beeldscherm ziet), • daalt naar 0 of • gaat schommelen rond een evenwichtswaarde.

4p.	4.	Geef bij de tweede mogelijkheid (het aantal zieken daalt naar 0) en bij de derde mogelijkheid (het aantal zieken gaat schommelen rond een evenwichtswaarde) een voorbeeldwaarde van k.

We bekijken de situatie waarin het aantal zieken nadert naar een evenwichtswaarde.

4p.	5.	Onderzoek of deze evenwichtswaarde groter dan 5000 kan zijn. Licht je antwoord toe met een redenering.

Webgrafieken bij model 2 Uit bovenstaande recurrente betrekkingen voor model 2 kan een betrekking worden afgeleid waar alleen het aantal zieken en niet het aantal vatbare personen in voorkomt. Deze betrekking luidt: • Z_n_{+ 1} = (1 - k^Zn) (10000 - Z_n)

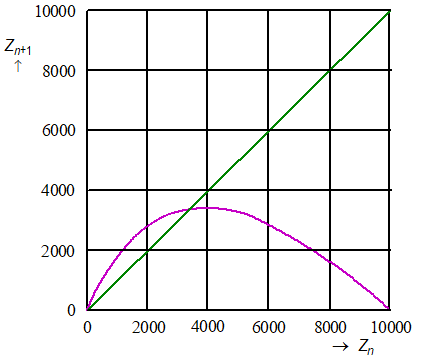
Hiernaast zie je de grafiek van het verband tussen Z_n en Z_n₊₁ getekend voor k = 0,99979. De hierboven genoemde evenwichtswaarde 3362 vind je in deze grafiek terug bij het snijpunt van de grafiek met de diagonale lijn.

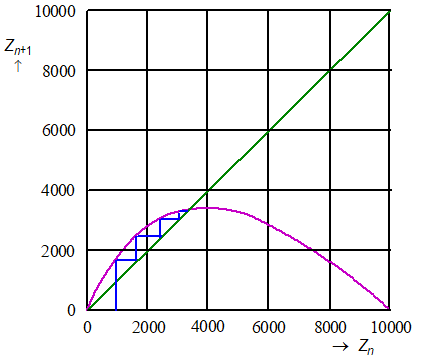
4p.	6.	Teken in de figuur de eerste vier stappen van de webgrafiek (dus voor n = 0 tot en met n = 4). Neem Z₀ = 1000.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

1.

2.

3.

4.

5.

6.

VWO WA12, 2003 - I COMPEX